Poniedziałek 800
Wydział Górniczy |
Imię i nazwisko: 1. Lucyna Szostok 2. Angelika Trawińska |
Rok:
II |
Grupa:
IV |
Nr zespołu:
4 |
|||
Pracowania fizyczna I |
Temat: Wahadła fizyczne. |
Nr ćwiczenia: 1 |
|||||
Data wykonania: 08.11.99. |
Data oddania: 15.11.99. |
Zwrot do poprawy: |
Data oddania: |
Data zal.: |
Ocena: |
||
1.Cel ćwiczenia.
Zapoznanie się z ruchem drgającym wahadła fizycznego. Wyznaczenie momentu bezwładności brył sztywnych przez pomiar okresu drgań.
2. Wprowadzenie teoretyczne.
Wahadłem fizycznym nazywamy dowolne ciało sztywne zawieszone tak, że może się wahać dookoła pewnej osi przechodzącej przez to ciało.
Przykład takiego ciała został narysowany poniżej:
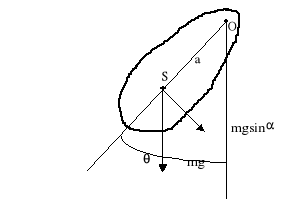
Jest to bryła sztywna o masie m., środku ciężkości w punkcie S, zawieszona w punkcie O, wychylona o kąt θ. Puszczona swobodnie, będzie wykonywać drgania zwane ruchem wahadłowym. Jest to obrót bryły sztywnej wokół osi O pod wpływem momentu siły ciężkości. Dla wychylenia θ moment tej siły jest równy M= mgasinθ ( skierowany przeciwnie do kierunku wychylenia). Według II zasady dynamiki dla ruchu obrotowego iloczyn momentu bezwładności I i przyspieszenia kątowego jest równy działającemu momentowi siły. Moment bezwładności można również wyznaczyć z zależności opisujących ruch wahadła fizycznego:
![]()
gdzie:
a - odległość środka masy od osi obrotu ,
m - masa bryły,
- moment bezwładności względem osi obrotu.
Każdą bryłę sztywną o masie m, zawieszoną w punkcie O różnym od środka ciężkości , można uważać za wahadło fizyczne. Wahadło odchylone od pionu o kąt , a następnie puszczone swobodnie, będzie wykonywać drgania zwane ruchem wahadłowym. Mamy tu zatem do czynienia z obrotem bryły sztywnej wokół osi O pod wpływem momentu siły ciężkości
![]()
, gdzie ![]()
Rozwiązaniem tego równania jest ruch harmoniczny prosty :
![]()
gdzie amplituda i faza zależą od warunków początkowych. Okres drgań T, związany
bezpośrednio z częstotliwością wynosi :
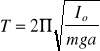
Moment bezwładności względem środka ciężkości S, można obliczyć stosując twierdzenie Steinera:
Io = Is + m.a2
Bryłę sztywną można traktować jako ciągły zbiór punktów materialnych o różnych odległościach od osi obrotu. Moment bezwładności można zatem wyliczyć ze wzoru:
![]()
gdzie r jest odległością elementu masy dm od osi obrotu.
3.Wyniki pomiarów i obliczeń:
wyznaczanie momentu bezwładności pręta.
Dane:
waga pręta m=755 [g]=0,755 [kg], Δm=0,1 [g]=0,0001 [kg]
długość l=79,5 [cm]=0,795 [m], Δl=0,1 [mm]=0,0001 [m]
odległość od środka ciężkości do osi obrotu a=30 [cm]=0,3 [m], Δa=0,1 [mm]=0,0001 [m]
przyspieszenie ziemskie g=9,81 [m/s2]
Lp. |
Czas t [s] |
t/40 |
1 |
54,47 |
1,36 |
2 |
54,42 |
1,36 |
3 |
54,25 |
1,36 |
4 |
54,25 |
1,36 |
5 |
54,22 |
1,36 |
6 |
54,38 |
1,36 |
7 |
54,47 |
1,36 |
8 |
54,69 |
1,37 |
9 |
54,00 |
1,35 |
10 |
54,96 |
1,37 |
![]()
Wartość średnia czasu 40 wahnięć wynosi:
Wartość czasu jednego okresu wynosi:
![]()
Błąd ΔT obliczamy następująco:
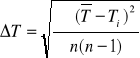
ΔT=2,11.10-3 [s]
Moment bezwładności I0 pręta wyznaczamy z wzoru:
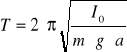
Po przekształceniach otrzymujemy:
![]()
gdzie:
m=755.10-3 [kg],
a=0,30 [m],
g=9,81 [m/s2].
Moment bezwładności wynosi:
I0=104,89.10-3 [kg.m2]
Z prawa przenoszenia błędów wyznaczamy błąd momentu bezwładności:
![]()
= 0,33.10-3 [kg.m2]
gdzie : ΔT= 2,11.10-3 [s]
![]()
![]()
![]()
Procentowy błąd przy obliczaniu momentu bezwładności:
δ=0,31 [%].
Wykorzystując tw. Steinera :
![]()
wyznaczamy moment bezwładności względem środka ciężkości:
![]()
gdzie:
I0=104,89.10-3 [kg.m2]
m=755.10-3 [kg],
a=0,30 [m],
![]()
Obliczenie błędu dla IS z prawa przenoszenia błędów:
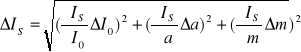
gdzie:
ΔI0=0,33.10-3 [kg.m2]
Wartość ΔIS= 0,32 .10-3 [kg.m2]
![]()
Procentowy błąd momentu bezwładności:
δ=0,86 [%].
Obliczenie wartości momentu bezwładności IS na podstawie zmierzonych wartości masy i wymiarów geometrycznych:
waga pręta m=755.10-3 [kg],
długość l=795.10-3 [m],
![]()
![]()
Obliczenie błędu dla IS z prawa przenoszenia błędów:
![]()
Wartość ΔIS= 0,1.10-3 [kg.m2]
wyznaczenie momentu bezwładności pierścienia.
Dane:
waga pierścienia m=1439 [g]=1,44 [kg], Δm=0,1 [g]=0,1.10-3 [kg]
promień wewnętrzny obręczy Rw=12,5 [cm]=0,125 [m], promień zewnętrzny obręczy
Rz=14 [cm]=0,14 [m],odległość od środka ciężkości do osi obrotu a=12,7 [cm]=0,127 [m], Δa=0,1 [mm]=0,1.10-3 [m]
przyspieszenie ziemskie g=9,81 [m/s2]
Lp. |
Czas t [s] |
t/40 |
1 |
40,25 |
1,01 |
2 |
40,62 |
1,02 |
3 |
40,51 |
1,01 |
4 |
40,94 |
1,02 |
5 |
40,62 |
1,02 |
6 |
40,40 |
1,01 |
7 |
40,50 |
1,01 |
8 |
40,56 |
1,01 |
9 |
40,37 |
1,01 |
10 |
40,47 |
1,01 |
![]()
Wartość średnia czasu 40 wahnięć wynosi:
![]()
Wartość czasu jednego okresu wynosi:
Błąd ΔT wynosi:
ΔT= 1,46.10-3 [s]
Moment bezwładności wynosi:
I0= 46,65.10-3 [kg.m2]
Z prawa przenoszenia błędów wyznaczamy błąd momentu bezwładności:
![]()
= 0,14.10-3 [kg.m2]
Procentowy błąd przy obliczaniu momentu bezwładności:
δ=0,3[%].
Wykorzystując tw. Steinera :
![]()
wyznaczamy moment bezwładności względem środka ciężkości:
![]()
gdzie:
I0= 46,65.10-3 [kg.m2]
m=1,44 [kg],
a=127.10-3 [m],
![]()
Obliczenie błędu dla IS z prawa przenoszenia błędów:
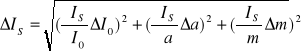
gdzie:
ΔI0= 0,14.10-3 [kg.m2]
Wartość ΔIS= 0,15.10-3 [kg.m2]
![]()
Procentowy błąd momentu bezwładności:
δ=0,63 [%].
Obliczenie wartości momentu bezwładności IS na podstawie zmierzonych wartości masy i wymiarów geometrycznych:
waga pręta m=1,44 [kg],
Rw=0,125 [m],
Rz=0,14 [m],
![]()
![]()
Obliczenie błędu dla IS z prawa przenoszenia błędów:
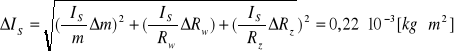
badanie funkcji rozkładu błędu pomiaru czasu.
-dla pręta:
Zmienna t została podzielona na równe przedziały o szerokości ε=0,04.
Tabela pomiarowa:
Lp. |
Przedziały |
|||||||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
XI |
XII |
XIII |
XIV |
1 |
2,31 |
2,35 |
2,38 |
2,41 |
2,47 |
2,50 |
2,54 |
2,59 |
2,63 |
2,65 |
2,70 |
2,75 |
2,78 |
2,80 |
2 |
2,31 |
2,34 |
2,38 |
2,40 |
2,47 |
2,50 |
2,54 |
2,59 |
2,63 |
|
2,70 |
2,75 |
2,78 |
2,80 |
3 |
2,30 |
|
2,37 |
2,40 |
2,45 |
2,50 |
2,54 |
2,58 |
2,63 |
|
2,69 |
2,75 |
2,78 |
2,80 |
4 |
2,30 |
|
2,37 |
|
2,45 |
2,50 |
2,53 |
2,58 |
2,63 |
|
2,69 |
2,75 |
2,78 |
2,80 |
5 |
2,28 |
|
|
|
|
2,50 |
2,53 |
2,57 |
2,63 |
|
2,69 |
2,72 |
2,78 |
2,80 |
6 |
|
|
|
|
|
2,50 |
2,53 |
2,57 |
2,63 |
|
2,68 |
2,72 |
2,78 |
2,80 |
7 |
|
|
|
|
|
2,50 |
2,53 |
2,56 |
2,62 |
|
2,68 |
2,72 |
2,78 |
|
8 |
|
|
|
|
|
2,48 |
2,53 |
2,56 |
2,62 |
|
2,68 |
|
2,78 |
|
9 |
|
|
|
|
|
2,47 |
2,53 |
2,56 |
2,62 |
|
2,68 |
|
2,78 |
|
10 |
|
|
|
|
|
2,47 |
2,53 |
2,56 |
2,62 |
|
|
|
2,78 |
|
11 |
|
|
|
|
|
|
|
2,56 |
2,60 |
|
|
|
2,77 |
|
12 |
|
|
|
|
|
|
|
2,56 |
2,60 |
|
|
|
2,77 |
|
13 |
|
|
|
|
|
|
|
2,56 |
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
2,56 |
|
|
|
|
|
|
15 |
|
|
|
|
|
|
|
2,56 |
|
|
|
|
|
|
16 |
|
|
|
|
|
|
|
2,56 |
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
2,56 |
|
|
|
|
|
|
Z tabeli można łatwo odczytać ile pomiarów ni trafiło do każdego z przedziałów.
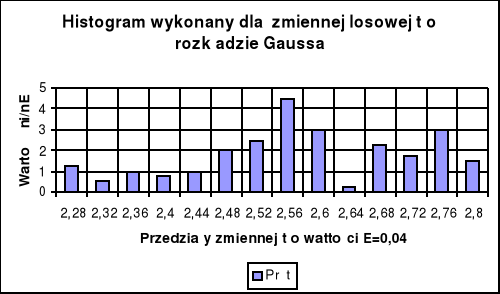
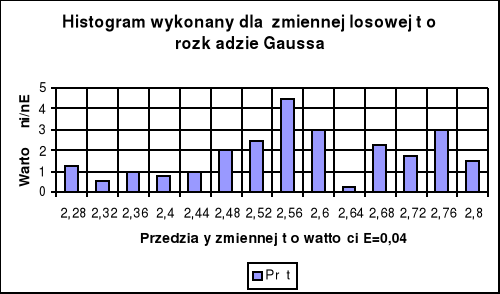
Histogram rozkładu błędów :
Wartość średnia czasu wynosi:
![]()
odchylenie standardowe pojedynczego pomiaru wynosi:
δ= 0,14 [s]
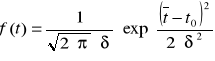
Wartość średnia czasu odpowiada ósmemu przedziałowi. Liczba pomiarów w przedziale o szerokości ±Δt wokół wartości średniej wynosi 40. Natomiast liczba pomiarów wychodzących poza przedział ±3Δt wynosi 39.
gdzie:
δ= 0,14 [s]
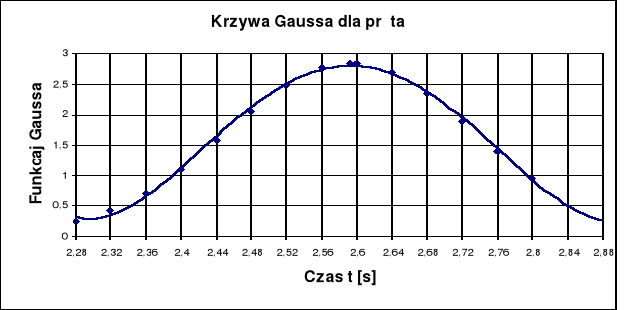
![]()
t0 - przedziały zmiennej t o wartości 0,04 [s], dla pręta.
-dla pierścienia:
Zmienna t została podzielona na równe przedziały o szerokości ε=0,04.
Tabela pomiarowa:
Lp. |
Przedziały |
|||||||||||||
|
I |
II |
III |
IV |
V |
VI |
VII |
VIII |
IX |
X |
XI |
XII |
XIII |
XIV |
1 |
1,35 |
|
1,41 |
1,45 |
1,49 |
1,53 |
1,57 |
1,61 |
1,65 |
1,69 |
1,74 |
1,78 |
1,82 |
1,88 |
2 |
1,35 |
|
1,41 |
1,47 |
1,50 |
1,53 |
1,58 |
1,62 |
1,65 |
1,69 |
1,74 |
1,78 |
1,83 |
1,88 |
3 |
1,35 |
|
1,41 |
1,47 |
1,52 |
1,53 |
1,58 |
1,62 |
1,65 |
1,69 |
1,75 |
1,78 |
1,84 |
|
4 |
|
|
1,42 |
1,47 |
1,52 |
1,54 |
1,58 |
1,62 |
1,65 |
1,69 |
1,75 |
1,79 |
1,84 |
|
5 |
|
|
1,42 |
1,47 |
1,52 |
1,54 |
1,58 |
1,62 |
1,65 |
1,69 |
|
1,80 |
1,84 |
|
6 |
|
|
1,43 |
|
|
1,56 |
1,59 |
1,62 |
1,65 |
1,69 |
|
1,80 |
1,84 |
|
7 |
|
|
1,43 |
|
|
1,56 |
1,59 |
1,62 |
1,65 |
1,70 |
|
1,80 |
1,84 |
|
8 |
|
|
1,43 |
|
|
1,56 |
1,60 |
1,63 |
1,66 |
1,71 |
|
1,80 |
|
|
9 |
|
|
1,43 |
|
|
1,56 |
1,60 |
1,63 |
1,68 |
1,72 |
|
|
|
|
10 |
|
|
|
|
|
1,56 |
1,60 |
1,63 |
1,68 |
1,72 |
|
|
|
|
11 |
|
|
|
|
|
1,56 |
1,60 |
1,63 |
|
1,72 |
|
|
|
|
12 |
|
|
|
|
|
1,56 |
|
1,64 |
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
1,64 |
|
|
|
|
|
|
Z tabeli można łatwo odczytać ile pomiarów ni trafiło do każdego z przedziałów.
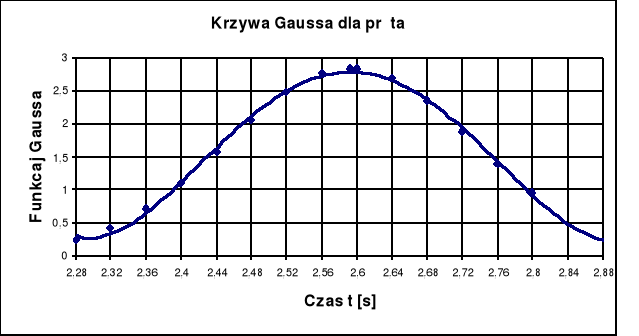
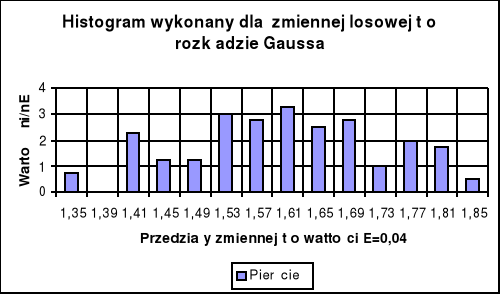
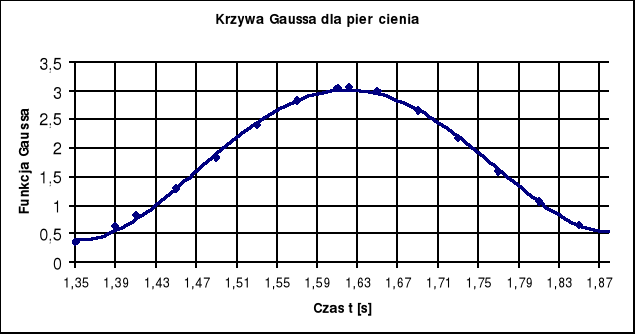
Histogram rozkładu błędów :
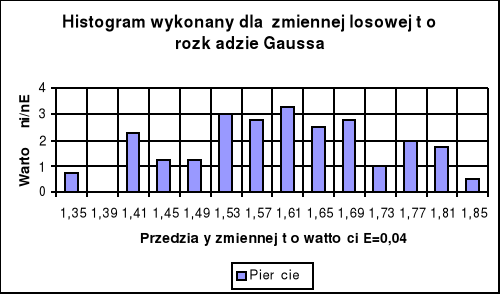
Wartość średnia czasu wynosi:
![]()
odchylenie standardowe pojedynczego pomiaru wynosi:
δ= 0,13 [s]
Wartość średnia czasu odpowiada ósmemu przedziałowi. Liczba pomiarów w przedziale o szerokości ±Δt wokół wartości średniej wynosi 34. Natomiast liczba pomiarów wychodzących poza przedział ±3Δt wynosi 39.
![]()
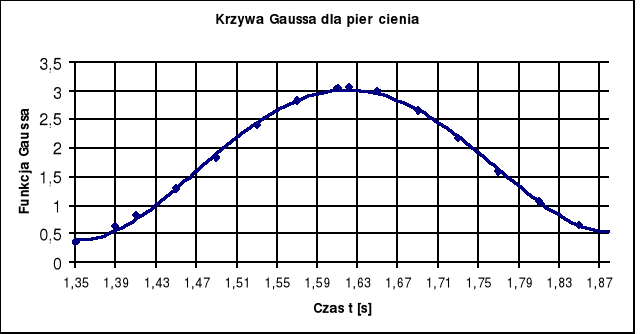
Krzywa Gaussa obliczona przy pomocy wzoru jak dla pręta, gdzie:
δ= 0,13 [s]
t0 - przedziały zmiennej t o wartości 0,04 [s], dla pierścienia.
4. Wnioski
Wartości momentów bezwładności uzyskano za pomocą dwóch metod:
1)pomiaru okresu drgań wahadła fizycznego, a następnie obliczenia momentu z odpowiedniego wzoru
2)zmierzenia masy i wymiarów, a następnie obliczenia momentu ze wzoru.
Otrzymane wyniki są porównywalne dla pomiarów otrzymanych na oba sposoby:
dla pręta:
1)![]()
2) ![]()
)
dla pierścienia:
1) ![]()
2) ![]()
jednak pomiary wykonywane pierwszą metodą są obarczone dodatkowo błędem systematycznym wynikającym z tłumienia drgań.
1
9
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
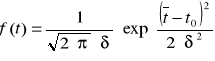
![]()
![]()
Wyszukiwarka
Podobne podstrony:
Califone 3410 Cassette
3410
200401 3410
3410
3410
3410
3410
3410
3410
3410 3411
Califone 3410 Cassette(1)
3410(1)
Valerie Parv Lightning s Lady [HR 3125, MB 3410] (v0 9) (docx) 2
więcej podobnych podstron