Zadanie 1

• Dobór miar - do porównania zbiorowości używamy parametrów pozycyjnych. Przedziały klasowe są otwarte. W ostatnim (dla zbiorowości studentów socjologii) mieści się 15% jednostek zbiorowości, co wyklucza umowne domknięcie przedziału a tym samym zastosowanie parametrów klasycznych.

Tabela 1

Liczba filmów obejrzanych w kinie w ciągu minionego roku	ns	ns ^cum	np.	np. ^cum
	socjologia		psychologia
Poniżej 2	3	3	2	2
2-4	8	11	21	23
4-6	29	40	23	49
6-8	24	64	33	79
8-10	21	85	16	95
Powyżej 10	15	100	5	100

• Porównanie parametrów:

1. dominanty,

2. mediany,

3. kwartyli - Q1 i Q3,

4. rozstępu kwartylowego,

5. odchylenia ćwiartkowego,

6. pozycyjnego współczynnika zmienności,

7. pozycyjnego współczynnika asymetrii

obliczonych wg wzorów:

Dominanta
Mediana

Kwartyl pierwszy
Kwartyl trzeci

Rozstęp kwartylowy
Odchylenie ćwiartkowe

Pozycyjny współczynnik zmienności

Współczynnik asymetrii oparty o kwartyle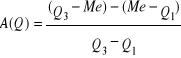

przedstawia się następująco:

Tabela 2

Miary	socjologia	psychologia
dominanta	5,61	6,74
mediana	6,83	6,24
kwartyl pierwszy	4,97	4,17
kwartyl trzeci	9,05	7,76
rozstęp kwartylowy	4,08	3,59
odchylenie ćwiartkowe	2,04	1,795
pozycyjny współczynnik zmienności	29,87%	28,77%
pozycyjny współczynnik asymetrii	0,088	-0,153

• Interpretacja (wyniki zaokrąglono do liczb całkowitych):

• dominanta - najwięcej studentów socjologii obejrzało w ubiegłym roku w kinie 6 filmów, najwięcej studentów psychologii - 7 filmów,

• mediana - połowa studentów socjologii UG obejrzała w ubiegłym roku mniej niż 7 filmów, druga połowa zaś - 7 filmów i więcej; 50% studentów psychologii obejrzało w ubiegłym roku 6 filmów i mniej, pozostałe 50% - więcej niż 6 filmów,

• kwartyl pierwszy - 25% studentów socjologii obejrzało mniej niż 5 filmów, pozostałe 75% - 5 filmów i więcej, w przypadku studentów psychologii - 1/4 obejrzała 4 filmy i mniej, zaś pozostałe 3/4 - więcej niż 4 filmy,

• kwartyl trzeci - 3/4 studentów socjologii obejrzało w ubiegłym roku w kinie co najwyżej 9 filmów, pozostała 1/4 obejrzała więcej niż 9 filmów; 75% studentów psychologii obejrzało w ubiegłym roku mniej niż 8 filmów, pozostałe 75% - 8 filmów lub więcej.

• rozstęp kwartylowy - w przypadku obu zbiorowości obszar środkowych 50% jednostek zbiorowości wynosi w przybliżeniu 4 (filmy),

• odchylenie ćwiartkowe - przeciętne zróżnicowanie ilości obejrzanych filmów wokół wartości środkowej wynosi - dla studentów socjologii około 2 filmów, dla studentów psychologii - 1,8 (jest to połowa obszaru zmienności środkowych 50% jednostek zbiorowości),

• pozycyjny współczynnik zmienności - odchylenie ćwiartkowe w przypadku studentów socjologii stanowi 29,87% środkowej wartości liczby filmów obejrzanych podczas ubiegłego roku w kinie. Dla studentów psychologii wartość ta jest równa 28,77%,

• pozycyjny współczynnik asymetrii - rozkład ilości filmów obejrzanych w kinie podczas ubiegłego roku przez studentów socjologii charakteryzuje bardzo słaba asymetria dodatnia, która wskazuje na to, że nieznacznie więcej studentów obejrzało mniej filmów niż 7 ( D<Me). W przypadku studentów psychologii rozkład charakteryzuje niewielka asymetria ujemna - więcej studentów obejrzało więcej filmów niż wynosi wartość mediany (6) - D>Me.

Zadanie 2

Rozkład liczby studentek wg ponoszonych przez nie wydatków na książki jest symetryczny, ma domknięte przedziały klasowe, charakteryzuje się tendencją centralną - zatem dla porównania zbiorowości studentek i studentów można używać parametrów klasycznych.

Informacja nt zbiorowości studentów jest ograniczona, dlatego porównywać będziemy jedynie:

• średnie arytmetyczne,

• odchylenia standardowe,

• współczynniki zmienności,

• typowe obszary zmienności,

• dominanty,

• mieszane współczynniki asymetrii

odpowiednio wg wzorów:

średnia arytmetyczna: , gdzie będzie oznaczało środki kolejnych przedziałów klasowych, obliczanych na podstawie wzoru: ,

wariancja: ,

odchylenie standardowe: ,

współczynnik zmienności
,

typowy obszar zmienności

dominanta - wg wzoru z zad.1,

mieszany współczynnik asymetrii

Obliczenia pomocnicze znajdują się w tabeli 3:

Tabela 3

<xi0 ; xi1)	ni	xi0	xi0*ni	(xi0-xśr)^2*ni	wsk (xi0ni)	wsk cum (xi0ni)	wsk(ni)	wsk cum (ni)	"pole b"
0-25	8	12,5	100	17484,5	1,69%	1,69%	8%	8%	6,75
25-50	21	37,5	787,5	9934,3125	13,29%	14,98%	21%	29%	175,00
50-75	51	62,5	3187,5	538,6875	53,80%	68,78%	51%	80%	2135,76
75-100	16	87,5	1400	12769	23,63%	92,41%	16%	96%	1289,45
100-125	4	112,5	450	11342,25	7,59%	100,00%	4%	100%	384,81
SUMA	100	x	5925	52068,75	100,00%	X	100%	X	3991,77

Tabela 4 - Porównanie miar:

Miary	studenci	studentki
średnia arytmetyczna	55	59,25
odchylenie standardowe	16,5	22,82
współczynnik zmienności	30%	38,51%
dominanta	50	61,54
typowy obszar zmienności	[38,5; 71,5]	[36,43; 82,07]
mieszany współczynnik asymetrii	0,303	-0,1

Interpretacja:

Studenci wydawali średnio na książki 55 zł, studentki zaś - 59,25 zł.

Przeciętne odchylenie wielkości wydatków na książki od średniego poziomu wydatków na ten cel w przypadku studentów wynosiło 16,5 zł, w przypadku studentek - 22,82 zł.

Przeciętne odchylenia wielkości wydatków na książki stanowi 30% średniego poziomu wydatków studentów na ten cel - i 38,51% średniego poziomu wydatków studentek.

Dwie powyższe wartości wskazują, że wydatki studentek na zakup książek cechuje większe rozproszenie.

Najwięcej studentów wydało na zakup książek 50 zł, najwięcej studentek - 61,54 zł.

Typowe miesięczne wydatki studentów na zakup książek mieszczą się w przedziale [38,5; 71,5], studentek zaś - w przedziale [36,43; 82,07].

Rozkład wydatków studentów cechuje słaba asymetria dodatnia, co oznacza, że więcej studentów wydało na zakup książek mniej niż wskazywałaby na to wartość średnia (czyli mniej niż 55 zł); rozkład wydatków studentek jest ujemnie asymetryczny, co oznacza, że więcej studentek wydatkowało na zakup książek więcej niż 58,25 zł miesięcznie.

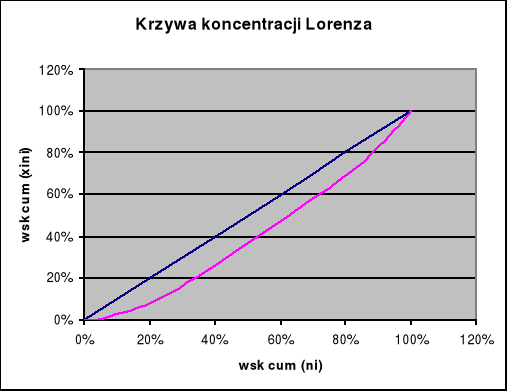
Określenie siły koncentracji wydatków na książki poniesionych przez studentki WA AM:

• za pomocą współczynnika koncentracji Pearsona K:

gdzie

"pole b" zostało policzone w tabeli 3.

K=0,2016 - oznacza to, iż koncentracja wydatków studentek na książki jest umiarkowana (K zawiera się w przedziale [0, 1])

Krzywa koncentracji Lorenza znajdująca się blisko linii równomiernego podziału potwierdza otrzymany numerycznie wynik:

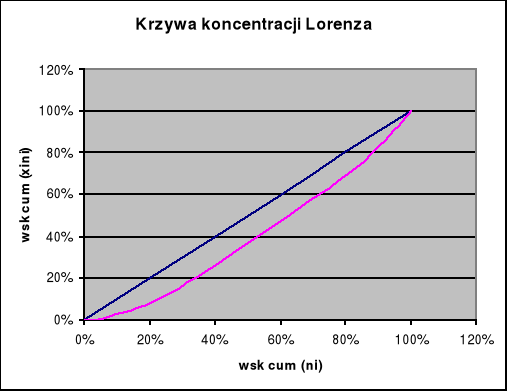
Zadanie 3

1. aby zadana funkcja była funkcją gęstości, całka po całej powierzchni musi być równa 1. Z tego otrzymujemy C=-12.

2. dystrybuanta ma postać

0 dla x<0

F(x)= 4x³-3x⁴ dla 0≤x≤1

1 dla x>1

3. wartość oczekiwana obliczona zgodnie ze wzorem
   wynosi 0,6.

Odchylenie standardowe, jako pierwiastek z wariancji (wariancja to drugi moment centralny - wg wzoru na moment centralny rzędu k:
) - jest równe 0,2.

4) P(0,5 ≤ X ≤ 1,5) = F (1,5) - F(0,5) = 0,6875.

Zadanie 4

X ~N(12, 2)

1. 
   = 0,9773

a=16

2. P( | X-12 | <2) = P( -2 < X-12 < 2) =
   
   = F(1)-F(-1) =

(korzystamy z tablic dystrybuanty standaryzowanego rozkładu normalnego)

Zadanie 5

X ~N(40, 5)

Zadanie 6

Korzystamy z rozkładu różnicy średnich, wg wzoru:

Dla: X₁ ~N(m₁, σ₁) X₂ ~N(m₂, σ₂)

~

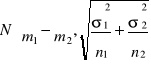
Żony: X₁ ~N(69, 9), n₁=10

Mężowie: X₂ ~N(82, 8), n₂=13

~
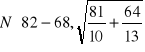
~ N(14, 3,61)

P(
≥5) =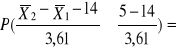
P(Z≥-2,49)=F(2,49)=0,993613

(korzystamy z wartości dystrybuanty standaryzowanego rozkładu normalnego)

Zadanie 7

Do weryfikacji hipotezy wykorzystujemy test niezależności χ², który służy do wnioskowania o związku między zmiennymi (zarówno jakościowymi, jak i ilościowymi).

1. Formułujemy hipotezę zerową, która zakłada, że wykształcenie i źródło informacji o produkcie są cechami niezależnymi. Hipoteza alternatywna stwierdza, że źródło informacji ma związek z wykształceniem nabywców:

H₀:

H₁:

Warunkiem niezależności zmiennych losowych wyrażonych w skali nominalnej (jakościowych) X, Y jest to, aby dla wszystkich par (x_i,y_j) zaobserwowanych wartości tych zmiennych zachodziła równość:
, co można zapisać:
,

gdzie:
- łączna funkcja prawdopodobieństwa zmiennej X, Y;

- brzegowa funkcja prawdopodobieństwa zmiennej X;

- brzegowa funkcja prawdopodobieństwa zmiennej Y.

2. Dla każdego pola tablicy niezależności (patrz tabela 5a):

Tabela 5a:

Wykształcenie	Źródło informacji			Razem
		Reklamy w TV	Reklamy w pismach		Inne
Wyższe	8	70	12	90
Średnie	70	140	30	240
Podstawowe i zawodowe	52	10	8	70
Razem	130	220	50	420

Obliczamy liczebności teoretyczne
- czyli takie liczby jednostek, których należałoby oczekiwać, gdyby cechy były niezależne - wg wzoru:
.

3. Obliczamy statystykę χ2 - wg wzoru: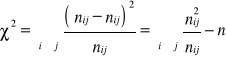
   {liczba stopni swobody: ν = (k - 1)·(l - 1)}

Obliczenia pomocnicze zapisujemy w tabeli roboczej - tabela 5b:

Tabela 5b:

8	29,25	451,5625	15,4380342
70	49,5	420,25	8,4898990
12	11,25	0,5625	0,0500000
70	78	64	0,8205128
140	132	64	0,4848485
30	30	0	0
52	22,75	855,5625	37,6071429
10	38,5	812,25	21,0974026
8	8,75	0,5625	0,0642857
SUMA	x	x	84,0521257

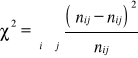
= 84,052

4. Z tablic rozkładu chi-kwadrat odczytujemy wartość krytyczną dla poziomu istotności α=0,05 i liczby stopni swobody (3-1)·(3-1)=4:
   

5. Wartość statystyki obliczona z próby jest większa od wartości krytycznej odczytanej z tabeli:
   (należy do obszaru krytycznego).

Na poziomie istotności α = 0,05 odrzucamy hipotezę zerową mówiącą o niezależności źródła informacji od poziomu wykształcenia. Badane cechy statystycznie istotnie zależą od siebie.

Zadanie 8

Obliczenia pomocnicze do zadania znajdują się w tabeli 6:

Tabela 6

i
1	0	1000	-3	490	-1470	9	240100	0	0	952,5	2256,25
2	1	900	-2	390	-780	4	152100	900	1	805	9025
3	2	500	-1	-10	10	1	100	1000	4	657,5	24806,25
4	3	500	0	-10	0	0	100	1500	9	510	100
5	4	270	1	-240	-240	1	57600	1080	16	362,5	8556,25
6	5	300	2	-210	-420	4	44100	1500	25	215	7225
7	6	100	3	-410	-1230	9	168100	600	36	67,5	1056,25
suma	21	3570	0	0	-4130	28	662200	6580	91	x	53025

1. Współczynnik korelacji Pearsona, obliczamy wg wzoru:

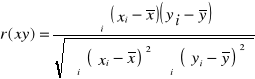
wynosi - 0.959.

Oznacza to, że pomiędzy odległością od centrum miasta (w km) a ceną 1 m² działki istnieje silny związek korelacyjny ujemny. Wraz ze zwiększaniem się odległości od centrum, cena 1 m² działki maleje.

2) liniowa funkcja regresji
,

parametry szacujemy MNK, wg wzoru:

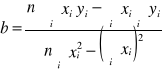
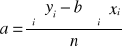
b = -147,5

a = 952,5

Wraz ze wzrostem odległości działki od centrum o 1m, cena 1m² działki spada przeciętnie o 147,50 zł.

3) Badamy dopasowanie modelu do danych empirycznych:

• wariancja resztowa: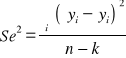
  =10605

• odchylenie standardowe składnika resztowego: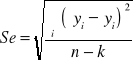
  =102,98

(k jest liczbą szacowanych parametrów funkcji regresji)

• współczynnik zmienności przypadkowej:
  

Ve=20,192%

Interpretacja: Faktycznie zaobserwowane ceny 1m² działki różnią się od oszacowanych za pomocą liniowej funkcji regresji średnio o 102,98 zł, co stanowi 20,192% przeciętnego poziomu ceny 1m² działki.

• współczynnik indeterminacji (zbieżności):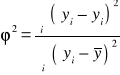
  = 0,08

• współczynnik determinacji:
  = 0,92

Interpretacja: 92% zmienności ceny 1m² działki jest wywołane zmianami odległości działki od centrum, natomiast pozostałe 8% zmienności jest skutkiem działania innych czynników.

WNIOSEK: Model jest dobrze dopasowany do danych empirycznych.

4. Sprawdzamy, czy wpływ zmiennej niezależnej jest statystycznie istotny.

Wykorzystujemy w tym celu test istotności współczynnika regresji liniowej w modelu

• Hipoteza zerowa zakłada brak wpływu odległości od centrum na cenę, natomiast hipoteza alternatywna stwierdza, że wpływ zmiennej niezależnej na zależną jest statystycznie istotny:

H₀: β = 0

H₁: β ≠ 0

• Obliczamy statystykę t-Studenta wg wzoru:

(liczba stopni swobody: ν = n - 2)

t = - 7,5791

• Z tablic rozkładu t-Studenta odczytujemy wartość krytyczną dla α=0,05 i liczby stopni swobody równej 5: t_α = t(0,05; 5) = 2,571

• Porównując statystykę obliczoną z próby z wartością krytyczną stwierdzamy, że zachodzi relacja │t│≥ t_α, zatem wartość statystyki znajduje się w obszarze krytycznym.

Na poziomie istotności α=0,05 odrzucamy hipotezę zerową na rzecz hipotezy alternatywnej. Wpływ odległości działki od centrum na cenę 1m² działki jest statystycznie istotny.

5. Sprawdzając założenie o liniowości funkcji regresji weryfikujemy hipotezę:

H₀: E(Y/X=x)= α +βx (regresja w populacji generalnej jest liniowa)

H₁: E(Y/X=x)≠ α +βx (regresja w populacji generalnej nie jest liniowa)

(sprawdzamy losowość reszt - czyli przypadkowy charakter odchyleń od funkcji regresji)

Weryfikacja założenia jest dokonywana za pomocą testu serii:

• obliczamy różnice
  i przyporządkowujemy im odpowiedni symbol:

a dla
>0, b dla
<0 (reszty równe 0 usuwa się z próby)

• w uporządkowanym wg rosnących wartości
  ciągu wyznaczamy liczbę serii k (tabela 7):

Tabela 7

			-	symbol
0	1000	952,5	+	a
1	900	805	+	a
2	500	657,5	-	b
3	500	510	-	b
4	270	362,5	-	b
5	300	215	+	a
6	100	67,5	+	a

Ustawienie symboli w ostatniej kolumnie tablicy 7 wskazuje, że w szeregu wystąpiło k=3 serii.

• wartość krytyczna dla α=0,05 oraz n₁ =4 (liczba znaków a) oraz n₂ =3 (liczba znaków b) odczytana z tablic rozkładu serii wynosi kα=k(0,05; 4; 3)=2

• Zaobserwowana liczba serii jest większa od wartości krytycznej k > kα, co przy lewostronnym obszarze krytycznym oznacza, że statystyka znalazła się poza tym obszarem.

Na poziomie istotności α=0,05 nie ma podstaw do odrzucenia hipotezy zerowej mówiącej o tym, że regresja cen 1m² działek względem odległości działek od centrum była liniowa w całej populacji.

Zadanie 9

Obliczenia pomocnicze do zadania znajdują się w tabeli 8.

Tabela 8:

20-30	4	2	25	100	50	2061,16	915,92
30-40	16	20	35	560	700	2580,64	2599,2
40-50	38	46	45	1710	2070	277,02	90,16
50-60	34	26	55	1870	1430	1811,86	1922,96
60-70	7	6	65	455	390	2095,03	2075,76
70-80	1	0	75	75	0	745,29	0
SUMA	100	100	x	4770	4640	9571	7604

• obliczamy średnie ayrtmetyczne wg wzoru:

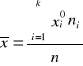
= 47,7
= 46,4

• oraz wariancje wg wzoru:

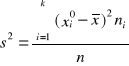
= 95,71
=76,04

1. Weryfikacja hipotezy o równości wariancji w obu populacjach:

H₀:

H₁ :

Do weryfikacji hipotezy wykorzystujemy statystykę postaci:

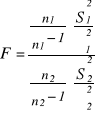
, która ma rozkład Fishera-Snedecora z ν₁ = n₁ -1 i ν₂ = n₂ -1 stopniami swobody.

Ponieważ n₁ = n₂ = 100, statystyka przyjmuje postać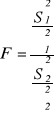
.

Zakładając prawdziwość hipotezy zerowej σ₁²= σ₂² , statystyka jest równa
.

Na podstawie powyższego wzoru otrzymujemy F=1,2587

Obliczoną wartość porównujemy z wartością krytyczną, która dla poziomu istotności α=0,05 i liczby stopni swobody ν₁= ν₂=99 wynosi 1,39.

F<
, zatem statystyka F nie wpada do obszaru krytycznego testu.

Na poziomie istotności α=0,05 nie ma podstaw do odrzucenia hipotezy zerowej o równości wariancji w obu populacjach.

2. Weryfikacja hipotezy o jednakowych średnich wieku w obu populacjach:

H₀: m₁ = m₂

H₁ : m₁ ≠ m₂

(dwie próby niezależne; nieznane σ₁, σ_2; σ₁² = σ₂²; próby duże).

Do weryfikacji hipotezy przy w/wym założeniach używamy statystyki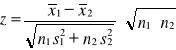

z=0,992

Otrzymaną wartość porównujemy z wartością krytyczną, która dla standaryzowanego rozkładu normalnego, na poziomie istotności α=0,05 wynosi z_α=1,96.

z< z_α, zatem

na poziomie istotności α=0,05 nie ma podstaw do odrzucenia hipotezy zerowej mówiącej o tym, że średni wiek posłów I i II kadencji nie różni się istotnie od siebie.

mgr Sabina Nowak - zadania ze statystyki (studia dzienne)

- rozwiązania -

1

mgr Sabina Nowak - zadania ze statystyki - (studia dzienne)

- rozwiązania -

8

---