WSTĘP TEORETYCZNY

Badanie rezonansu w obwodach elektrycznych

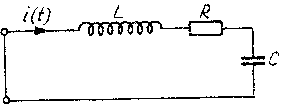
Zjawisko rezonansu związane jest z wymuszonymi drganiami układów drgających. Pojęcie wymuszenia drgań oznacza, że do układu ciał drgających zostaje cały czas doprowadzana energia w postaci siły harmonicznej, która nie pozwala na stłumienie drgań. Częstotliwość dostarczania porcji energii przez tę siłę może być tak dobrana, że układ będzie miał duże wychylenia bardzo małym kosztem dostarczanej energii. Szczególnym przypadkiem układu rezonansowego jest obwód RLC widoczny na rysunku obok:

Załóżmy, że w pewnym momencie następuje rozładowanie kondensatora C z ładunku q a prąd płynący przez cewkę oraz przez rezystor jest równy 0. Wraz z upływem w czasie ładunku kondensatora
zmniejsza się zgromadzona energia elektryczna na kondensatorze. Energia zgromadzona w układzie nigdzie nie ginie lecz jest gromadzona na cewce w postaci pola elektromagnetycznego. Część energii jest wytracana na rezystorze w postaci ciepła Joule'a. Jeden pełny cykl następuje, gdy wektor pola elektrycznego ma ten sam zwrot. Zmianę ładunku zgromadzonego na kondensatorze określa poniższe równanie różniczkowe:

Wprowadzając oznaczenia:
oznaczające tłumienie oraz
oznaczające częstotliwość drgania układu wzór upraszcza się do postaci:
.

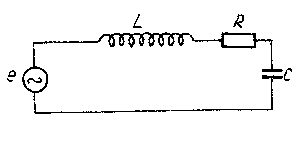
Jeżeli rozpatrywany układ zmodyfikujemy dołączając siłę elektromotoryczną, która jest harmoniczna, wówczas równanie różniczkowe opisujące zmianę zgromadzonego ładunku na kondensatorze skomplikuje się do postaci:

Rozwiązując powyższe równanie różniczkowe możemy wyznaczyć funkcję według której zmienia się ładunek na kondensatorze:

,

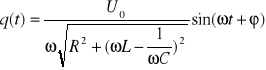
a napięcia chwilowe na kondensatorze i cewce będą odpowiednio równe:

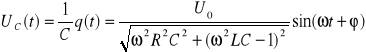
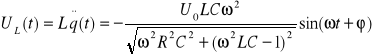
Dla R=0 i
wynika, że napięcie na kondensatorze jest równe co do modułu napięciu na cewce lecz przeciwne co do znaku.

Z zależności tych wynika, że dla układów bezstratnych (R=0) istnieje taka wartość częstości siły wymuszającej e(t) dla której wartości napięć U_C i U_L mogą być bardzo duże. Zjawisko to nazywa się rezonansem szeregowym w obwodzie RLC.

Częstość dla której zachodzi owo zjawisko nosi nazwę częstości rezonansowej i jest ona określana wzorem:

Dla układów ze stratnością wzór na częstotliwość rezonansową przekształca się do postaci:

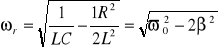
Jedną z najważniejszych wielkości charakteryzujących obwód rezonansowy jest dobroć układu. Definiuje się ją jako stosunek napięcia na kondensatorze do amplitudy siły elektromotorycznej zasilającej harmonicznie układ. Dla naszego układu rezonansowego dobroć określa wzór:

,

gdzie f_r to częstotliwość rezonansowa.

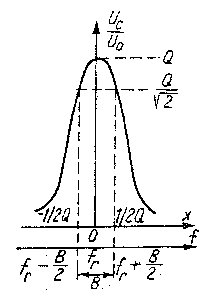
Dla układu RLC można wyznaczyć pasmo przenoszenia częstotliwości, które określa krzywa rezonansowa widoczna na rysunku obok. Pasmo częstotliwości obwodu jest to przedział częstotliwości dla których stosunek dobroci układu dla częstotliwości granicznych do dobroci układu dla częstotliwości rezonansowej wynosi
.

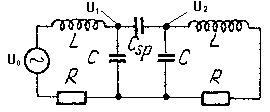
Pasmo przenoszenia B układu RLC można poszerzać stosując sprzężenia 2 lub więcej układów RLC poprzez pojemność lub indukcyjność bądź rezystancję. Skupmy się na sprzężeniu pojemnościowym bowiem to jest rzeczą tego ćwiczenia laboratoryjnego. Przykładem 2 obwodów RLC sprzężonych pojemnościowo może być układ z rysunku obok:

Analizując ten układ będą nas interesowały dwa stosunki napięć:
oraz
. Pierwszy z nich powinien być zbieżny z rozwiązaniem podanym wyżej dla układu nie sprzężonego a drugi powinien dla
być równy 0 i przedstawiać szukaną charakterystykę częstotliwościową obwodu rezonansowego sprzężonego dla
.

Rozwiązując ten układ metodą oczkową korzystając z II prawa Kirchoffa uzyskamy układy równań napięć i prądów występujących w każdym oczku tego obwodu. Wszystkie te zależności można zapisać w postaci macierzowej a z niej, korzystając ze wzorów Cramera można uzyskać nam stosunek napięć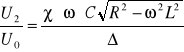
, gdzie

Dla układów o bardzo małych stratach (R małe, Q>>1) stosunek napięć
osiągnie maksimum, gdy
osiągnie minimum, w przypadku skrajnym gdy R=0 i
=0 dla
i
, przy założeniu że
. Wprowadźmy częstość średnią
oraz częstość względną zdefiniowaną jako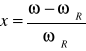
i dobroć
. Wtedy można rozpatrzyć następujące przypadki:

Jeżeli
to mamy jeden punkt ekstremalny dla x=0, wtedy:

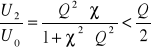
- jest to tzw. sprzężenie podkrytyczne.

Jeżeli
to mamy wtedy sprzężenie krytyczne, a wtedy również mamy jeden punkt ekstremalny i
dla x=0

Jeżeli
to mamy trzy punkty ekstremalne dla
oraz: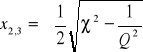
- ten stan nazywamy sprzężeniem nadkrytycznym.

Powyższe przypadki dobrze obrazuje rysunek:

Wyniki pomiarów:

		C1=82pF	C2=130pF	C3=240pF
f [Hz]	U0 [V]	U1 [V]	U2 [V]	U3 [V]
13000	1,666	0,125	0,250	0,693
13100	1,612	0,158	0,315	0,908
13200	1,590	0,201	0,404	1,220
13300	2,200	0,260	0,528	1,690
13400	2,457	0,345	0,713	2,420
13500	2,766	0,468	0,989	3,468
13600	3,175	0,656	1,420	4,460
13700	3,690	0,952	2,110	4,465
13800	4,370	1,436	3,110	4,303
13900	5,270	2,190	4,060	4,026
14000	6,444	3,190	4,375	3,950
14100	7,510	3,748	4,349	4,120
14200	7,900	3,888	4,379	4,457
14300	7,282	3,772	4,313	4,635
14400	6,112	3,222	3,733	4,150
14500	5,015	2,313	2,731	3,145
14600	4,172	1,550	1,882	2,258
14700	3,501	1,053	1,315	1,628
14800	3,002	0,739	0,948	1,218
14900	2,605	0,538	0,708	0,937
15000	2,271	0,407	0,546	0,748

U_x [V] - Zmierzone napięcia,

C [pF] - Zdefiniowane pojemności,

U= 10 [V] ­­- Przyłożone napięcie

L= 30,6e-3 [H]

C= 3,9e-9 [F]

R= 40 [Ω]

∆L=∆C=∆R= ±5%

OPRACOWANIE WYNIKÓW POMIARÓW

I. Wykres zależności U_c(x).

x	U0 [V]
-0,0845	1,666
-0,0775	1,612
-0,0704	1,590
-0,0634	2,200
-0,0563	2,457
-0,0493	2,766
-0,0423	3,175
-0,0352	3,690
-0,0282	4,370
-0,0211	5,270
-0,0141	6,444
-0,0070	7,510
0	7,900
0,0070	7,282
0,0141	6,112
0,0211	5,015
0,0282	4,172
0,0352	3,501
0,0423	3,002
0,0493	2,605
0,0563	2,271

fr= 14200 Hz

X	U1 [V]	x	U2 [V]	x	U3 [V]
-0,0845	0,125	-0,0780	0,250	-0,0714	0,693
-0,0775	0,158	-0,0709	0,315	-0,0643	0,908
-0,0704	0,201	-0,0638	0,404	-0,0571	1,220
-0,0634	0,260	-0,0567	0,528	-0,0500	1,690
-0,0563	0,345	-0,0496	0,713	-0,0429	2,420
-0,0493	0,468	-0,0426	0,989	-0,0357	3,468
-0,0423	0,656	-0,0355	1,420	-0,0286	4,460
-0,0352	0,952	-0,0284	2,110	-0,0214	4,465
-0,0282	1,436	-0,0213	3,110	-0,0143	4,303
-0,0211	2,190	-0,0142	4,060	-0,0071	4,026
-0,0141	3,190	-0,0071	4,375	0	3,950
-0,0070	3,748	0	4,349	0,0071	4,120
0	3,888	0,0071	4,379	0,0143	4,457
0,0070	3,772	0,0142	4,313	0,0214	4,635
0,0141	3,222	0,0213	3,733	0,0286	4,150
0,0211	2,313	0,0284	2,731	0,0357	3,145
0,0282	1,550	0,0355	1,882	0,0429	2,258
0,0352	1,053	0,0426	1,315	0,0500	1,628
0,0423	0,739	0,0496	0,948	0,0571	1,218
0,0493	0,538	0,0567	0,708	0,0643	0,937
0,0563	0,407	0,0638	0,546	0,0714	0,748

fr₈₂= 14200 [Hz]

fr₁₃₀= 14100 [Hz]

fr₂₄₀= 1400[Hz]

II. Wyznaczenie dobroci układów.

		C1	C2	C3
UC [V]	7,9	3,89	4,38	4,05
Q	0,79	0,39	0,44	0,41

III. Wyznaczenie pasma.

		C1	C2	C3
fr [kHz]	14,20	14,20	14,10	14,00
Q	0,79	0,39	0,44	0,41
B [kHz]	17,97	36,52	32,21	34,56

WNIOSKI

Ćwiczenie polegało na badanie układu RLC z rezonansem szeregowym oraz sprzężenia 2 identycznych układów z rezonansem szeregowym RLC poprzez pojemność. Do wyznaczenia charakterystyk częstotliwościowych układów wykonywane były pomiary napięcia na kondensatorze. Należało też wyznaczyć pasmo przenoszenia oraz dobroć układów.

Analizując charakterystyki układów można stwierdzić, że filtr RLC ze sprzężeniem jest bardziej selektywny aniżeli filtr bez sprzężenia. W układnie sprzężonym, nachylenie zbocza charakterystyki częstotliwościowej jest większe niż układu bez sprzężenia. Można także odczytać jak rodzaje sprzężeń układów rezonansowych wpływają na dobroć układu. Największą dobroć ma układ ze sprzężeniem nadkrytycznym. Nieznacznie mniejszą dobroć ma układ ze sprzężeniem krytycznym. Najmniejszą dobroć ma układ ze sprzężeniem podkrytycznym. Wynika z tego że do budowy filtru pasmowego najlepszy jest układ ze sprzężeniem krytycznym. Ten układ w przeciwieństwie do układu ze sprzężeniem nadkrytycznym jednakowo dobrze przenosi sygnały o częstotliwościach znajdujących się w pasie przepuszczania.

Błędy mogły wynikać z niedokładności komponentów: ±5% dla kondensatorów i oporników oraz niepoprawnego odczytu napięcia, spowodowanego „wariacjami” woltomierza. Mimo tych utrudnień stwierdzam, że cel ćwiczenia został osiągnięty.

---