I Wstęp
Efekt fotoelektryczny zewnętrzny jest jednym ze sposobów oddziaływania fali elektromagnetycznej, a więc i światła z materią (korpuskułami). Zjawisko to polega na wybijaniu elektronów z powierzchni metalu (fotokatody) przez padającą wiązkę światła o odpowiedniej częstości. Zjawisko to miało ogromne znaczenie dla poznania praw fizyki rządzących mikroświatem i znacznie przyczyniło się do powstania na początku XIX wieku fizyki kwantowej. Zjawisko to posiadało cechy, których nie dało się wytłumaczyć na gruncie fizyki klasycznej. Wyjaśnienie tego zjawiska wymagało zrewidowania poglądów na naturę światła traktowanego wyłącznie jako falę elektromagnetyczną.
Właściwą interpretację tego zjawiska podał Einstein odrzucając czysto falowy charakter światła i przyjmując fotonową teorię zjawiska fotoelektrycznego. Teoria ta traktuje światło jako strumień cząstek zwanych fotonami, gdzie każdy foton posiada energię równą:
E = hν
gdzie: h - stała Plancka, ν- częstotliwość światła.
Przy tym założeniu efekt fotoelektryczny jest zjawiskiem zderzenia dwóch cząstek: fotonu z elektronem metalu, na który pada światło. Dla takiego zderzenia Einstein napisał zasadę zachowania energii w postaci:
h ν= W + Emax
gdzie hν jest energią fotonu padającego na fotokatodę (metal), W - praca wyjścia elektronu, w który "uderza" foton, natomiast Emax jest maksymalną energią kinetyczną jaką może uzyskać elektron po wyjściu z fotokatody.
W większości przypadków energia elektronu będzie mniejsza na skutek strat wewnątrz metalu.
Korpuskularna teoria może wytłumaczyć wszystkie cechy zjawiska fotoelektrycznego:
niezależność Emax od natężenia światła wynika z tego, że zwiększając natężenie zwiększamy tylko liczbę fotonów, a nie ich energię co zgodnie z równaniem Einsteina nie ma wpływu na energię elektronów.
istnienie częstości granicznej zjawiska (częstości poniżej której fala nie wybija elektronów) jest warunkowane tym, że foton musi mieć pewną minimalną energię, równą pracy wyjścia W.
brak opóźnienia zjawiska wybijania w czasie jest powodowany tym, że energia dostarczana jest w postaci skończonych porcji energii (fotonów).
Jeśli przekształcimy równanie Einsteina, otrzymamy zależność pomiędzy napięciem hamowania (napięciem pomiędzy katodą a anodą, które powoduje zanik przepływu fotoprądu) a częstotliwością padającej fali. Przy założeniu, że Emax = eVh otrzymujemy:
Vh = ![]()
Teoria Einsteina przewiduje zatem liniowy związek pomiędzy potencjałem hamowania a częstotliwością.
Ogólnie można stwierdzić, że zjawisko fotoelektryczne potwierdza korpuskularną naturę światła, a łącznie ze zjawiskami np.: dyfrakcji, interferencji świadczy o dualizmie korpuskularno-falowym światła.
II. Opis ćwiczenia
Schemat układu pomiarowego, oraz opis ćwiczenia dotyczącego efektu fotoelektrycznego zewnętrznego.
Przyrządy:
fotokomórka (laboratoryjny układ fotokomórka-źródło światła z regulowanym napięciem hamującym oraz z wyjściami pomiarowymi napięcia hamującego i natężenia fotoprądu)
miernik uniwersalny (elektroniczny) służący jako woltomierz
miernik uniwersalny służący jako amperomierz (analogowy wychyłowy)
monochromator
Rys.1. Schemat układu pomiarowego :
FK - fotokomórka
P - potencjometr
B - bateria
U - napięcie mierzone woltomierzem V
I - natężenie prądu mierzone amperomierzem A
Przebieg ćwiczenia:
W doświadczeniu, wykorzystując monochromatory i przedstawiony powyżej układ, dokonujemy pomiaru potencjału hamowania (Vh) dla różnych długości fal. Na początku, przy wyłączonym źródle światła ustawiamy położenie zera w amperomierzu. Włączamy następnie źródło światła. Zwiększamy za pomocą potencjometru napięcie przyłożone do anody i katody fotokomórki, aż fotoprąd przestanie płynąć. Wskazywane wówczas przez woltomierz napięcie jest napięciem hamującym. Pomiary dla poszczególnych długości fali światła wykonujemy trzykrotnie w związku z dużym prawdopodobieństwem wystąpienia znaczących błędów wynikających z niedokładności odczytu, jak i niewłaściwej pracy układu pomiarowego (podczas ćwiczenia mierzymy prądy rzędu nanoamperów, więc wszelkie zakłócenia wpływają w poważnym stopniu na poprawność pomiarów). Zestawienie wyników przedstawia tabela 1.1 W drugiej części doświadczenia, dla dwóch długości fal, wykonujemy pomiary zależności mierzonego natężenia fotoprądu od napięcia pomiędzy anodą, a katodą. Napięcie zmieniamy od potencjału hamowania do maksymalnego.
III. Wyniki pomiarów i rachunek błędów.
Tabela 1.1 Pomiary napięcia hamującego (Vh) dla różnych długości fal
Lp. |
|
|
|
|
m |
1/s |
V |
1. |
0,0000006 |
5*1014 |
-0,46 |
2. |
0,00000058 |
5,17241*1014 |
-0,47 |
3. |
0,00000056 |
5,35714*1014 |
-0,52 |
4. |
0,00000054 |
5,55556*1014 |
-0,6 |
5. |
0,00000052 |
5,76923*1014 |
-0,67 |
6. |
0,0000005 |
6*1014 |
-0,77 |
7. |
0,00000048 |
6,25*1014 |
-0,89 |
8. |
0,00000046 |
6,52174*1014 |
-1 |
9. |
0,00000044 |
6,81818*1014 |
-1,12 |
10. |
0,00000042 |
7,14286*1014 |
-1,24 |
11. |
0,0000004 |
7,5*1014 |
-1,36 |
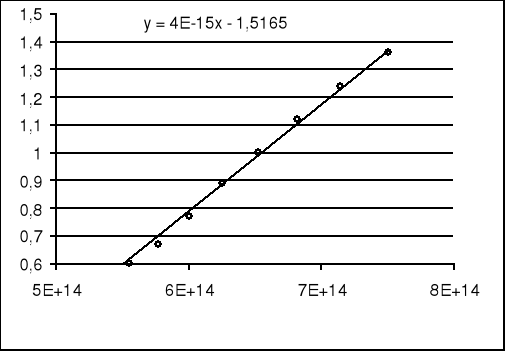
Na podstawie powyższej tabeli wykreślamy charakterystykę Vh = f (ν). Ponieważ wyniki pomiarów obarczone są błędami przypadkowymi tworzoną charakterystykę przybliżymy stosując metodę najmniejszych kwadratów - ( metoda przybliżania charakterystyk wykreślanych na podstawie wyników doświadczeń ).
Charakterystyka Vh = f ( ν) jest zależnością liniową wyrażającą się wzorem :
V=hν/e + W/e, gdzie h/e współczynnik kierunkowy „a” prostej , W/e - stała „b”
Przy pomocy metody najmniejszych kwadratów będziemy poszukiwać optymalnych wartości współczynników „a” i „b” prostej y = ax + b.
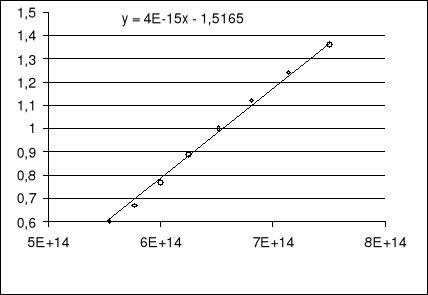
Wykres 1.1. Charakterystyka Vh(ν)
Dzięki tej metodzie obliczyliśmy stałą Plancka h i wartość pracy wyjścia które wynoszą:
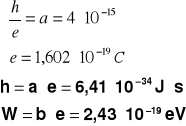
Δh = 3,21*10 -35
ΔW = 1,22*10 -20
Porównując otrzymaną wartość stałej Plancka z wartością tablicową możemy zauważyć, że otrzymana wartość niewiele odbiega od wartości tablicowej. Nasz wynik jest obarczony niewielkim błędem względnym około 5 %. Wynik ten jest do przyjęcia w naszej sytuacji a spowodowany jest błędami przypadkowymi w pomiarach wykonywanych przez mój zespół.
Biorąc po uwagę rozmiar błędu wyznaczenia tą metodą stałej Plancka możemy traktować ją jako metodę demonstracyjną, pozwalającą oszacować rząd stałej, która w żadnym razie nie może służyć do dokładnego określania stałej chyba, że wprowadzi się bardziej udoskonaloną metodę pomiaru mierzonych wielkości.
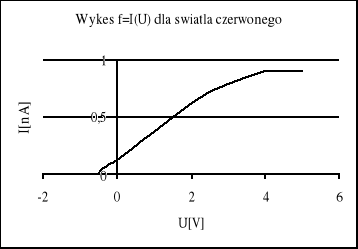
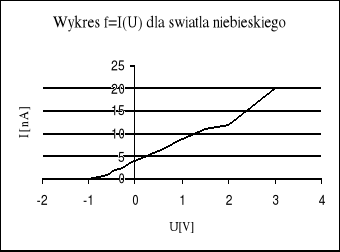
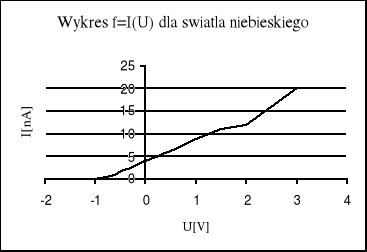
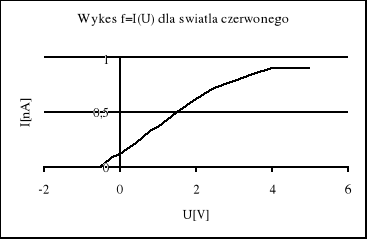
Pomiary charakterystyki f=I(U) dla światła niebieskiego (λ=460nm) przedstawia tablica 1.1, natomiast dla światła czerwonego (λ=660nm) tablica 1.2.
Tablica 1.1 Tablica 1.2
Uh [V] |
I [nA] |
|
Uh [V] |
I [nA] |
-1 |
0 |
|
-0,5 |
0 |
-0,89 |
0,24 |
|
-0,4 |
0,04 |
-0,78 |
0,5 |
|
-0,3 |
0,06 |
-0,71 |
0,66 |
|
-0,2 |
0,09 |
-0,60 |
0,96 |
|
-0,1 |
0,1 |
-0,46 |
1,8 |
|
0 |
0,12 |
-0,35 |
2,2 |
|
0,2 |
0,17 |
-0,24 |
2,6 |
|
0,4 |
0,22 |
-0,14 |
3,4 |
|
0,6 |
0,27 |
0 |
4 |
|
0,8 |
0,32 |
0,2 |
4,8 |
|
1 |
0,36 |
0,4 |
5,6 |
|
1,5 |
0,5 |
0,6 |
6,6 |
|
2 |
0,62 |
0,8 |
7,6 |
|
2,5 |
0,72 |
1 |
8,8 |
|
3 |
0,78 |
1,5 |
11 |
|
3,5 |
0,84 |
2 |
12 |
|
4 |
0,9 |
|
16 |
|
5 |
0,9 |
|
20 |
|
|
|
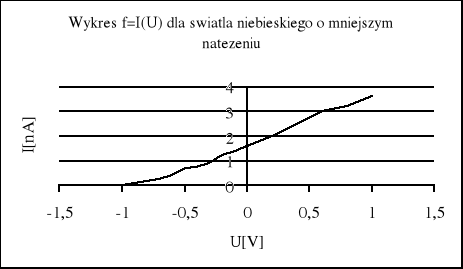
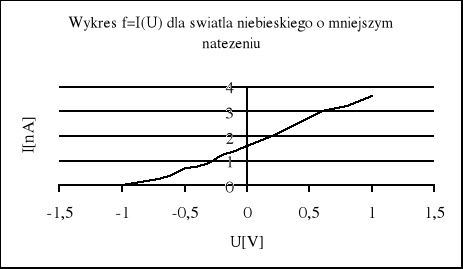
Charakterystykę f=I(U) dla światła niebieskiego o mniejszym natężeniu przedstawia tablica 1.3
Uh [V] |
I [nA] |
-1 |
0 |
-0,9 |
0,08 |
-0,8 |
0,18 |
-0,7 |
0,28 |
-0,6 |
0,42 |
-0,5 |
0,68 |
-0,4 |
0,74 |
-0,3 |
0,9 |
-0,2 |
1,2 |
-0,1 |
1,4 |
0 |
1,6 |
0,2 |
2 |
0,4 |
2,5 |
0,6 |
3 |
0,8 |
3,2 |
0,8 |
3,2 |
1 |
3,6 |
Powyższe wykresy charakterystyk prądowo napięciowych potwierdzają fakt, iż przy większym natężeniu światła następuje szybszy wzrost natężenia prądu w miarę wzrostu napięcia między anodą a katodą oraz wzrost natężenia prądu nasycenia, lecz nie ma zmiany potencjału hamowania okazuje się jednak przy pewnej wielkości potencjału występującego na fotokomórce następuje ustalenie się prądu przepływającego przez fotokomórkę.
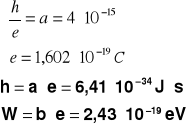
Wyszukiwarka
Podobne podstrony:
0 611 235 708 GBH 7 DE
0 611 222 703 GBH 4 DSC
611 Orędzie Żywego Płomienia Już za moment zatrzymam czas
0 611 228 703 GBH 2 24 DSR
0 611 238 703 GBH 2 24 DFR
0 611 218 703 GBH 2 24 DSR
611
611
611
611
44 611 624 Behaviour of Two New Steels Regarding Dimensional Changes
harm szkolen 611 po kl leg
avt 611 Alarm termiczny
611
610 611
611
611
2015 OR ćwid(611
więcej podobnych podstron