CIĄGŁOŚĆ FUNKCJI
Def. Mówimy, że funkcja jest ciągła w x0 jeżeli
Def. Mówimy, że funkcja jest ciągła w przedziale jeżeli jest ciągła w każdym punkcie tego przedziału
ODOSOBNIONY PUNKT NIECIĄGŁOŚCI
Def. Odosobnionym punktem nieciągłości nazywamy punkt x ∈ R, w którym funkcja nie jest ciągła, ale jest ciągła w (sąsiedztwie tego punktu) w pewnym zbiorze (x0 - δ, x0) ∪ (x0, x0 + δ).
KLASYFIKACJA PUNKTÓW NIECIĄGŁOŚCI
Def. Punkt nieciągłości odosobniony, nazywamy punktem nieciągłości pierwszego rodzaju jeżeli istnieje skończona granica jednostronna.
Def. Punkt nieciągłości odosobniony, nazywamy punktem nieciągłości drugiego rodzaju jeżeli choć jedna z granic jednostronnych nie istnieje lub jest granicą niewłaściwą.
WŁASNOŚCI FUNKCJI CIĄGŁYCH
Tw. Jeżeli funkcja ciągła w punkcie x0 spełnia warunek f (x0) > 0 lub f (x0) < 0, to istnieje przedział (x0 - δ, x0 + δ) w którym funkcja przyjmuje wartości (tylko) dodatnie (ujemne).
Tw. Funkcja ciągła w przedziale <a, b> przyjmuje wszystkie wartości leżące pomiędzy f (a) i f (b).
Tw. Funkcja ciągła w przedziale <a, b> przyjmuje w tym przedziale wartość najmniejszą i największą.
POCHODNA FUNKCJI
Def. Mówimy, że funkcja f ma pochodną w punkcie x0 jeżeli istnieje skończona granica:
Styczna do wykresu y=f(x) w (x0,f(x0)):
y - f(x0) =f' (x0) (x-x0)
RÓŻNICZKOWALNOŚĆ FUNKCJI
Tw. Funkcja różniczkowalna w punkcie x0 jest w tym punkcie ciągła
Przykład:
Nie istnieje pochodna w punkcie 0!
Tw. Jeżeli f i g są różniczkowalne to:
POCHODNA FUNKCJI ODWROTNEJ
Tw. Jeżeli f(x) jest rosnąca (malejąca), istnieje pochodna f `(a) ≠ 0 , jeżeli b= f (a) to f-1 (x) jest różniczkowalna w punkcie b oraz pochodna tej funkcji odwrotnej w punkcie b
Przykład:
POCHODNA FUNKCJI ZŁOŻONEJ
Tw. Jeżeli istnieje pochodna funkcji w punkcie x oraz istnieje pochodna funkcji f w punkcie g(x), to istnieje pochodna funkcji złożonej fog w punkcie x oraz (fog)'(x)=f'(g(x))*g'(x).
Przykład:
Przykład:
PRZEDSTAWIENIE PRZYROSTU FUNKCJI
Tw. Jeżeli dziedzina funkcji f zawiera pewne otoczenie (Ux0) punktu x0 oraz istnieje pochodna f ` (x0), to dla każdego h takiego, że x + h ∈ Ux0 zachodzi wzór:
f(x0+h)-f(x0)=f'(x0)*h+α(h)*h,
przy czym:
(x→0) lim α(h)=0.
RÓŻNICZKA FUNKCJI f W PUNKCIE X0
Def. df (x0) = f ' (x0) * h.
h = Δx
Def. df (x0) f ' (x0) * Δx
x→ df (x)
Przykład:
f (x0+h) ≈ f (x0) + f ' (x0) * h
więc h = 0,01
TWIERDZENIE DE L'HOSPITALA
Stosujemy tylko kiedy występuje symbol nieoznaczony)
Tw. (Z: - założenie)
są określone i różniczkowalne w
sąsiedztwie punktu x0 (Sx0).
Teza (T) Istnieje:
Przykład:
Przykład:
Przykład:
Przykład :(nieskończony)
ASYMPTOTY
Asymptoty pionowe:
Def. x = x0 jest asymptotą pionową lewostronną (prawostronną) jeśli:
Przykład:
x = 3 nie jest asymptotą pionową lewostronną
x = 3 jest as. pionową prawostronną.
Asymptoty ukośne:
Def. y = ax + b jest asymptotą ukośną f(x) w + ∞ (- ∞) jeżeli:
(x→∞) lim [ f(x) - ax + b)] = 0
Jeżeli istnieją skończone granice
to prosta y = ax + b jest asymptotą ukośną funkcji f(x) w + ∞ (- ∞).
Przykład:
y= x + 1 as. ukośna w +∞.
TWIERDZENIE ROLLE'A
Tw. Jeżeli funkcja jest ciągła w <a,b>, różniczkowalna w (a,b), oraz f(a) = f(b), to istnieje c ∈ (a,b) taki, że f ` (c) = 0.
Przykład:
Udowodnić, że równanie x3 - 3x + a = 0 nie może mieć 2 różnych pierwiastków ∈<0,1>. Załóżmy, że x1, x2 ∈ <0,1>, x1 ≠ x2 i x13 - 3x1 + a = 0
x23 - 3x2 + a = 0
f(x)= x3 - 3x + a
f(x1)=f(x2)=0
niech: x1 < x2
<x1,x2>
f ' (c) = 0
3c2 - 3 = 0 ⇔ c = ± 1
0 ≤ x1 < c < x2 ≤ 1 - sprzeczność
TWIERDZENIE LAGRANGE'A
Tw. Jeżeli funkcja jest ciągła w <a,b>, różniczkowalna w (a,b), to istnieje c ∈ (a,b), taki, że:
Wnioski:
1) funkcja jest funkcją stałą w (a,b) ⇔ f ` (x) = 0 w (a,b)
x1 < x2 ⇒ f (x1) = f (x2)
2) jeżeli f ` (x) > 0 w (a,b) to funkcja jest funkcją rosnącą
w (a,b) x1 < x2 ⇒ f (x1) < f (x2)
3) jeżeli f ` (x) < 0 w (a,b) to funkcja jest funkcją malejącą
w (a,b)
EKSTREMUM
Def. Funkcja ma w x0 maksimum (minimum) lokalne, jeżeli
- max. właściwe
Warunek konieczny (WK) na istnienie ekstremum lokalnego:
Jeżeli funkcja ma pochodną f ` (x0) i w x0 jest przyjęte ekstremum, x0 f ` (x) = 0
Warunek wystarczający ekstremum:
1) jeżeli funkcja jest różniczkowalna w Sx0, ciągła w x0 to:
jeżeli f ` (x) < 0 w Sx0-, f ` (x) > 0 w Sx0+, to funkcja ma w x0 minimum lokalne właściwe
jeżeli f ` (x) > 0 w Sx0-, f ` (x) < 0 w Sx0-, to funkcja ma w x0 minimum lokalne właściwe
2) jeżeli f ` (x0) = 0 to:
funkcja ma w x0 max lokalne właściwe, jeżeli f `' (x0) < 0
funkcja ma w x0 max lokalne właściwe, jeżeli f `' (x0) > 0
WKLĘSŁOŚĆ I WYPUKŁOŚĆ
Def. Funkcje f (x) nazywamy wypukłą (wklęsłą) w (a,b), jeżeli wykres tej funkcji w (a,b) znajduje się pod (nad) sieczną łączącą punkty (a, f (a)), (b, f (b))
∪ - wypukła, ∩ - wklęsła
Tw. Jeżeli f `' (x) > 0 w (a,b), to funkcja jest wypukła w (a,b)
Tw. Jeżeli f `' (x) < 0 w (a,b), to funkcja jest wklęsła w (a,b)
PUNKT PRZEGIĘCIA
Def. Punkt (x0 , f (x0)) jest punktem przegięcia funkcji f(x), jeżeli funkcja jest funkcją wklęsłą (wypukłą) w sąsiedztwie lewostronnym Sx-; wypukłą (wklęsłą) w sąsiedztwie prawostronnym Sx+.
CAŁKA NIEOZNACZONA
Def. Funkcję pierwotną funkcji f (x) na przedziale I nazywamy każdą różniczkowalną funkcję F(x) spełniającą warunek F'(x) = f (x)
f (x) = sin x F (x) = -cos x
Tw. Każda funkcja ciągła na przedziale I ma w tym przedziale funkcję pierwotną
-cos x + 3 (dodać dowolną stałą i zawsze otrzymamy
funkcję pierwotną)
Tw. Jeżeli F (x) jest funkcją pierwotną funkcji f (x) w przedziale I, to:
1) F(x)+ c , c∈R też jest funkcją pierwotną
2) Każdą funkcję pierwotną ∅(x) można przedstawić
w postaci ∅(x) = F (x) + c dla pewnego c∈R.
{F(x)+ c , c∈R}
Def. Całką nieoznaczoną funkcji f (x) na przedziale I nazywamy zbiór wszystkich funkcji pierwotnych funkcji f (x) na przedziale I.
Def. Funkcja dla której istnieje funkcja pierwotna nazywa się funkcją całkowalną.
Własności całki nieoznaczonej:
AD 2) f - całkowalna
AD 3) f, g - całkowalne
Przykład:
Przykład:
Przykład:
Przykład:
CAŁKOWANIE PRZEZ PODSTAWIANIE
Tw. Jeżeli funkcja t = ϕ (x) jest różniczkowalna w przedziale „i” oraz przekształca przedział „i” na przedział „j”, w którym funkcja f(t) jest całkowalna, to
Przykład:
Przykład:
CAŁKOWANIE PRZEZ CZĘŚCI
Tw. Jeżeli funkcje U(x) i V(x) mają ciągłe pochodne w przedziale I, to
Przykład:
FUNKCJE WYMIERNE
1) w(x) jest funkcją wymierną niewłaściwą, jeżeli k ≥ n
2) w(x) jest funkcją wymierną właściwą, jeżeli k < n
Każdą funkcję wymierną można przedstawić w postaci sumy wielomianu i funkcji wymiernej właściwej.
Przykład:
Ułamkiem prostym pierwszego rodzaju nazywamy funkcję wymierną w postaci
Ułamkiem prostym drugiego rodzaju nazywamy funkcję wymierną w postaci
Tw. Każdą funkcję wymierną właściwą można przedstawić w postaci sumy ułamków prostych
Przykład:
CAŁKA RIEMANA
Def. Jeżeli dla każdego ciągu podziałów normalnego, ciąg sum częściowych dąży do tej samej granicy, niezależnej od wyboru punktów pośrednich, to granicą tą nazywamy całką Riemana funkcji f w przedziale <a,b> i oznaczamy symbolem
Funkcja całkowalna w sensie Riemana w przedziale <a,b> to funkcja 0 której mówi się R-całkowalna
Tw. Każda funkcja ciągła w przedziale <a,b> jest w tym przedziale R-całkowalna
CAŁKI NIEWŁAŚCIWE
1) Całki niewłaściwe I-go rodzaju
Niech funkcja będzie określona w <a,∞) i całkowalna w sensie Riemana w każdym <a,b> dla b>a
Ta całka niewłaściwa jest zbieżna jeżeli ta granica istnieje i jest skończona. W pozostałych przypadkach ta całka jest rozbieżna.
2) Całki niewłaściwe II-go rodzaju
Niech funkcja będzie określona i nieograniczona w <a,b) i całkowalna w sensie Riemana w każdym przedziale <a,c> dla a < c < b
Jeżeli funkcja jest nieograniczona w (b,a>, całkowalna w (c,a>, a > c >b, to
Praca pochodzi z serwisu www.e-sciagi.pl
![]()
![]()
![]()

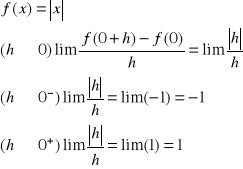

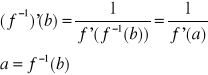
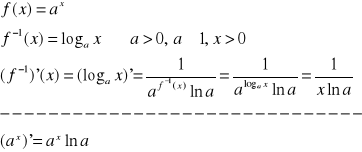



![]()
![]()
![]()
![]()
![]()

![]()

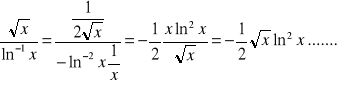
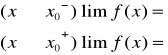
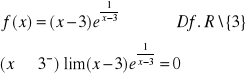

![]()

![]()




![]()


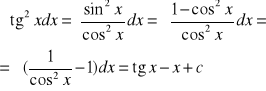
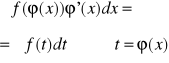


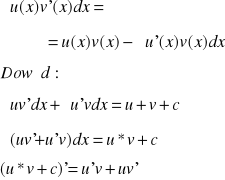
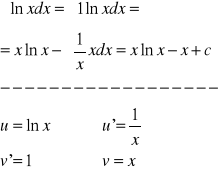

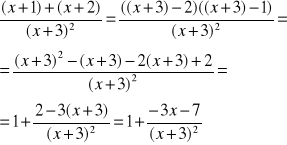
![]()
![]()



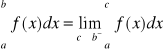
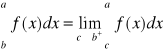
Wyszukiwarka
Podobne podstrony:
ściąga z matmy (ustny)2, INNE KIERUNKI, matematyka
ściąga z matmy (zadania), INNE KIERUNKI, matematyka
ściąga z matmy6 (zadania), INNE KIERUNKI, matematyka
ściąga z matmy2 (zadania), INNE KIERUNKI, matematyka
ściąga z matmy5 (zadania), INNE KIERUNKI, matematyka
ściąga z matmy7 (zadania), INNE KIERUNKI, matematyka
ściąga z matmy3 (zadania), INNE KIERUNKI, matematyka
ściąga z matmy (ustny)2
zagadnienia matematyczne, INNE KIERUNKI, matematyka
Matematyka finansowa - zadania 2, INNE KIERUNKI, matematyka
algorytmika i metody numeryczne - wykład, INNE KIERUNKI, matematyka
Matematyka finansowa - zadania, INNE KIERUNKI, matematyka
więcej podobnych podstron