Zadanie 1. Mamy figurę usytuowaną w zadanym układzie współrzędnych yz (rys. 1). Należy wyznaczyć jej charakterystyki geometryczne względem tych osi, korzystając z twierdzeń transformacyjnych i znajomości charakterystyk geometrycznych figur typowych. Dane: a. Szukane: S_y, S_z, y_C, z_C, I_y, I_z, I_yz.

Rozwiązanie

Rozwiązanie opracował dr inż. Dariusz Druzga (Politechnika Wrocławska, Wydział Budownictwa Lądowego i Wodnego, Instytut Inżynierii Lądowej, Zakład Wytrzymałości Materiałów).

Wszelkie prawa autorskie zastrzeżone. Korzystanie dozwolone - wyłącznie we własnym zakresie - przez osoby, które otrzymały opracowanie od autora.

1. Uwagi wstępne

Podana figura jest figurą złożoną, dlatego trzeba ją podzielić na figury prostsze - w tym przypadku można w niej wyodrębnić figury typowe. Podział figury złożonej na figury prostsze (na ogół typowe) jest krokiem rozpoczynającym rozwiązanie tego rodzaju zadania, jak tu prezentowane. Podział naszej figury pokazuje rys. 2. Figury typowe, składające się na tę figurę, to: prostokąt o podstawie a i wysokości 2a, półkole o promieniu a, oraz trójkąt prostokątny o podstawie 2a i wysokości a. Na tym etapie rozwiązywania tego rodzaju zadania ważne jest to, aby dokonać optymalnego podziału figury złożonej na figury prostsze. Należy figurę złożoną podzielić na najmniejszą ilość figur prostszych, niezbędną dla rozwiązania zadania. Zwiększanie ilości figur prostszych w podziale figury złożonej zwiększa ilość operacji obliczeniowych, jakie należy wykonać. To z kolei wydłuża czas rozwiązania zadania oraz zwiększa możliwość popełnienia błędu w obliczeniach.

Figury składowe numerujemy kolejnymi liczbami rzymskimi (piszemy je w kółku, co zwiększa czytelność oznaczenia). Ponieważ są to figury typowe, dla których znamy położenia środków ciężkości, to nanosimy te punkty dla każdej z nich (rys. 3) i oznaczamy je dużą literą C z dolnym indeksem w postaci cyfry rzymskiej, zastosowanej do oznaczenia danej figury składowej. Następnie rysujemy osie centralne (środkowe) tych figur, równoległe do osi zadanych. Osie centralne opisujemy tymi samymi literami, co osie zadane, do których są one równoległe, czyli za pomocą liter: y, z, przy czym dodatkowo litery te zaopatrujemy w dolne indeksy, będące oznaczeniami środków ciężkości, przez który osie przechodzą (C_I, C_II,…, itd.). Przykładowo - osie centralne figury składowej nr I - będą miały oznaczenia:
,
, gdzie:
||
i
||
(rys. 3).

O naszej figurze złożonej i figurach składowych, które w niej wyodrębniliśmy, możemy powiedzieć, że mają one ukierunkowanie zgodne z osiami zadanymi yz, gdyż boki czworokąta, średnica półkola oraz przyprostokątne trójkąta są równoległe do tych osi współrzędnych. Takie położenie tych figur powoduje, że do wyznaczania szukanych wielkości wystarczy zastosować tylko wzory transformacji translacyjnej, czyli twierdzenie Steinera (twierdzenie o osiach równoległych). Z tego powodu dla figur składowych narysowaliśmy te ich osie centralne, które są równoległe do osi zadanych.

Przy rozwiązywaniu tego rodzaju zadania korzystamy z zasady addytywności charakterystyk geometrycznych figur płaskich. W myśl tej zasady wartość szukanej wielkości danej figury złożonej jest sumą wartości tej wielkości, wyznaczonych dla figur składowych.

Momenty statyczne (S) i momenty bezwładnościowe (I) danej w zadaniu figury złożonej mają tylko dolne indeksy, którymi są oznaczenia osi zadanych (y i z) lub oznaczenia osi centralnych figur składowych (
,
,…,). Wielkości te nie muszą mieć indeksu górnego (jego brak jest w tym przypadku informacją, że chodzi o wielkość dotyczącą figury złożonej). Wielkości odnoszące się do figur składowych muszą mieć dodatkowo indeks górny. Informuje on o tym, której figury wielkość dotyczy i ma postać cyfry rzymskiej, którą oznaczona została rozpatrywana figura składowa.

2. Wyznaczenie momentów statycznych

Zgodnie z zasadą addytywności - momenty statyczne naszej figury względem osi y oraz osi z są sumą momentów statycznych figur składowych względem poszczególnych osi:

(1)
,

(2)
.

Momenty statyczne figur składowych względem poszczególnych osi wyrażają wzory:

(3)
,

(4)
,

Ze wzorów (2) i (3) wynika, że do wyliczenia szukanych wielkości potrzebne są:

1. y-owe współrzędne środków ciężkości figur składowych (dla wyliczenia momentów statycznych względem osi z), czyli:
   ,

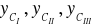
2. z-owe współrzędne środków ciężkości figur składowych (dla wyliczenia momentów statycznych względem osi z), czyli:
   ,

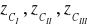
3. pola figur składowych (
   ).

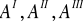
Wobec tego robimy zestawienie współrzędnych środków ciężkości i pół figur składowych:

(5)
,

(6)
,

(7)
.

Następnie wyliczamy momenty statyczne figur składowych, podstawiając do wzorów (3) i (4) odpowiednie wyrażenia przedstawione wzorami (5)-(7):

(8)
,

(9)

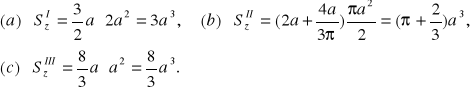
Teraz można wyliczyć momenty statyczne figury złożonej:

(10)
,

(11)
.

3. Wyznaczenie środka ciężkości

Współrzędne środka ciężkości
naszej figury wyznaczamy ze wzorów:

(12)
.

Wyliczmy najpierw pole A figury złożonej:

(13)

Współrzędne środka ciężkości wyliczamy ze wzorów (12):

(14)

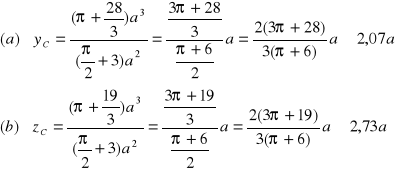
4. Wyznaczenie momentów bezwładności

W celu wyznaczenia momentów bezwładności danej figury złożonej korzystamy - tak jak przy wyznaczaniu momentów statycznych - z zasady addytywności: Jej zapis dla momentów bezwładności naszej figury przedstawiają wzory:

(15)
,

(16)
.

Dla wyznaczenia momentów bezwładności figur składowych korzystamy z twierdzenia Steinera, zapisanego dla tych figur poniżej:

(17)

(18)

Przykładowo - dla figury I i osi zadanej y - w myśl twierdzenia Steinera moment bezwładności tej figury względem tej osi jest równy sumie momentu bezwładności względem osi centralnej
(czyli osi centralnej równoległej do osi zadanej y) oraz iloczynu kwadratu odległości obu osi (
) i pola powierzchni tej figury (pole
). Jak widać - odległość pomiędzy tymi osiami wyznacza z-owa współrzędna środka ciężkości tej figury, czyli
.

Ogólnie twierdzenie Steinera dla momentów bezwładności jest następujące:

moment bezwładności danej figury względem zadanej osi jest równy sumie momentu bezwładności tej figury względem jej osi centralnej równoległej do osi zadanej oraz iloczynu kwadratu odległości między tymi osiami i pola tej figury.

Ze wzorów (17) i (18) wynika, że potrzebne są nam momenty bezwładności poszczególnych figur składowych względem ich osi centralnych. Ponieważ są to figury typowe, to korzystamy ze znanych dla tych figur wzorów, zapisanych poniżej:

(19)

(20)

Dodatkowego wyjaśnienia wymagają wzory (19b) i (20b). Wzór (19b) został wyznaczony przy znajomości momentów bezwładności ćwierćkola. Momenty bezwładności ćwierćkola o promieniu r (rys. 4), przylegającego bokami do pewnych zadanych osi ηζ. (osie: eta, dzeta) wynoszą:
Na rys. 4 ćwierćkole jest usytuowane w pierwszej ćwiartce układu współrzędnych, jednak podane wzory są takie same niezależnie od tego, w której ćwiartce układu współrzędnych będzie położone ćwierćkole. Wobec tego, jeżeli dopełnimy ćwierćkole z rys. 4 kolejnym ćwierćkolem, przylegającym bokami do układu współrzędnych w jego czwartej ćwiartce, to oba ćwierkola dają półkole (rys. 5), którego moment bezwładności względem zadanych osi ηζ jest - zgodnie z zasadą addytywności - sumą momentów bezwładności ćwiartek koła względem tych osi. Momenty bezwładności półkola względem zadanych osi η i ζ są zatem dwukrotnością momentów bezwładności ćwierćkola względem tych osi i wynoszą:
. W ten sposób doszliśmy do wzoru (19b).

W przypadku wyprowadzenia wzoru (20b) stosujemy twierdzenia Steinera dla półkola (rys. 5), korzystając ze znajomości jego momentu bezwładności względem osi ζ oraz odległości pomiędzy tą osią i osią centralną ζ_C, równą
. Zgodnie z twierdzeniem Steinera będziemy mieli:

(21)

Mamy już wszystkie potrzebne wielkości, zatem możemy wyliczyć momenty bezwładności poszczególnych figur składowych względem zadanych osi yz.

(22)

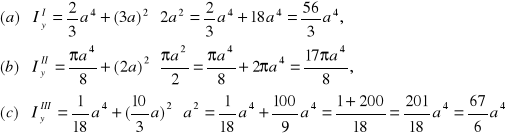
(23)

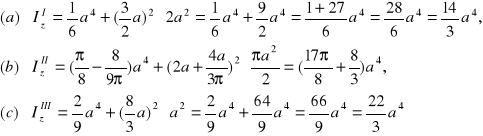
Wyliczamy teraz momenty bezwładności naszej figury złożonej względem zadanych osi yz:

(24)

(25)

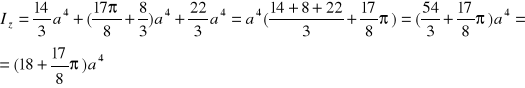
4. Wyznaczenie momentu dewiacji

Również przy wyznaczaniu momentu dewiacji zadanej figury złożonej korzystamy z zasady addytywności, co zapisujemy:

(26)
,

Momenty dewiacji poszczególnych figur składowych względem osi yz wyznaczamy z twierdzenia Steinera, jak poniżej

(27)

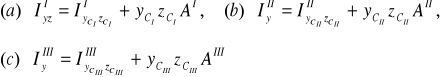
Teraz dla poszczególnych figur składowych można przystąpić do wyznaczania ich momentów dewiacji względem osi yz,. Jak widać ze wzorów (27) potrzebne są w tym celu momenty dewiacji tych figur względem ich osi centralnych (
, i=I, II, …,). Wyznaczamy je korzystając ze znajomości tych wielkości dla figur typowych. Na początku zauważmy, że w przypadku prostokąta oraz półkola (figury I i II) przynajmniej jedna z osi centralnych tych figur jest jej osią symetrii (w przypadku prostokąta obie osie, a w przypadku półkola - oś
). Jeżeli przynajmniej jedna z dwóch osi, względem których liczymy moment dewiacji danej figury jest jej osią symetrii, to moment dewiacji tej figury względem tych osi jest równy zeru. Opierając się na tej własności momentu dewiacji stwierdzamy, że momenty dewiacji względem osi centralnych prostokąta (osie

) i półkola (osie

) są równe zeru, czyli:

.

W przypadku trójkąta prostokątnego (figura III), jego moment dewiacji względem osi centralnych wynosi:

.

Znak minus we wzorze występuje dlatego, że trójkąt znajduje się w I ćwiartce układu współrzędnych yz.

Wykorzystując współrzędne środków ciężkości i pół figur składowych, wyrażonych wzorami (5)-(7), wyliczamy momenty dewiacji figur składowych:

(28)
,

(29)
,

(30)

Wyliczone wielkości wstawiamy do wzoru (26) i wyliczmy moment dewiacji podanej figury złożonej względem zadanego układu współrzędnych yz:

(31)
.

Wszystkie szukane wielkości zostały wyznaczone, co kończy wykonanie zadania.

Odpowiedź:
,
,
,
,
,
,
.

a

a

a

a

a

a

a

a

y

z

Rys. 1

III

III

III

I

Rys. 2

I

III

C_II

C_III

C_I

III

II

I

z

y

a

a

a

a

a

a

a

a

(
,
)

Rys. 4

(
,
)

(
,
)

III

Rys. 3

4r

3π

C

ζ_C

IV

III

II

I

ζ

η

IV

II

I

η

r

ζ

Rys. 5

r

---