ĆWICZENIE 11
(12.01.2009)
Energia sprężysta
J. German „Wykłady dla studiów dziennych” nr 11.
ZGINANIE ZE ŚCISKANIEM
Bodnar str. 206-210 „Skrypt dla studiów zaocznych”
Moment zginający : 
- pełne ugięcie belki,
- ugięcie pochodzące od obciążenia poprzecznego,
- ugięcie wywołane siłą N.
Pełne ugięcie w jest większe od sumy ugięć wywołanych oddzielnie działaniem obciążenia poprzecznego i siły N. Siła N powoduje jedynie powiększenie się ugięć od obciążenia poprzecznego. Zasada superpozycji nie obowiązuje. Jeśli siła N jest siła rozciągającą to powoduje zmniejszenie się ugięć od obciążenia poprzecznego.
Dla sztywnych belek moment Nw jest niewielki i można przyjąć 
tzn. pominąć wpływ siły podłużnej na przemieszczenia.
Dla belek o przeciętnej sztywności wpływ siły ściskającej N jest zazwyczaj znaczny i nie można go pominąć
Belka przęsłowa z obciążeniem poprzecznym skierowanym w jedną stronę i ściskana siłą N.
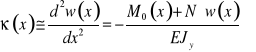
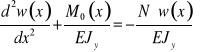
oznaczając:
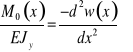
otrzymujemy:
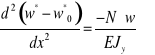
Dla uproszczenia przyjmujemy, że dodatkowe ugięcie 
zmienia się po długości belki wg sinusoidy, tzn.:
gdzie:
co prowadzi do równania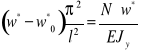 
i ostatecznie: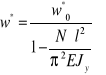 
Podstawiając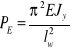 
otrzymujemy: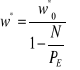 
Związek pomiędzy pełnym ugięciem 
a ugięciem 
wyraża się poprzez iloraz 
.
- kryterium sztywności belki ściskanej ze zginaniem poprzecznym.
- nie jest siłą krytyczną, lecz jedynie siłą obliczaną ze wzoru Eulera. Siłę krytyczną możemy obliczać jedynie dla smukłości większej od granicznej. Tutaj podstawiamy 
niezależnie od smukłości belki. Dalej we wzorze na Pkr występuje Jmin , a tutaj Jy względem głównej osi bezwładności prostopadłej do płaszczyzny działania obciążenia poprzecznego.
Gdy N=0 to mamy tylko zginanie poprzeczne 
|
|
0 |
0.5 |
0.6 |
0.7 |
0.8 |
0.9 |
0.95 |
1.0 |
|
|
1 |
2 |
2.5 |
3.33 |
5.0 |
10.0 |
20.0 |
∞ |
|
|
1 |
0.67 |
0.625 |
0.588 |
0.556 |
0.526 |
0.513 |
0.5 |
Zrobić wykres 
Ze względu na teorię małych przemieszczeń i przyjęcie krzywizny jako drugiej pochodnej ugięć wzór jest nieważny dla dużych ugięć. W rzeczywistości dla 
=1 
ugięcia mają wartość skończoną.
Naprężenia dla ściskania ze zginaniem obliczamy ze wzoru:
PRZYKŁAD LICZBOWY
L=12m
Przekrój: 
współczynnik bezpieczeństwa 
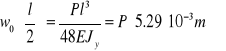
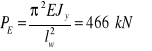
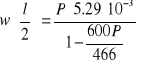
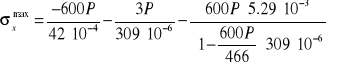
gdy 
Jeśli współczynnik bezpieczeństwa dla naprężeń wynosi 
to współczynnik bezpieczeństwa dla obciążeń wynosi 
Wnioski:
zależność 
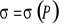
nieliniowa
takie belki należy obliczać względem obciążeń dopuszczalnych a nie naprężeń. 
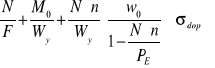
należy sprawdzić belkę na stateczność
zastosowanie wzoru empirycznego
