ĆWICZENIE 5

(18.11. i 25.11.)

KONWENCJA ZNAKOWANIA MOMENTÓW I WZÓR NA NAPRĘŻENIA

Wektor momentu przy zginaniu ukośnym można zrzutować na osie y, z , będące głównymi centralnymi osiami bezwładności przekroju. Przyjmujemy konwencję znakowania składowych momentów zgodnie z którą składowa jest dodatnia gdy jej zwrot jest zgodny z osią y lub z. Poniższy rysunek przedstawia składowe dodatnie.

Działanie poszczególnych składowych przedstawia rysunek. Rozciąganie włókien przedstawia kropka, ściskanie krzyżyk. Stąd dla pierwszej ćwiartki układu współrzędnych (dodatnie wartości współrzędnych y oraz z) wynikają odpowiednie znaki składników naprężeń normalnych:

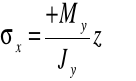
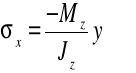
Dla zginania ukośnego momentem o dowolnych składowych otrzymujemy wzór zgodny z podaną konwencją znakowania.

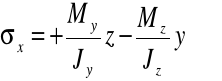
Uwaga: dla innej konwencji znakowania otrzymujemy inne znaki we wzorze na naprężenia.

Oś obojętna w przekroju zginanym ukośnie

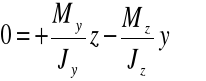
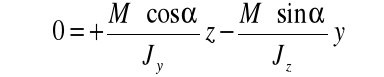
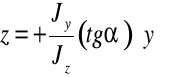
gdzie: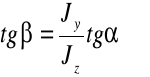

Przypadki:

PRZYKŁAD - SIŁA SKUPIONA

Wyznaczyć naprężenia w środku belki wolnopodpartej obciążonej siłą skupioną jak na rysunku poniżej przyłożoną w środku przęsła.

Z rysunku widać że składowe tej siły na oś y oraz na oś z są skierowane przeciwnie do odpowiednich osi.

Jeśli mamy do czynienia z obciążeniem przestrzennym (tzn. nie leżącym w żadnej z płaszczyzn wyznaczonej przez oś x i jedną z osi głównych) to najlepszą metodą jest rozkład tego obciążenia na dwie płaszczyzny
oraz
i analiza momentów zginających osobno dla każdej płaszczyzny a następnie zsumowanie składników naprężeń.

płaszczyzna
obciążenie składową

Poniżej przedstawiono wykres momentów, z którego należy odczytać wartość momentu w środku przęsła oraz przypisać znak. Znak ustalamy następująco: dokonujemy podziału płaszczyzną o normalnej zewnętrznej skierowanej zgodnie z osią x. Moment zginający działa ciągnąc włókna po tej stronie, po której narysowany jest wykres, w stronę włókien przeciwnych. Tak narysowanemu momentowi (na czerwono) przypisujemy wektor, zgodnie z reguła śruby prawoskrętnej. Jeśli ten wektor ma zwrot zgodny z osią układu prawoskrętnego (w tym przypadku oś z) to moment ten ma znak dodatni.

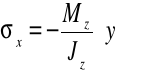
gdzie: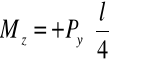

płaszczyzna
obciążenie składową

Analizując podobnie otrzymujemy wektor momentu przeciwny do osi Y

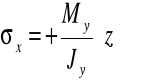
gdzie: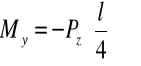

Naprężenie całkowite wyznaczamy ze wzoru dla zginania ukośnego:

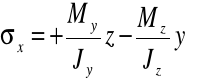
Dla zadania:

gdzie: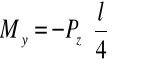
,

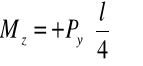
PŁATEW DACHOWA OBCIĄŻONA CIĘŻAREM WŁASNYM

SPOSÓB I

Obciążenie leży w płaszczyźnie xyo , która nie jest związana z osią główną. Jest możliwe narysowanie wykresu momentów Mzo oraz wyznaczenie wartości ekstremalnej wraz ze znakiem. Znak ustalamy następująco: dokonujemy przecięcia osi płaszczyzną normalną i zwracamy się na stronę, gdzie zwrot normalnej zewnętrznej jest zgodny z osią x. Moment (zgodnie z umową o rysowaniu momentów po stronie włókien rozciąganych) ciągnie w tym przypadku włókna dolne a ściska górne. Wektor momentu jest skierowany przeciwnie do osi zo . Wektor ten rozkładamy na składowe wzdłuż osi y oraz z otrzymując wartości tych składowych oraz znaki poprzez porównanie zwrotów wektorów składowych i zwrotów osi.

SPOSÓB II

Rozkład obciążenia q na składowe wzdłuż kierunków osi głównych przekroju. Rozważamy teraz dwie płaszczyzny xy oraz xz . W każdej z tych płaszczyzn rysujemy wykresy momentów zginających i podobną metodą jak poprzednio przypisujemy odpowiednim momentom znaki porównując zwroty osi prostopadłych do płaszczyzny oraz zwroty momentów. Otrzymujemy w ten sposób dwie składowe momentu zginającego, który otrzymamy przez złożenie tych składowych.

Nietrudno zauważyć ,że rezultat jest ten sam dla obydwu sposobów.

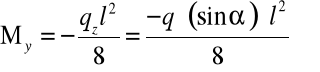
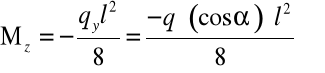
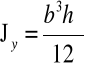
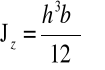
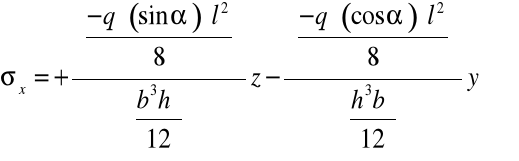
Oś obojętna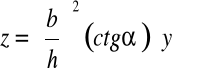

Dane do obliczeń:

Wyniki:

Zginanie ukośne

Zadanie.

Obliczyć maksymalne naprężenie normalne w belce jak na rys.1a. o przekroju jak na rys. 1b.

Rys.1a. Rys.1b.

kątownik
dane z tablic kształtowników:

I) Charakterystyki geometryczne przekroju

Przekrój posiada oś symetrii, co determinuje położenie głównych centralnych osi bezwładności
pod kątem 45 stopni względem osi ciężkości

Z prawa transformacji główne centralne momenty bezwładności wynoszą:

II) Naprężenia normalne w przekroju maksymalnego momentu zginającego:

Rozkładamy wektor momentu na składowe wzdłuż kierunków głównych:

Rozkład naprężeń normalnych w przekroju maksymalnego momentu określa równanie:

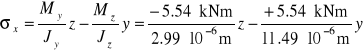
po podaniu współrzędnych yz punktów w metrach ze wzoru otrzymamy naprężenia mierzone w kPa.

Równanie osi obojętnej otrzymujemy z równania:

oś tą zaznaczono na poniższym rysunku

punkt A

Maksymalne naprężenie normalne występuje w punkcie przekroju najbardziej oddalonym od osi obojętnej. Z rysunku widać, że jest to punkt A o współrzędnych:

W celu wyznaczenia współrzędnych w układzie yz trzeba wykorzystać wzory transforma-cyjne przy obrocie układu:

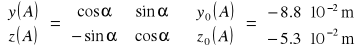
Naprężenie w punkcie A wynosi:

Zadanie

Wspornik o przekroju dwuteowym pokazanym na rys.3. zaprojektowany został na działanie siły poprzecznej. Wskutek niedokładności montażowej oś główna centralna przekroju odchyliła się od pionu o kąt
.Poszukać położenia osi obojętnej i porównać z położeniem osi obojętnej dla pręta idealnie zamontowanego. Dane:

Współrzędne momentu zginającego (dla przekroju przypodporowego) w głównych centralnych osiach bezwładności przekroju wynoszą:

rys.3.

Oś obojętną określa równanie:

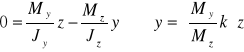
Po wstawieniu składowych momentów i wartości zadanego współczynnika k otrzymamy :

określa położenie nowej osi obojętnej.

Dla pręta idealnie zamontowanego oś z jest osią obojętną.

PROJEKT 5

Projektowanie płatwi dachowej - przykład.

Schemat po lewej stronie przedstawia rozkład obciążenia wzdłuż osi belki. Po prawej stronie przedstawiono kierunki obciążeń zewnętrznych oraz orientację przekroju względem kierunku poziomego (i pionowego)

Poniżej podany jest przekrój zwymiarowany parametrycznie.

Należy zaprojektować parametr a ze względu na maksymalne naprężenia normalne, występujące w przekroju α-α . Narysować oś obojętną w tym przekroju oraz bryłę naprężeń.

---