ĆWICZENIE 10

(6.01.2009)

Materiał idealnie sprężysto-plastyczny - na korzyść bezpieczeństwa

NOŚNOŚĆ GRANICZNA

Definicja. Obciążenie nośności sprężystej - największe obciążenie, przy którym cała konstrukcja pracuje jeszcze w stanie sprężystym.

Definicja. Wartość obciążenia, przy którym konstrukcja traci zdolność jego przenoszenia w wyniku takiego uplastycznienia przekrojów, że ustrój staje się geometrycznie zmiennym nazywamy nośnością graniczną. (zamiana konstrukcji w mechanizm)

Jeśli podstawą projektowania jest stan nośności granicznej to mówimy o wymiarowaniu metodą nośności granicznej.

OSZACOWANIE NOŚNOŚCI GRANICZNEJ I METODY TEORII NOŚNOŚCI GRANICZNEJ

METODA STATYCZNA

Twierdzenie statyczne o oszacowaniu nośności granicznej od dołu.

Każdy statyczny mnożnik obciążenia jest mniejszy lub co najmniej równy rzeczywistemu mnożnikowi obciążenia granicznego

METODA KINEMATYCZNA

Twierdzenie kinematyczne o oszacowaniu nośności granicznej od góry.

Każdy kinematyczny mnożnik obciążenia jest większy lub co najwyżej równy rzeczywistemu mnożnikowi obciążenia granicznego

lub postać równoważna

Konstrukcja idealnie plastyczna ulegnie zniszczeniu pod działaniem danego obciążenia , jeśli można znaleźć taki mechanizm zniszczenia , dla którego moc obciążeń zewnętrznych nie jest mniejsza od mocy sił wewnętrznych.

KONSTRUKCJE

• Kratownice statycznie wyznaczalne (nośność sprężysta równa nośności granicznej)

• Kratownice statycznie niewyznaczalne (nośność sprężysta mniejsza lub równa granicznej - rozwiązanie metodą statyczną)

• Belki statycznie wyznaczalne (nośność sprężysta mniejsza lub równa granicznej - rozwiązanie metodą kinematyczną)

• Belki statycznie niewyznaczalne (nośność sprężysta mniejsza lub równa granicznej - rozwiązanie metodą kinematyczną)

gdy momenty statyczne liczone są względem głównych osi centralnych

lub

gdy momenty statyczne liczone są względem osi plastycznej (liczy się łatwiej)

BELKI STATYCZNIE WYZNACZALNE

Poszukujemy takiego mnożnika podanego okładu obciążenia
, dla którego konstrukcja zamienia się w mechanizm.

Do tej zamiany wystarczy uplastycznienie jednego przekroju, a mianowicie tego dla którego moment ma wartość ekstremalną. Wykres pokazuje że jest to punkt przypodporowy.

Charakterystyki geometryczne:

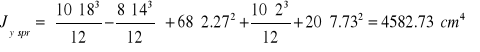
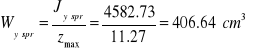
Położenie osi plastycznego zginania:

równe pola

Zapas nośności

BELKI STATYCZNIE NIEWYZNACZALNE

METODA STATYCZNA

Belka jest jednokrotnie statycznie niewyznaczalna. Aby konstrukcja zamieniła się w mechanizm potrzeba utworzenia dwóch przegubów plastycznych.

Pierwszy schemat statycznie dopuszczalny.

Zakładamy pierwszy przegub w utwierdzeniu i poszukujemy miejsca powstania drugiego.

W utwierdzeniu zakładamy wartość momentu uplastyczniającego przekrój, (konstrukcja staje się statycznie wyznaczalna) i rysujemy wykres momentów zginających.

Jeśli
to
oraz

schemat statycznie niedopuszczalny

Jeśli
to
oraz

Drugi schemat statycznie dopuszczalny.

Zakładamy pierwszy przegub w połowie belki i poszukujemy miejsca powstania drugiego.

Trzeci schemat statycznie dopuszczalny.

Zakładamy pierwszy przegub w ¾ belki i poszukujemy miejsca powstania drugiego.

Prawdziwy jest mnożnik obciążenia dla schematu dającego wartość maxymalną

METODA KINEMATYCZNA (dla belek częściej stosowana)

Zasada prac wirtualnych - układ ciał sztywnych znajduje się w równowadze jeśli praca sił zewnętrznych i wewnętrznych na przemieszczeniach wirtualnych jest równa zero.

Rysujemy możliwe schematy zniszczenia. Rozważana belka zamieni się w mechanizm po powstaniu 2 przegubów plastycznych. Wykres momentów zginających obciążonej siłami skupionymi jest w postaci linii łamanej, więc mamy następujące możliwe schematy zniszczenia.

1)

2)

3)

4) schemat mało prawdopodobny

Prawdziwy jest mnożnik obciążenia dla schematu dającego wartość minimalną

Jeżeli podstawą projektowania jest stan nośności granicznej to mówimy o wymiarowaniu metodą nośności granicznej.

Str 323 Piechnik . przykład na metodę kinematyczną

Przykład na kartkówkę:

METODA STATYCZNA (częściej stosowana dla kratownic)

Zwiększamy obciążenie kolejno wywołując stany sprężysty, sprężysto-plastyczny , aż do stanu zniszczenia.

α

1. zakładamy uplastycznienie pręta 1
   

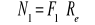
Równania równowagi węzła:

Schemat jest statycznie dopuszczalny gdy :

2) zakładamy uplastycznienie pręta 2

Równania równowagi węzła:

Schemat jest statycznie dopuszczalny gdy :

3) zakładamy uplastycznienie pręta 3

Schemat statycznie niedopuszczalny

Ostatecznie otrzymujemy:

ĆWICZENIE

Wyznaczyć zakres strefy plastycznej po wyczerpaniu się nośności plastycznej belki.

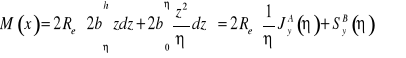
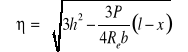
dla

Obliczenie

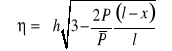
dla

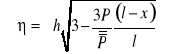
Gdy

zasięg

Przykład

schemat zniszczenia:

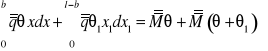
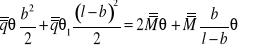
nie spełnia warunków zadania

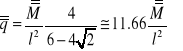
Zadanie.

Określić nośność plastyczną belki .

oś obojętna:

Możliwe kinematyczne schematy zniszczenia

możliwe schematy statyczne:

METODA KINEMATYCZNA

Dla danego układu określić nośność sprężystą i nośność graniczną, jeżeli granica plastyczności wynosi
oraz:
,
,
.

jednakowe dla wszystkich prętów.

Określenie nośności sprężystej.

1) Równania geometryczne (nierozdzielności)

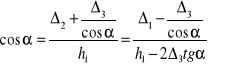
1)

2. równania fizyczne (prawo Hooke'a)

3. równania równowagi (statyka)

dla założonych wydłużeń działają na węzeł odpowiadające im siły.

Ponieważ
, więc możemy równanie geometryczne zapisać:

1)

1*)

Rozwiązując układ 1*) 2) 3) otrzymujemy siły:

,
,

otrzymujemy , dla jakiej siły P uplastycznią się poszczególne pręty.

,

,

Nośność sprężysta jest równa najmniejszej z wyliczonych wartości P:

Określenie nośności granicznej - podejście statyczne.

Rozważamy wszystkie możliwe (statycznie dopuszczalne) schematy zniszczenia: najpierw uplastycznia się jeden z prętów i konstrukcja, która była jednokrotnie statycznie niewyznaczalna, nie ulegnie jeszcze zniszczeniu. Zamiana w mechanizm następuje dopiero po uplastycznieniu następnego pręta. Powstanie wtedy mechanizm kinematyczny. Tak więc w tym przypadku o nośności granicznej decyduje uplastycznienie się dwóch kolejnych prętów. Jeżeli założymy uplastycznienie się pierwszego pręta, to konstrukcja staje się statycznie wyznaczalna i siły w prętach można obliczyć (przy zadanym obciążeniu) z równań statyki.

Możliwych jest 2*6=12 przypadków szczególnych: 6 przypadków uplastycznienia się 2 prętów z 3, przy czym siły w prętach mogą mieć znaki + lub -.

L.P.				P	uwagi
1	62.5	37.5	92.85	9.285	P=9.285
2	62.5	-37.5	23.21	37.14	P=37.14
3	62.5	45.2	100	6.425	>
4	62.5	-170.2	-100	86.425	>
5	-62.5	37.5	-23.21	-37.14	P<0
6	-62.5	-37.5	-92.85	-9.285	P<0
7	-62.5	170.2	100	-86.425	> , P<0
8	-62.5	-45.2	-100	-6.425	> , P<0
9	70.2	37.5	100	12.145	>
10	-145.2	37.5	-100	-67.855	> , P<0
11	145.2	-37.5	100	67.855	>
12	-70.2	-37.5	-100	-12.145	> ,P<0

Istnieją 3 możliwości:

1. założony schemat jest bardziej korzystny niż w rzeczywistości - otrzymuje się wtedy przekroczenie w pozostałym pręcie siły uplastyczniającej, co jest statycznie niedopuszczalne (przypadki 3,4,7,8,9,10,11,12).

2. założony schemat jest mniej korzystny niż w rzeczywistości - otrzymujemy wtedy oszacowanie nośności granicznej os dołu (przypadek 1)

3. założony schemat jest właściwy - przypadek 2.

Z rozwiązań odrzucamy przypadki, dla których P<0, co nie spełnia warunków naszego zadania (przypadki 5,6,7,8,10,12),

Tak więc nośność graniczna
.

Zapas nośności:
(wzrost o 14.3%)

---