Rogoziński Marcin Rzeszów dn. 03.04.2000 r.

Wydział Elektryczny

Temat: Badanie widma emisyjnego gazów. Wyznaczanie nieznanych długości fali.

Zagadnienia do samodzielnego opracowania.

1. Równania Maxwella jako podstawa matematycznego opisu propagacji fal elektromagnetycznych.

2. Model atomu w teorii klasycznej.

3. Rodzaje widm ze szczególnym uwzględnieniem widm liniowych.

Wykonanie ćwiczenia.

1. Połączyć obwód według schematu. Przed uruchomieniem przyrządów zgłosić się do prowadzącego ćwiczenia, aby w jego obecności włączyć induktor i ustawić układ tak, by na matówce w okularze lunety spektrometru oglądać intensywne widmo liniowe na tle oświetlonej (z zewnętrznego źródła) wskazówki połączonej z bębnem skali spektrometru.

2. Przesuwając bęben skali spektrometru, odczytać położenie L wszystkich linii widmowych.

3. Z tabeli odczytać długości fal λ_He zaobserwowanych linii gazu wzorcowego, którym jest hel.

Lp.	λHe[μm]	Barwa
1.	0,4026	fiolet
2.	0,4111	fiolet
3.	0,4388	fiolet
4	0,4471	niebieska
5.	0,4713	niebieska
6.	0,4922	niebiesko-zielona
7.	0,5016	zielona
8.	0,5878	żółta
9.	0,6678	czerwona
10.	0,7065	czerwona

4. Wykreślić krzywą dyspersji spektrometru
   .

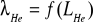
5. Zmienić rurkę Plückera na wypełnioną innym gazem, dającą inne widmo liniowe. Na podstawie wykreślonej krzywej dyspersji znaleźć długości fali linii wskazanych przez prowadzącego ćwiczenia.

Schemat układu

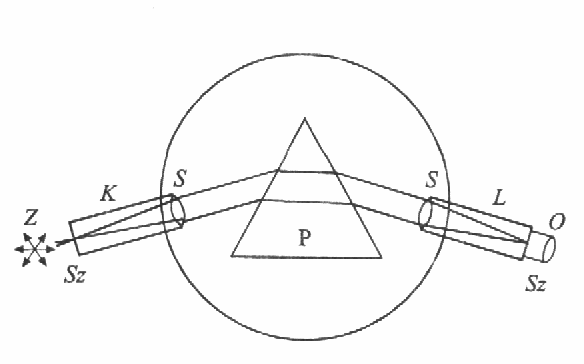
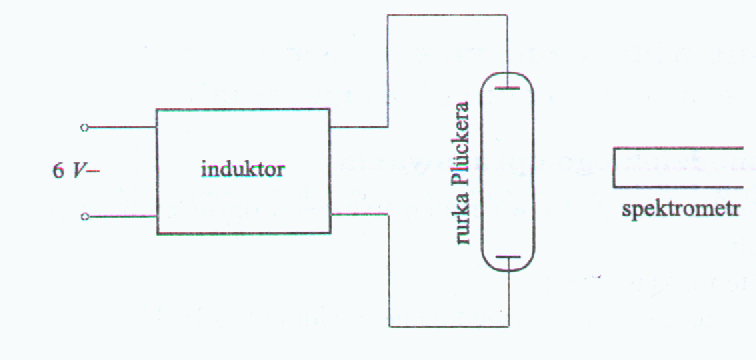
Schemat spektrometru

Tabela Pomiarowa

Lp.	Barwa linii	LHe	ΔL	λHe [ μm]	LH	Barwa linii	ΔλH [ μm]	λH [ μm]	λH±ΔλH [ μm]
1	fiolet	68.1		0.411	81.3	fiolet	0.071	0.443	0.443±0.071
2	fiolet	74.4		0.4388	85.1	fiolet	0.075	0.448	0.448±0.075
3	niebieski	89.65		0.4471	87.75	fiolet	0.075	0.453	0.453±0.075
4	niebiesko-zielony	100.8		0.4922	90.15	niebiesko-zielony	0.077	0.456	0.456±0.077
5	zielony	105.15		0.5016	101.3	zielony	0.059	0.493	0.493±0.059
6	zielony	106.6		0.516	105	zielony	0.054	0.504	0.504±0.054
7	żółty	135.1		0.5878	133.4	żółty	0.007	0.583	0.583±0.007
8	czerwony	152.6		0.6678	134.1	żółty	0.003	0.588	0.5880.003
9	czerwony	158.4		0.70065	135.5	pomarańczowy	0.0035	0.5895	0.5895±0.0035
10					136.6	pomarańczowy	0.001	0.593	0.593±0.001
11					138.8	czerwono-pomarańczowy	0.014	0.599	0.599±0.014
12					141.2	czerwony	0.012	0.61	0.61±0.012
13					150.5	czerwony	0.043	0.648	0.648±0.043

Obliczenia:

Wzór Hartmanna :

Podstawiam zmienne :

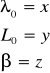
Przekształcam wzór:

Obliczam układ trzech równań z trzema niewiadomymi :

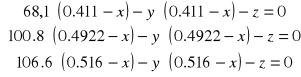
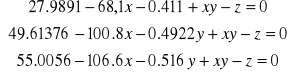
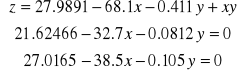
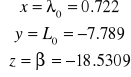
Obliczam długość fali ze wzoru Hartmanna oraz dokładność długości fali:

1. dla L_H=81.3

2. dla L_H=85.1

3. dla L_H=87.75

4. dla L_H=90.15

5. dla L_H=101.3

6. dla L_H=105

7. dla L_H=133.4

8. dla L_H=134.1

9. dla L_H=135.5

10. dla L_H=136.6

11. dla L_H=138.8

12. dla L_H=141.2

13. dla L_H=150.5

---