Temat: Polaryzacja fotonu

Nowa interpretacja doświadczeń nad polaryzacją światła

Rozpatrzymy spolaryzowaną falę płaską o długości λ, częstości
i wektorze falowym
rozchodzącą się w obszarze
przestrzeni o objętości V. Długości
,
charakteryzujące obszar
są znacznie większe od λ:
. Wkład pola elektrycznego do energii fali (1.6b) rozchodzącej się w
równy jest

.

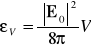
Wybierzemy układ współrzędnych x, y, z||
. Orientację osi x i y zwiążemy z polaryzatorem (np. polaroidem). Niech oś x tego układu będzie równoległa do kierunku przepuszczania polaryzatora (będziemy go nazywali analizatorem x). Zatem oś y układu współrzędnych jest skierowana równolegle do osi zatrzymywania polaroidu. Przypuśćmy, że przepuszczamy przez nasz analizator-x falę płaską liniowo spolaryzowaną pod kątem 45^o do osi x. Wektor Jonesa
pod wpływem analizatora x ulega przekształceniu

.

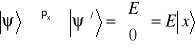
tzn.
. Gęstość energii fali przepuszczonej jest dwukrotnie mniejsza od gęstości energii wiązki wychodzącej. Wektor pola elektrycznego fali wychodzącej jest równoległy do osi x, czyli fala przepuszczona jest liniowo spolaryzowana w kierunku x, o czym można się przekonać ponownie przepuszczając ją przez analizator x.

Zgodnie z mechaniką kwantową
- energia fali rozchodzącej się w obszarze
jest wielokrotnością kwantu energii fotonu

.

Oczywiście N jest liczbą fotonów znajdujących się w obszarze
. Po przejściu przez analizator x

.

To oznacza, że połowa fotonów przechodzi przez nasz układ, a połowa zostaje odrzucona. Jednak fotony są identyczne i każdy z nich jednakowo oddziałuje z polaroidem. Jesteśmy zmuszeni przyjąć, że foton liniowo spolaryzowany w kierunku 45^o przechodzi przez ana­lizator x z prawdopodobieństwem ½ i z takim samym prawdopodobieństwem zostaje zatrzy­many. Konsekwencją takiej konkluzji jest istnienie fluktuacji liczby fotonów przepuszczo­nych i fluktuacji liczby fotonów zatrzymanych. Dla rozważanego przykładu liczby te fluktuują dookoła N/2. W granicy
iloraz
. Taka granica oznacza przejście od układu kwantowego (mikroskopowego) do klasycznego (makroskopowego). Po przejściu przez analizator x klasyczna wiązka spolaryzowana pod kątem 45^o ulega dwukrot­nemu osłabieniu.

Gdy przez analizator x przechodzi spolaryzowana fala płaska o wektorze E₀, któremu odpowiada wektor stanu
, iloraz

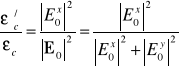
. (8.1a)

będziemy utożsamiali z prawdopodobieństwem
przejścia fotonu o polaryzacji
przez analizator x [1]. Gdy
to
, natomiast gdy przez analizator x przechodzi fala spolaryzowana pod kątem
do osi x to
to

.

Po przejściu przez analizator x każdy foton jest spolaryzowany liniowo w kierunku x, tj. prawdopodobieństwo napotkania wśród fotonów wychodzących z analizatora x fotonu inaczej spolaryzowanego znika. Układ jedynie nie zmienia stanu polaryzacji fotonów spolaryzowanych liniowo w kierunku x - czyli stanu własnego (6.10c) operatora
, polaryzacja wszystkich inaczej spolaryzowanych fotonów ulega zmianie.

Rozważymy falę o amplitudzie
odpowiadającej jednemu fotonowi w obszarze
, wtedy

.

Zdefiniujemy w bazie kartezjańskiej związanej z analizatorem x składowe
wektora stanu
fotonu spolaryzowanego

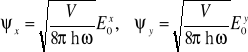
. (8.2a)

Zatem

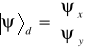
. (8.2b)

Zbadamy normę wektora
. Na podstawie równania (8.2a) stwierdzamy, że

.

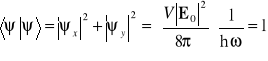
Jak widać wektory stanu polaryzacji fotonu są równoważne unormowanym do jedności wektorom Jonesa. Każdy unormowany do jedności wektor Jonesa można rozłożyć według wektorów dowolnej bazy ortogonalnej
(por. § 2.2)

. (8.3)

W mechanice kwantowej przyjmuje się, że relacja (8.3) jest słuszna nie tylko dla wektorów stanu polaryzacji ale i dla wektorów stanu innej natury. Z tego powodu relacja (8.3) nosi nazwę zasady superpozycji [1]. Uważana jest ona za podstawową zasadę mechaniki kwantowej.

Zapiszemy prawdopodobieństwo (8.1a) przy pomocy składowych
. Mnożąc licznik i mianownik wzoru (8.1a) przez czynnik
, otrzymamy

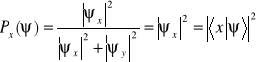
. (8.1b)

Iloczyn skalarny
nazywamy amplitudą prawdopodobieństwa zdarzenia polegającego na tym, że foton w stanie polaryzacji
zachowuje się jak foton będący w stanie
- tj. jak foton, który przechodzi przez analizator x. Natomiast
jest prawdopodobieństwem tego zdarzenia. W ogólnym przypadku iloczyn skalarny
jest amplitudą prawdopodo­bieństwa zdarzenia polegającego na tym, że foton w stanie
zachowuje się jak foton w sta­nie
. Rzecz jasna można uważać, że to foton w stanie
zachowuje się jak foton w stanie
.

8.2 Moment pędu światła spolaryzowanego

Za Feynmanem [2] pokażemy, że wiązka światła kołowo spolaryzowana niesie moment pędu. Wyprowadzenie ma charakter heurystyczny. Rozważymy wiązkę światła spolaryzowanego kołowo o wektorze Jonesa

.

Niech światło to pada prostopadle na powierzchnię ścianki pochłaniającej fotony. Jak wiemy ścianki składają się z atomów, które będziemy traktowali jak klasyczne trójwymiarowe oscylatory harmoniczne, które mogą zostać pobudzone do drgań przez zewnętrzne, oscylujące pole elektryczne, w naszym przypadku pole elektryczne fali. Ze względu na izotropowość możemy przyjąć, że pobudzone przez kołowo spolaryzowaną falę elektrony atomów poruszają się po wielkich okręgach kul. Okręgi te leżą w płaszczyźnie stałej fazy, a elektrony wirują z częstością kołową
. Przyjmijmy, że wszystkie te okręgi mają jednakowe pro­mienie równe r.

Obliczymy pracę wykonaną przez pole elektryczne fali nad elektronem. Niech E_t bę­dzie składową wektora pola styczną do okręgu, po którym z prędkością
porusza się elektron (Rys. 8.1). Praca wykonana nad elektronem w jednostkowym interwale czasu
równa jest

. (8.4a)

Rys. 8.1

Pochłanianiu energii przez atom towarzyszy zmiana momentu pędu. Zmiana z-towej składowej momentu pędu atomu
w jednostkowym interwale czasu związana jest z momentem siły
działającym na elektron

. (8.4b)

Zwiążemy zmianę
z pochłoniętą energią

. (8.5)

Z drugiej strony zmiana energii wiązki
związana jest ze zmianą
liczby fotonów wią­zki, które zostały pochłonięte

. (8.6)

Ze wzoru (8.5) i (8.6) wynika, że

. (8.6)

Jak widać każdy foton kołowo spolaryzowany prawostronnie niesie moment pędu
. Podobnie można pokazać, że foton lewostronnie spolaryzowany niesie moment pędu
.

Powrócimy do macierzy obrotu
w postaci (6.10b). Wprowadzimy operator mo­mentu pędu fotonu
. W wybranym przez nas układzie współrzędnych ma on tylko jedną nieznikającą składową

. (8.7a).

W bazie
macierz reprezentująca operator momentu pędu fotonu ma dobrze nam znaną postać

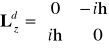
. (8.8a)

Macierz reprezentująca operator
w bazie x, y jest jedną z trzech macierzy Pauliego

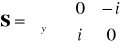
. (8.7b)

Pozostałymi macierzami Pauliego są

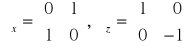
. (8.7c,d)

Natomiast w bazie stanów własnych
ma ona prostszą postać

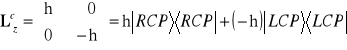
. (8.8a)

Gdy foton zostaje pochłonięty przez materię jej moment pędu powiększa się albo pomniejsza się o
. Nie zaobserwowano innych zmian. Gdy foton znajduje się w stanie
, różnym od kołowo spolaryzowanego, to z prawdopodobieństwem
zaobserwujemy wzrost momentu pędu materii o
, natomiast z prawdopodobieństwem
zaobserwujemy zmniejszenie jej momentu pędu o
. Załóżmy, że wykonano wiele doświadczeń na pochłanianiem fotonów w stanie
, przeprowadzone je w tych samych warunkach. Po uśrednieniu otrzymanych wyników stwierdzimy, że obserwowana jest następująca zmiana momentu pędu materii
równa

.

Zapiszemy
w innej postaci

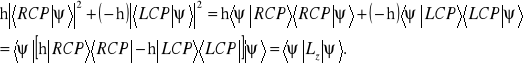
(8.9)

Pochłonięcie momentu pędu zachodzi niezależnie od rodzaju atomów, z których zbudowane są ścianki, towarzysząc pochłonięciu fotonu. Dlatego wyrażenie
traktować powinniśmy jako wielkość charakteryzującą foton, a nie materię. Powinniśmy uważać je za średnią wartość momentu pędu fotonu będącego w stanie
. Wielkość
nazywana jest także wartością oczekiwaną operatora
w stanie kwantowym
.

Teraz, dla zagadnienia badanego przez nas, możemy już sformułować następny postulat mechaniki kwantowej: Obserwowana zmiana momentu pędu materii spowodowana pochłonięciem jednego fotonu będącego w stanie polaryzacji
równa jest
- średniej wartości operatora momentu pędu fotonu
w stanie
. Oczywiście
możemy uważać za prawdopodobieństwo zachowania się fotonu będącego w stanie
tak jak foton w stanie
. To prawdopodobieństwo równe jest zero wtedy i tylko wtedy, gdy foton znajduje się w stanie ortogonalnym do
, tj.
.

8.3 Zasady obliczania prawdopodobieństw w mechanice kwantowej

Ustalimy teraz podstawowe zasady obliczania prawdopodobieństw obowiązujące w mecha­nice kwantowej. Dla przykładu rozpatrzymy prawdopodobieństwo przejścia fotonu będącego w stanie liniowej polaryzacji y, tj.
. Jak wiemy prawdopodobieństwo to znika bo
. Możemy jednak spróbować zastosować reguły rachunku prawdopodobieństwa obowiązujące w fizyce klasycznej. Z prawdopodobieństwem
foton może zachowywać się jak gdyby był w stanie
oraz z prawdopodobieństwem
- tak jak gdyby był w stanie
. Foton w stanie
może z prawdopodobieństwem
zachować się jak gdyby był w stanie x (czyli przechodzić przez analizator x), podobnie foton lewoskrętnie kołowo spolaryzowany z prawdopodobieństwem
może przejść przez analizator x. W wyniku zastosowania reguł znanych z fizyki klasycznej otrzymamy dla prawdopodobieństwa przejścia fotonu liniowo spolaryzowanego y przez analizator x wyrażenie, którego wartość nie znika

. (8.10)

Ponieważ otrzymany wynik sprzeczny jest z wynikami doświadczeń w przypadku układów mikroskopowych muszą obowiązywać inne reguły obliczania prawdopodobieństwa. Aby ustalić jaki są te reguły obliczymy amplitudę prawdopodobieństwa przejścia fotonu y przez analizator x

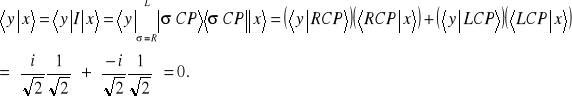
Jak widać gdy zastosujemy reguły klasycznego rachunku prawdopodobieństwa do amplitud to stwierdzimy, że amplituda
znika, zatem znika także prawdopodobieństwo
.

Zajmijmy się wyrażeniem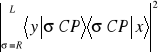
, mamy

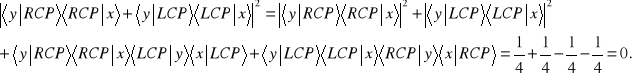
Jak widać stosując klasyczne reguły obliczania prawdopodobieństwa opuściliśmy dwa istotne wyrazy.

Nie staraliśmy się ustalić w jaki sposób foton y przechodzi przez analizator x. W ogóle nie dysponujemy informacją, która pozwoliłaby wyróżnić, któryś z tych dwóch sposobów. Możemy więc powiedzieć, że zdarzenie polegające na tym, że foton y może przejść przez analizator x na dwa nieodróżnialne sposoby - jako fonon prawoskrętnie kołowo spolaryzowany z amplitudą
albo jako prawostronnie kołowo spolaryzowany z amplitudą
. Będziemy mówili o dwóch nierozróżnialnych alternatywach realizacji zdarzenia w świecie mikroskopowym. W ten sposób udało się nam ustalić pierwszą regułę kwantowego rachunku prawdopodobieństwa: amplitudy prawdopodobień­stwa dwóch nierozróżnialnych realizacji zdarzenia dodajemy

.

Foton y może przejść przez analizator x z amplitudą prawdopodobieństwa
pod warunkiem, że zachowywał się jak gdyby był w stanie kołowym prawoskrętnie spolaryzowanym z amplitudą prawdopodobieństwa
. Postać amplitudy
mówi nam, że amplitudy prawdopodobieństw warunkowych należy mnożyć, np.

.

8.3 Uogólnienie zasad obliczania amplitud przejść i nowe postulaty

Uogólnimy otrzymane już wyniki i sformułujemy dodatkowe postulaty [3]. Zacznijmy od uogólnień.

1. Przyjmijmy, że przejście ze stanu i do stanu f może odbyć się na s nierozróżnialnych sposobów (Rys. 8.3). Amplituda przejścia jest równa sumie amplitud
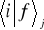
   odpowiadających różnym sposobom przejścia
   

(8.11a)

.

Rys. 8.2

2. Jeżeli przejście
   (
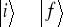
   ) odbywa się przez stan pośredni ν, o wektorze stanu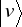
   , (Rys. 8.3) to amplituda prawdopodobieństwa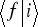
   jest równa iloczynowi amplitud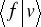
   ,
   

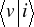
(8.11b)

Następne reguły sformułujemy w formie postulatów.

3. Załóżmy, że mamy do czynienia z dwoma obiektami mikroskopowymi. Niech pierwszy z nich ulega przejściu
   , a drugi
   (Rys. 8.4). Te przejścia charakteryzują amplitudy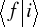
   ,
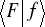
   . Amplituda przejścia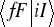
   złożonego układu ze stanu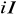
   do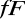
   równa jest iloczynowi amplitud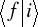
   ,
   

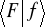
. (8.11c)

4. Przyjmijmy, że układ kwantowy może znaleźć się w jednym z
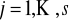
   rozróżnialnych stanów końcowych reprezentowanych przez wektory stanu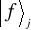
   (Rys. 8.5). Wyniki doświadczeń przeprowadzonych nad układem w stanach końcowych różnią się, to właśnie pozwala odróżnić te stany. Prawdopodobieństwo przejścia ze stanu i do któregoś ze stanów końcowych jest równe sumie prawdopodobieństw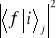
   

Rys. 8.5

. (8.11d)

W szczególnym przypadku gdy
,
wzór (8.11d) równoważny jest wzorowi (8.10) otrzymanemu w wyniku stosowania klasycznych reguł obliczania prawdopodobieństwa. Podstawowym postulatem jest rozróżnialność stanów cząstek, a więc zgodność wzorów (8.10) i (8.11d) nie jest przypadkowa.

8.4 Alternatywy rozróżnialne i nierozróżnialne

Za Baymem [2] zbadajmy co stanie się z prawdopodobieństwem, gdy będziemy starali się ustalić, która z możliwości przejścia fotonu przez polaryzator (R czy L) jest realizowana (Rys. 8.6). Niech polaryzację fotonu padającego na układ przedstawiony na Rys. 6 określa wektor stanu
. Stan początkowy fotonu można przedstawić w postaci superpozycji stanów
i
:
.

Rys. 8.6

Analizator A rozkłada
na
i
(zgodnie z R. 5 składa się on z kryształu dwójłomnego i półfalówki).
są zwierciadłami, które kierują wiązkę prawoskrętnie kołowo spolaryzowaną na układ B. Podobny układ zwierciadeł kieruje wiązkę lewostronnie kołowo spolaryzowaną na B. Układ B składa te dwie wiązki w jedną. X jest analizatorem x. Zwierciadła służą do ustalenia, którą drogę wybrał foton. W tym celu zmierzymy odrzut
i
wynikający z odbicia się fotonu. Zwierciadła
oraz
ustawione są tak by foton padał prawie prostopadle na
lub
. Pęd fotonu jest związany z wektorem falowym liczbą falową k oraz długością fali fotonu

.

Foton padając prostopadle na zwierciadło zmienia jego pęd o 2p. Aby móc określić którą z dróg wybrał foton, jego y-owa składowa powinna być określona z błędem

Lecz z zasady nieoznaczoności wynika, że

,

zatem błąd określenia współrzędnej wektora położenia Δy spełnia następujące nierówności

.

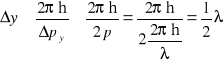
Ponieważ błąd pomiaru położenia zwierciadła M₂ względem zwierciadła M₁ przy pomocy fali wynosi
, podobnie błąd pomiaru położenia zwierciadła M₂ względem zwierciadła M₃ także jest równy
, więc całkowity błąd pomiaru odległości, którą przebędzie foton wynosi
. Stąd błąd pomiaru fazy jest równy

.

Jasne jest, że zupełnie nie umiemy ustalić fazy. Po odbiciu od zwierciadła
, którego pęd badamy, foton (początkowo liniowo spolaryzowany w kierunku y) może być w dowolnym stanie. Wykonany pomiar odrzutu zwierciadeł
tak zaburza stan fotonu, że nie umiemy określić w jakim stanie polaryzacji się on znajduje. Niech początkowo stan fotonu określa wektor stanu
. Musimy przyjąć, że stan końcowy
ma postać superpozycji z różnymi fazami
,

.

Przyjmijmy, że przeprowadziliśmy wiele takich doświadczeń. W każdym z doświadczeń faza fotonu przechodzącego przez analizator x może być inna, należy więc przeprowadzić odpowiednie uśrednienie. Amplituda prawdopodobieństwa przejścia fotonu w stanie początkowym
przez analizator x wynosi

.

Odpowiada jej prawdopodobieństwo

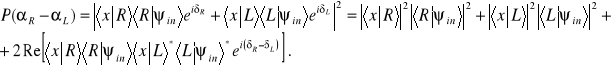
Ponieważ każde z doświadczeń jest niezależne, będziemy uśredniali prawdopodobieństwo w przedziale
. Nie trudno przewidzieć wynik uśredniania, Ponieważ

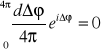
, (8.12)

to

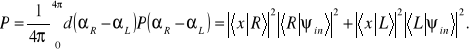
(8.13)

Jak widać gdy umiemy odróżnić stany końcowe układu mikroskopowego (w naszym przypadku stanu fotonu) to obowiązuje reguła nr 4 obliczania prawdopodobieństwa.

Jeżeli chcemy użyć zwierciadeł do ustalenia do ustalenia jaką drogę wybrał foton musimy ustalić położenie zwierciadeł z dokładnością

to musi być spełniona jest nierówność
, a więc nie możemy ustalić, które ze zwierciadeł uległo odrzutowi, a co za tym idzie rozróżnić stanu końcowego fotonu.

Gdy
, to po wykonaniu doświadczenia mającego za zadanie ustalić w jaki sposób foton
przeszedł przez
, stan fotonu jest tak zaburzony, że może być w każdym stanie a więc i w stanie x, czyli foton może przejść przez analizator x.

8.5 Zasada superpozycji w poezji

Zasada superpozycji zaprzątała nie tylko umysły uczonych ale także poetów. Przedstawia ją kwantowa „Ballada o słoniu” J. G. Saxe'a [4]. Ballada ta ilustruje także obecny stan dyskusji podstaw mechaniki kwantowej.

„Ballada o słoniu”

Żyło raz sześciu w Hindustanie

Ludzi ciekawych niesłychanie

I chociaż byli ślepi,

Wybrali kiedyś się na błonie

Aby zapoznać się ze słoniem

I umysł swój pokrzepić.

Pierwszy z nich przyśpieszywszy kroku

Nos rozbił na słoniowym boku

O twardą jego skórę;

Więc do swych towarzyszy pięciu

Krzyknął: - Już wiem o tym zwierzęciu

Że jest najtwardszym murem.

Gdy się do słonia zbliżył Drugi

Na kieł się natknął ostry, długi,

Więc swych przyjaciół ostrzegł:

- Ach uważajcie, moi mili,

Żebyście się nie skaleczyli,

Bo słoń to ostry oszczep!

Trzeci podchodząc do zwierzęcia,

Nie więcej miał od tamtych szczęścia:

Słoń trąbę swą rozprężał,

A on dotknąwszy trąby dłonią

Rzekł: - Ja już wszystko wiem o słoniu,

Słoń jest gatunkiem węża!

Wtedy powiedział ślepiec Czwarty,

Bardzo ciekawy i uparty:

- Chcę wiedzieć czego nie wiem! -

I kiedy sam przy słoniu stanął,

Rzekł obejmując mu kolano:

- Już wiem, że słoń jest drzewem!

Gdy się do słonia Piąty zbliżył,

Słoń siadł na ziemi, łeb obniżył

I ruszać jął uszami;

Więc Piąty, rzecz uogólniając,

Rzekł: - Już poznałem prawdę całą,

Słonie są wachlarzami!

Nie gorszy, choć ostatni Szósty,

Najpowolniejszy, bo był tłusty

I dał się innym minąć,

Rzekł, gdy za ogon słonia schwycił:

- Nie przypuszczałem nigdy w życiu,

Że słoń jest zwykłą liną!

I żaden z ślepców tych aż do dziś

Nie chce się z innym ślepcem zgodzić

Część prawdy tylko znając;

Każdy przy swojej trwa opinii,

Każdy ma rację swą, jak inni -

Lecz wspólnie jej nie mając.

Literatura

[1] G. Baym, Lectures on Quantum Mechanics, Benjamin, Reading Mass., 1974, R. 1.

[2] R. P. Feynman, R.B. Leighton, M. Sands, Feynmana wykłady z fizyki, PWN, Warszawa, 1972, § 17.4.

[3] L. W. Tarasow, Podstawy mechaniki kwantowej, PWN Warszawa, 1992.

[4] Edward Lear i inni, “Księga nonsensu” napisane po polsku przez Antoniego Marianowi­cza i Andrzeja Nowickiego, Wydawnictwa Artystyczne i Filmowe, Warszawa, 1975

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---