KONDUKTOMETRIA - RUCH JONÓW W ROZTWORZE

Przewodniki dzielimy na :

• elektronowe

• jonowe

W przewodnikach elektronowych nośnikiem prądu są elektrony (czasem też dziury). Przepływowi ładunku elektrycznego nie towarzyszy ruch masy, ani żadne reakcje chemiczne. Przewodnictwo ich maleje ze wzrostem temperatury. Należą tu metale i półprzewodniki.

W przewodnikach jonowych nośnikiem prądu są jony. Przepływowi ładunku towarzyszy ruch masy i mogą zachodzić reakcje chemiczne. Przewodnictwo ich rośnie wraz ze wzrostem temperatury. Należą tu kryształy o budowie jonowej, stopione sole, zjonizowane gazy i roztwory elektrolitów.

W tym dziale będziemy się zajmować przewodzeniem prądu przez roztwory elektrolitów. Gdy przez roztwór elektrolitu płynie prąd stały, jony wędrują do odpowiednich elektrod, gdzie ulegają rozładowaniu, wydzielają się rozmaite substancje. Zjawisko to nosi nazwę elektrolizy. Konkretne reakcje na elektrodach zależą od wielu czynników jak : przyłożone napięcie, gęstość prądu, skład roztworu, pH, materiał, z którego zbudowane są elektrody. W szczegóły nie będziemy wchodzić, bo nie tu na to miejsce.

Rysunek 1. Elektroliza.

Elektrolizą rządzą dwa prawa sformułowane przez Michała Faraday'a.

I prawo Faraday'a

Kiedy przez roztwór przepływa prąd stały, to ładunek można wyrazić jako iloczyn czasu trwania elektrolizy i natężenia prądu. Wówczas :

II prawo Faraday'a

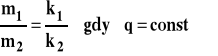
Elektroliza jest zjawiskiem o bardzo dużym znaczeniu praktycznym. Jest podstawą wielu elektrochemicznych metod analizy jak analiza elektrograwimetryczna, miareczkowanie kulometryczne, amperometryczne, amperometria i wiele innych. Ponadto elektroliza jest podstawą wielu procesów w metalurgii jak otrzymywanie glinu, rafinacja miedzi i wydzielanie srebra i złota ze szlamów porafinacyjnych. Elektrolitycznie nanosi się powłoki galwaniczne z metali bardziej szlachetnych na mniej szlachetnych, na przykład chromowanie czy niklowanie stali, platerowanie mosiądzu.

Przewodzenie prądu przez dowolny przewodnik jest opisane prawami Ohma znanymi z kursu fizyki. Dla przypomnienia :

I prawo Ohma

Współczynnik proporcjonalności w tym wzorze to opór. Jednostką oporu jest om (

II prawo Ohma

gdzie : ρ - oporność (dawniej - opór właściwy) l - długość przewodnika A - pole przekroju poprzecznego, prostopadłego do kierunku przepływu prądu

Współczynnik proporcjonalności w tym wzorze nazywamy opornością (obecnie obowiązująca nazwa). Oporność to opór przewodnika o długości jednostkowej i jednostkowym polu przekroju poprzecznego do kierunku przepływu prądu. Jednostką jest m.

Przewodnictwo to odwrotność oporu. Jednostką jest simens (S).

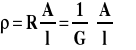
Przewodność to odwrotność oporności. Jednostką jest Sm^-1. Oznaczamy ją grecką literą  (kappa). Dawniej nazywano tę wielkość przewodnictwem właściwym, obecnie obowiązuje nazwa przewodność.

Przewodność jest podstawową wielkością przy opisie przewodzenia prądu przez roztwory elektrolitów, musimy ją więc dokładnie zdefiniować.

Przewodność elektrolityczna

Interpretacja przewodności elektrolitycznej pokazana jest na rysunku 2.

Rysunek 2. Interpretacja przewodności elektrolitycznej.

Jako przewodność elektrolityczną rozumiemy przewodnictwo sześcianu o boku jednostkowym, zawierającego roztwór elektrolitu, umieszczonego w jednorodnym polu elektrycznym.

Do pomiaru przewodności elektrolitycznej służy zmodyfikowany mostek Wheatstone'a pokazany na rysunku 3.

Rysunek 3. Mostek Wheatstone'a używany do pomiarów przewodności elektrolitycznej.

Mostek ten jest zasilany prądem zmiennym (zwykle o częstotliwości 1 kHz), aby :

• zapobiec polaryzacji elektrod

• zapobiec elektrolizie roztworu

W trakcie pomiarów naczynko konduktometryczne musi być termostatowane (najlepiej z dokładnością do 0,1 stopnia), ponieważ przewodnictwo roztworów rośnie silnie wraz ze wzrostem temperatury. Ponieważ w zmiennym polu elektrycznym naczynko konduktometryczne wykazuje pozorny opór pojemnościowy, to w obwód włączony jest kondensator o zmiennej pojemności, kompensujący pojemność elektryczną naczynka.

W zasadzie przy użyciu mostka mierzymy opór naczynka konduktometrycznego napełnionego roztworem elektrolitu. Pomiar sprowadza się do takiego dobrania oporów R₁, R₂ i R₃ (oraz pojemności C₂), aby pomiędzy punktami A i B w obwodzie nie płynął prąd. Wówczas galwanometr włączany w obwód pokaże zero. Jeśli pomiędzy punktami A i B nie płynie prąd, to potencjały elektryczne w obu tych punktach są jednakowe.

W punktach C i D prąd płynący w dolnej części obwodu jest podzielony. Ponieważ pomiędzy punktami A i B nie ma przepływu prądu, gdy mostek jest w równowadze, to natężenie prądu płynącego przez oporniki R₁ i R₃ jest takie samo oraz płynącego przez opornik R₂ i naczynko R_x taki sam.

Ponieważ potencjały w punktach A i B są takie same, to spadki napięcia na odcinkach DB i DA są takie same oraz na odcinkach BC i AC także.

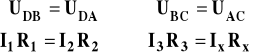
Po podzieleniu stronami otrzymujemy :

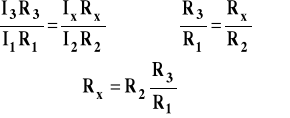
Teoretycznie rzecz biorąc, gdybyśmy znali odległość pomiędzy elektrodami oraz powierzchnie elektrod, pod warunkiem, że byłyby one równoległe do siebie i pole elektryczne pomiędzy nimi byłoby jednorodne, to przewodność elektrolityczną można by obliczyć ze wzoru :

W typowych naczynkach konduktometrycznych praktycznie żaden z tych warunków nie jest spełniony. Ani elektrody nie są równoległe, ani pole elektryczne pomiędzy nimi nie jest jednorodne. Ponadto zwykle nie znamy parametrów geometrycznych czyli odległości pomiędzy elektrodami ani ich powierzchni. Jak więc dokonujemy pomiaru przewodności ? Zakładamy, że wdanym naczynku przewodność jest proporcjonalna do przewodnictwa i oznaczamy współczynnik proporcjonalności, pod którym kryją się parametry geometryczne układu, jako k czyli stałą naczynka.

Następnie mierzymy opór naczynka wypełnionego roztworem wzorcowym o znanej przewodności elektrolitycznej i obliczamy stałą naczynka :

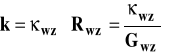
Następnie mierzymy opór naczynka wypełnionego roztworem badanym i znając już stałą naczynka obliczamy przewodność elektrolityczną.

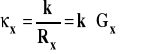
Pomiar przewodności elektrolitycznej jest więc pomiarem porównawczym. Przy użyciu mostka Wheatstone'a porównujemy przewodności wzorca i badanego roztworu elektrolitu. Jako wzorzec używa się roztworów chlorku potasowego. Przewodności elektrolityczne wzorcowych roztworów KCl podane są tabeli poniżej.

Przewodność elektrolityczna wzorcowych roztworów KCl

stężenie [mol/dm^3]	 w 18ºC [Sm^-1]	 w 25ºC [Sm^-1]
1	9,820	11,173
0,1	1,1192	1,2886
0,01	0,12227	0,14115

W praktyce laboratoryjnej używa się obecnie automatycznego mostka Wheatstone'a, który mierzy wprost przewodnictwo, zwanego konduktometrem.

Przewodność elektrolityczna roztworów elektrolitów zależy od stężenia. Oczywistym jest, że im wyższe stężenie tym więcej jest nośników prądu (jonów) i przewodność powinna rosnąć. Na pierwszy rzut oka wydaje się, że przewodność elektrolityczna powinna być wprost proporcjonalna do stężenia elektrolitu. I tak w przybliżeniu jest dla rozcieńczonych roztworów mocnych elektrolitów (rysunek 4).

Rysunek 4. Przykłady zależności przewodności elektrolitycznej od stężenia dla kilku różnych elektrolitów.

Jednakże przy wyższych stężeniach zależność przewodności od stężenia staje się nieliniowa. Zwykle zależność taka przechodzi przez maksimum, a dla bardzo dużych stężeń przewodność zaczyna maleć wraz ze wzrostem stężenia. Przyczyną takiej zależności są oddziaływania pomiędzy jonami prowadzące do powstawania atmosfery jonowej, a przy wysokich stężeniach asocjacja jonów. Dla słabych elektrolitów (kwas octowy na rysunku 4) przewodności elektrolityczne są znacznie mniejsze niż dla mocnych. Zauważmy, że wartości dla kwasu octowego na rysunku zostały pomnożone przez 10, aby w ogóle było coś widać. Ponadto przewodność w żadnym obszarze stężeń nie jest proporcjonalna do stężenia.

Fakt, że w obszarze niskich stężeń przewodność elektrolityczna jest wprost proporcjonalna do stężenia, nasunął pomysł, aby przeliczyć przewodność na 1 mol elektrolitu. W ten sposób powstało pojęcie przewodności molowej.

Przewodność molowa

Przewodność molowa oznaczana jest  (duża lambda). Jednostką jest ^-1m²mol^-1 lub Sm²mol^-1. Przewodność molowa obliczamy ze wzoru :

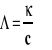
Należy przy tym pamiętać, aby wartość stężenia podstawiać w tym wzorze wyrażoną w mol/m³. Interpretacja przewodności molowej pokazana jest na rysunku 5.

Rysunek 5. Interpretacja przewodności molowej.

Jako przewodność molową rozumiemy przewodnictwo prostopadłościanu zawierającego roztwór elektrolitu, o jednostkowej grubości i takiej objętości, że znajduje się w niej 1 mol elektrolitu, umieszczonego w jednorodnym polu elektrycznym.

Aby móc porównywać przewodnictwo roztworów elektrolitów zawierających jony o różnej wartościowości np. KCl, MgCl₂ i FeCl₃, wprowadzono pojecie przewodności równoważnikowej czyli przypadającej na jeden mol ładunku elementarnego.

Przewodność równoważnikowa

Przewodność równoważnikową oznaczamy jako _eqv. Pomiędzy przewodnością molową a równoważnikową zachodzi związek :

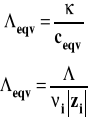
Przewodność molowa i równoważnikowa zależą od stężenia elektrolitów. Maleją wraz ze wzrostem stężenia elektrolitu, przy czym dla mocnych elektrolitów nieznacznie, a dla słabych bardzo silnie.

Dla mocnych elektrolitów zależność przewodności molowej od stężenia może być opisana wzorem Kohlrauscha, sformułowanym na podstawie wyników eksperymentalnych.

Wzór Kohlrauscha

Dla mocnych elektrolitów przewodność molowa maleje liniowo wraz ze wzrostem pierwiastka ze stężenia elektrolitu. Stała b w tym wzorze zależy od układu elektrolit-rozpuszczalnik oraz od temperatury. _o to graniczna przewodność molowa.

Graniczna przewodność molowa (równoważnikowa)

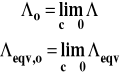
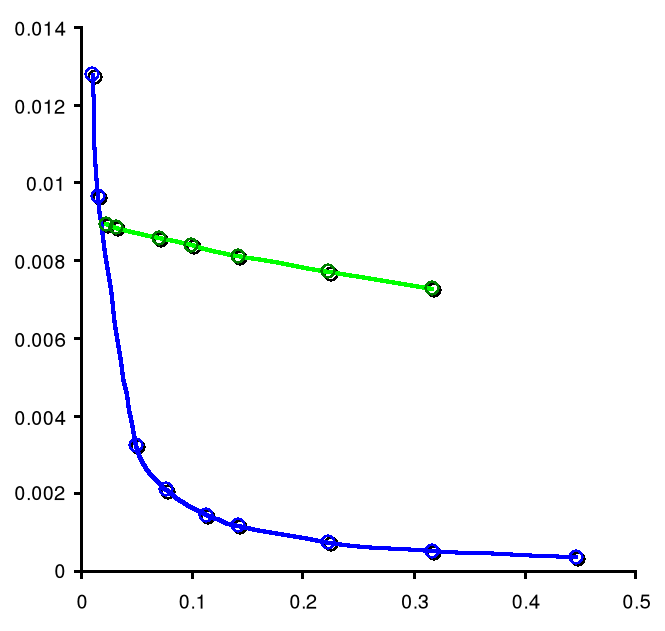
Wzór Kohlrauscha jest dobrze spełniany dla stężeń nieprzekraczających 0,01 mol/dm³. Dla wyższych stężeń pojawiają się odchylenia (rysunek 6) spowodowane istnieniem atmosfery jonowej wokół jonów. Wzór Kohlrauscha ma uzasadnienie teoretyczne w oparciu o teorię roztworów mocnych elektrolitów. Korzystając z tego wzoru można przez ekstrapolację do zerowego stężenia wyznaczyć graniczną przewodność molową dla mocnych elektrolitów (rysunek 6). Wobec tego, aby znaleźć doświadczalnie _o, trzeba zrobić serię roztworów o różnych stężeniach, ale nieprzekraczających 0,01 mol/dm³. Następnie należy zmierzyć dla nich przewodności elektrolityczne, obliczyć przewodności molowe i zbudować wykres zależności przewodności molowej od pierwiastka ze stężenia elektrolitu.

Rysunek 6. Przykładowe zależności przewodności molowej od pierwiastka ze stężenia elektrolitu.

Na rysunku 6 pokazano taką zależność dla mocnego elektrolitu (octanu sodowego) i sposób ekstrapolacji do stężenia zerowego. Dla porównania pokazano zależność przewodności molowej od pierwiastka ze stężenia dla słabego elektrolitu (kwasu octowego). Jak widać w całym zakresie jest to zależność nieliniowa i dla słabego elektrolitu nie można wyznaczyć granicznej przewodności molowej przez ekstrapolację do stężenia zerowego. Powstaje więc pytanie, jak znaleźć tę wielkość dla słabego elektrolitu ? Pomocne jest tu prawo niezależnej wędrówki jonów Kohlrauscha. Jak wiadomo, w roztworze elektrolitu nośnikami ładunku są jony (kationy i aniony) i ich przewodności składają się na przewodność całego roztworu.

Prawo niezależnej wędrówki jonów Kohlrauscha

Na mocy tego prawa przewodność molową elektrolitu można przedstawić jako sumę przewodności molowych poszczególnych jonów (oznaczane  - mała lambda), na jakie dysocjuje elektrolit, pomnożone przez ich liczbę.

Wprowadzając przewodność równoważnikową jonu

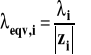
można przewodność równoważnikową elektrolitu przedstawić jako sumę przewodności równoważnikowych kationu i anionu.

Przewodność elektrolityczną można wyrazić jako sumę iloczynów stężeń poszczególnych jonów w roztworze i ich przewodności molowych, przy czym sumowanie należy wykonać po wszystkich jonach występujących w roztworze.

Jak więc w oparciu o to prawo można znaleźć graniczne przewodnictwo molowe słabego elektrolitu, niemożliwe do wyznaczenia w sposób doświadczalny ? Odpowiedź na to pytanie pokażemy na przykładzie.

PRZYKŁAD

Wyznaczyć graniczną przewodność molową kwasu propionowego (słaby elektrolit) znając graniczne przewodności molowe propionianu sodowego, chlorku sodowego i kwasu solnego.

Rozwiązanie

Graniczne przewodności molowe propionianu sodowego, chlorku sodowego i kwasu solnego można wyznaczyć doświadczalnie, gdyż są to mocne elektrolity. Przedstawmy przewodności molowe każdej z tych substancji przez przewodności jonów.

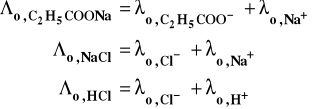
Podobnie możemy przedstawić przewodność molową kwasu propionowego.

Łatwo zauważyć, że pomiędzy nimi zachodzi związek :

gdyż :

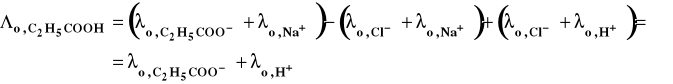
Teraz zostaje podstawienie tylko odpowiednich danych uzyskanych w wyniku eksperymentu.

Graniczne przewodności molowe (równoważnikowe) dla wielu jonów są znane. Przykładowe wartości dla kilkunastu wybranych kationów i anionów w roztworze wodnym pokazane są w tabeli poniżej.

Przykładowe wartości granicznych przewodności równoważnikowych jonów w temperaturze 25*C w roztworach wodnych [^-1m²mol^-1]

kationy		Aniony
H^+	349,65·10^-4	OH^-	198·10^-4
Na^+	50,08·10^-4	Cl^-	76,31·10^-4
K^+	73,48·10^-4	Br^-	78,1·10^-4
NH4^+	73,5·10^-4	J^-	76,8·10^-4
Li^+	38,66·10^-4	NO3^-	71,42·10^-4
1/2 Mg^2+	53,0·10^-4	CH3COO^-	40,9·10^-4
1/2 Ca^2+	59,47·10^-4	1/2 SO4^2-	80,0·10^-4
1/2 Ba^2+	63,6·10^-4	1/2 CO3^2-	69,3·10^-4
1/3 Al^3+	61·10^-4	1/3 Fe(CN)6^3-	100,9·10^-4
1/3 Fe^3+	68·10^-4	C10H21SO4^-	26·10^-4

Co można zauważyć przyglądając się danym w tej tabeli ? Przewodności równoważnikowe większości jonów są bardzo zbliżone. Wyjątkiem jest duży organiczny anion, dla którego przewodność jest zdecydowanie mniejsza oraz jony H⁺ i OH^-, pochodzące z autodysocjacji wody, które wyróżniają się wyjątkowo dużą przewodnością. Aby wyjaśnić te spostrzeżenia, musimy się nieco bliżej przyjrzeć ruchowi jonów w roztworze pod wpływem pola elektrycznego. Pozostaje jeszcze jedno zasadnicze pytanie. Jak znaleziono przewodności równoważnikowe jonów, skoro, jak to wielokrotnie podkreślano, nie można zrobić roztworu jednego rodzaju jonów ? Na to pytanie odpowiemy sobie nieco później.

Ruch jonu w roztworze pod wpływem pola elektrycznego

Kiedy jon porusza się w roztworze, działają na niego dwie siły : siła elektryczna wprawiająca go w ruch i siła oporu lepkiego (rysunek 7).

Rysunek 7. Siły działające na jon poruszający się w roztworze pod wpływem pola elektrycznego.

Siła elektryczna wyraża się wzorem :

Siła oporu lepkiego przy założeniu, że jon jest kulisty, opisana jest wzorem Stokesa :

gdzie : E - natężenie pola elektrycznego e - ładunek elementarny  - lepkość rozpuszczalnika r_i - promień hydrodynamiczny jonu v_i - szybkość poruszania się jonu

Jeśli szybkość poruszania się jonu jest stała, to siły te są w równowadze.

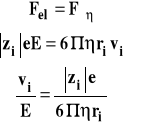
Stosunek szybkości poruszania się jonu do natężenia pola elektrycznego nazywamy ruchliwością jonu.

Ruchliwość jonu

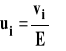
Jednostką ruchliwości jest m²/Vs. Ruchliwość jonu zależy od jego promienia hydrodynamicznego (pamiętamy, że w wodzie jon porusza się z pierwotną warstwą hydratacyjną), lepkości środowiska oraz ładunku. Pośrednio ruchliwość jonu zależy także od temperatury, gdyż lepkość cieczy maleje wraz ze wzrostem temperatury. Skoro tak, to ruchliwość rośnie wraz ze wzrostem temperatury.

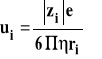
Ruchliwość można powiązać z przewodnością równoważnikową jonu następującym związkiem.

gdzie : F - stała Faraday'a; F = 96500 C/mol

Wobec tego jasnym staje się, dlaczego przewodnictwo roztworów elektrolitów rośnie wraz ze wzrostem temperatury. Skoro ruchliwość rośnie, to przewodność równoważnikowa, która jest do niej wprost proporcjonalna, też rośnie.

Mechanizm przewodzenia jonów H⁺ i OH^- w wodzie

Jak zauważyliśmy, analizując tabelę wartości przewodności równoważnikowych różnych jonów w wodzie, wartości przewodności są porównywalnej wielkości. Jest to zrozumiałe w świetle czynników wpływających na ruchliwość jonu. Promienie hydrodynamiczne jonów są zbliżone do siebie, a więc i ich ruchliwości i przewodności są też podobne. Natomiast przewodności jonów pochodzących z autodysocjacji wody są znacznie większe.

Jeśli weźmiemy pod uwagę jon H⁺, to wiemy że tak naprawdę w wodzie istnieje on jako H₃O⁺. Promień jego jest porównywalny z promieniami innych jonów. Powinien wobec tego mieć przewodność porównywalną z innymi jonami. A tak nie jest. Wskazuje to, że mechanizm przewodzenia dla tych jonów jest inny.

Jon H₃O⁺ stale wymienia proton z sąsiednimi cząsteczkami wody. W efekcie jego położenie ciągle się zmienia.

Rysunek 8. Wymiana protonu pomiędzy jonem hydroniowym a cząsteczkami wody.

W nieobecności pola elektrycznego oba położenia ładunku dodatniego pokazane na rysunku 8 są jednakowo prawdopodobne. W obecności pola elektrycznego proton o ładunku dodatnim będzie przeskakiwał w kierunku ujemnej elektrody. W ten sposób ładunek dodatni będzie wędrował poprzez kolejne przeskoki pomiędzy sąsiednimi cząsteczkami wody. Jest to tak zwany mechanizm łańcuchowy (rysunek 9).

Rysunek 9. Mechanizm łańcuchowy wędrówki jonów H₃O⁺ w wodzie w polu elektrycznym.

Podobnie wygląda mechanizm wędrówki jonów OH^- w wodzie, przy czym w tym wypadku kierunek wędrówki jonu jest przeciwny do kierunku przeskoku protonu (rysunek 10).

Rysunek 10. Mechanizm łańcuchowy wędrówki jonów OH^- w wodzie w polu elektrycznym.

Liczby przenoszenia jonów

Kiedy przez roztwór elektrolitu przepływa prąd elektryczny, to nośnikami ładunku są jony. Wobec tego, część ładunku przenoszonego przez roztwór transportowana jest przez kationy, część przez aniony. Jaki ułamek całkowitego ładunku jest przenoszony przez jony danego znaku określają liczby przenoszenia jonów.

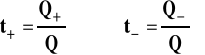
Liczby przenoszenia kationu i anionu w danym elektrolicie sumują się zawsze do jedności.

Można wykazać, że liczby przenoszenia jonów są powiązane z przewodnościami równoważnikowymi lub molowym jonów następującymi zależnościami.

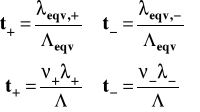
Liczby przenoszenia jonów można wyznaczać doświadczalnie. Istnieją dwie metody ich wyznaczania :

• metoda Hittorfa

• metoda ruchomej granicy

Metod tych nie będziemy tu omawiać, z jedną z nich (Hittorfa) zapoznają się Państwo na laboratorium z chemii fizycznej.

Po co wyznacza się liczby przenoszenia jonów ? Niezbędne są one do wyznaczenia przewodnictw równoważnikowych i molowych jonów. Aby tego dokonać, trzeba zrobić dwa niezależne doświadczenia. W pierwszym mierzymy przewodność elektrolityczną badanego elektrolitu i obliczamy przewodność molową bądź równoważnikową. W drugim eksperymencie wyznaczamy liczby przenoszenia jonów w tym elektrolicie. Przekształcając wzory podane powyżej, otrzymujemy :

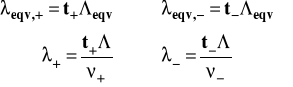
Wykorzystanie pomiarów konduktometrycznych

Pomiary przewodności roztworów można wykorzystać między innymi do :

• Wyznaczania iloczynu rozpuszczalności soli trudno rozpuszczalnych

• Wyznaczania iloczynu jonowego wody

• Wyznaczania stałych dysocjacji słabych elektrolitów

• Miareczkowania konduktometryczne

Sposoby znajdowania iloczynu rozpuszczalności i stałych dysocjacji są omawiane szczegółowo na ćwiczeniach rachunkowych, a także praktycznie ćwiczone na zajęciach laboratoryjnych. Niemniej jednak powtórzymy tu je w skrócie. Ponadto pomiar przewodnictwa, a dokładniej wartość przewodności elektrolitycznej jest bardzo dobrą miarą czystości wody i jej zasolenia.

Wyznaczanie iloczynu rozpuszczalności soli trudno rozpuszczalnej

Rozpuszczanie się soli trudno rozpuszczalnej w wodzie formalnie można opisać równa-niem :

Iloczyn rozpuszczalności wyraża się wzorem :

Dla roztworów bardzo rozcieńczonych, a takimi są roztwory nasycone soli trudno rozpuszczalnych, aktywność jest w przybliżeniu równa stężeniu.

Iloczyn rozpuszczalności można wobec tego wyrazić jako :

Jeżeli oznaczymy stężenie roztworu nasyconego soli (rozpuszczalność) jako s, to stężenia anionów i kationów można wyrazić jako :

a iloczyn rozpuszczalności :

Celem pomiaru przewodnictwa jest wyznaczenie stężenia roztworu nasyconego soli trudno rozpuszczalnej. W tym celu mierzymy przewodność elektrolityczną roztworu nasyconego i wody, z której sporządzono roztwór. Dlaczego tak robimy ? W wodzie nawet bardzo czystej mamy jony pochodzące z autodysocjacji wody. Ponadto w wodzie rozpuszcza się dwutlenek węgla z powietrza, który reaguje według równania :

Ponadto w wodzie mogą być rozmaite dodatkowe zanieczyszczenia, na przykład jony Na⁺ wymywane z ścian szklanych naczyń. W efekcie woda wykazuje pewne przewodnictwo. Na przewodnictwo roztworu nasyconego zgodnie z prawem niezależnej wędrówki jonów Kohlrauscha składają się udziały pochodzące od wszystkich jonów w roztworze :

Czyli przewodność roztworu nasyconego to suma przewodności pochodzącej od samej soli i od wszystkich jonów zawartych w samej wodzie.

Wobec tego przewodność pochodząca od samej soli to :

Skorzystamy ze wzoru na obliczanie przewodności molowej :

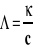
Jeśli do wzoru tego podstawimy przewodność soli, to uzyskamy stężenie roztworu nasyconego. Ponieważ roztwór jest bardzo rozcieńczony, przewodność molowa jest praktycznie równa granicznej przewodności molowej, którą obliczamy korzystając z danych w tablicach i zależności omówionych wcześniej :

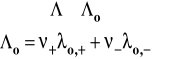
Ostatecznie stężenie roztworu nasyconego obliczymy ze wzoru :

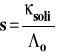
Przy obliczeniach należy zwracać uwagę na jednostki, gdyż z ostatniego wzoru otrzymujemy stężenie wyrażone w mol/m³, a do wzoru na iloczyn rozpuszczalności podstawiamy wartość wyrażoną w mol/dm³, tylko bez miana.

W podobny sposób wyznacza się iloczyn jonowy wody, mierząc przewodność elektrolityczną wody. Do pomiarów należy dysponować absolutnie czystą wodą, destylowaną w aparaturze kwarcowej lub platynowej, przechowywaną bez dostępu powietrza. Sam pomiar musi też być wykonywany w warunkach bez dostępu powietrza.

Wyznaczanie stałych dysocjacji słabych elektrolitów

Omówimy to wyznaczanie na przykładzie słabego kwasu HA, który dysocjuje częściowo według równania :

Stałą dysocjacji tego kwasu można wyrazić jako :

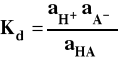
Dla roztworów rozcieńczonych można przyjąć, że aktywności równe są stężeniom :

i stałą dysocjacji zapisać jako :

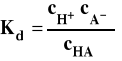
Jeśli stężenie kwasu wynosi c, a jego stopień dysocjacji , to stężenia jonów i niezdysocjowanego kwasu wynoszą :

Wyrażenie na stałą dysocjacji przybiera więc postać :

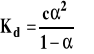
Wzór ten nosi nazwę prawa rozcieńczeń Ostwalda. Aby wyznaczyć stałą dysocjacji, trzeba znać stopień dysocjacji przy danym stężeniu. W tym celu mierzymy przewodność elektrolityczną roztworu o znanym stężeniu, a następnie obliczamy przewodność molową kwasu. Przewodność molowa kwasu o skończonym stężeniu może być wyrażona następująco :

Jeśli założymy, że przewodności molowe jonów nie zależą od stężenia i są w przybliżeniu równe granicznym, a tak można zrobić dla roztworów rozcieńczonych, otrzymamy, że :

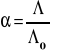
Potrzebną do obliczenia stopnia dysocjacji wielkość _o znajdujemy z tablic. Czasem prawo rozcieńczeń Ostwalda przekształcane jest do postaci, w której mamy wprost przewodności molowe.

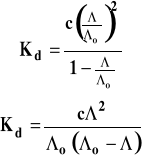
Miareczkowanie konduktometryczne

Celem każdego miareczkowania jest wyznaczenie punktu równoważnikowego miareczkowania, aby następnie na podstawie ilości zużytego titranta (odczynnika miareczkowego) obliczyć ilość oznaczanej substancji. Ze względu na rodzaj reakcji używanej w miareczkowaniu wyróżniamy :

• Miareczkowania kwasowo-zasadowe

• Miareczkowania strąceniowe

• Miareczkowania redoksymetryczne

• Miareczkowania kompleksometryczne

Dotychczas podczas kursu chemii analitycznej punkt równoważnikowy miareczkowania obserwowany był przez zmianę barwy wskaźnika. Metoda taka zawodzi, gdy sama próbka jest barwna lub nieprzezroczysta. Wyobraźmy sobie, że chcemy oznaczyć ilość kwasów w próbce soku wiśniowego stosując jako wskaźnik fenoloftaleinę. Będzie to oczywiście praktycznie niemożliwe. Aby unikać takich problemów, stosuje się rozmaite metody instrumentalne, w których mierzymy zmiany jakiejś wielkości fizycznej powiązanej ze stężeniem reagentów w czasie miareczkowania. Jednym z takich typów miareczkowania jest miareczkowanie konduktometryczne.

Miareczkowanie konduktometryczne polega na wyznaczaniu punktu równoważnikowego pośrednio poprzez pomiar przewodnictwa. W tym celu do próbki dodajemy porcjami roztwór titranta i po każdym dodaniu mierzymy przewodnictwo roztworu. Podstawą metody jest prawo niezależnej wędrówki jonów Kohlrauscha.

Przewodność roztworu jest sumą przewodności pochodzących od wszystkich jonów w nim obecnych. W trakcie miareczkowania na skutek zachodzącej reakcji zmieniają się zarówno stężenia, jak i rodzaj jonów w roztworze, wobec tego przewodnictwo roztworu zmienia się. Metodę miareczkowania konduktometrycznego można wykorzystać do miareczkowań kwasowo-zasadowych, strąceniowych i kompleksometrycznych.

Poniżej zostaną przedstawione dwa przykłady miareczkowania konduktometrycznego, kwasowo-zasadowego.

Miareczkowanie mocnej zasady mocnym kwasem

Krzywa miareczkowania pokazana jest na rysunku 11.

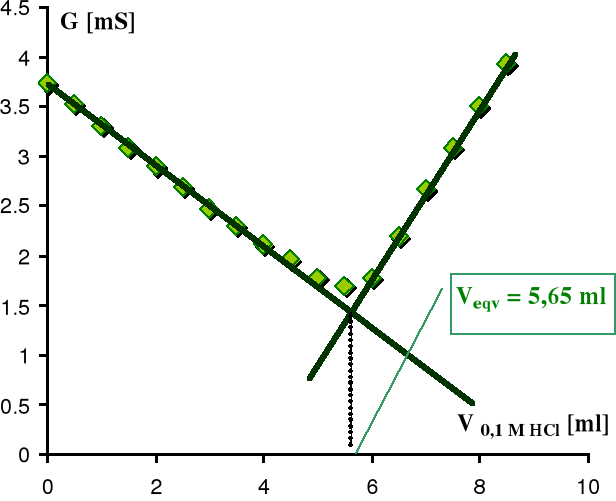
Rysunek 11. Miareczkowanie roztworu NaOH roztworem mianowanym HCl.

W trakcie tego miareczkowania zachodzi reakcja :

Jony OH^- o dużej ruchliwości i przewodności są wiązane przez jony H⁺ do cząsteczek wody, a na ich miejsce pojawiają się jony Na⁺ o znacznie mniejszej przewodności. Wobec tego przewodność maleje. Po przekroczeniu punktu równoważnikowego, gdy praktycznie wszystkie jony OH^- są już związane, dalsze dodawanie roztworu HCl prowadzi do szybkiego wzrostu przewodnictwa, gdyż dodajemy jony H⁺ o bardzo dużej ruchliwości i przewodności. Punkt równoważnikowy znajduje się jako punkt przecięcia prostych przechodzących przez dwie gałęzie krzywej miareczkowania, jak to pokazano na rysunku 11.

Miareczkowanie słabego kwasu mocną zasadą

W tym wypadku na lewej gałęzi krzywej miareczkowania pojawia się minimum związane z hydrolizą powstającej soli słabego kwasu i mocnej zasady.

Po przekroczeniu tego minimum przewodnictwo rośnie liniowo. Po przekroczeniu punktu równoważnikowego zaczyna ono rosnąć bardzo szybko, gdyż dodawane jony OH^- już nie są wiązane przez kwas, który został całkowicie zobojętniony. Krzywa miareczkowania i sposób wyznaczania punktu równoważnikowego zostały pokazane na rysunku 12.

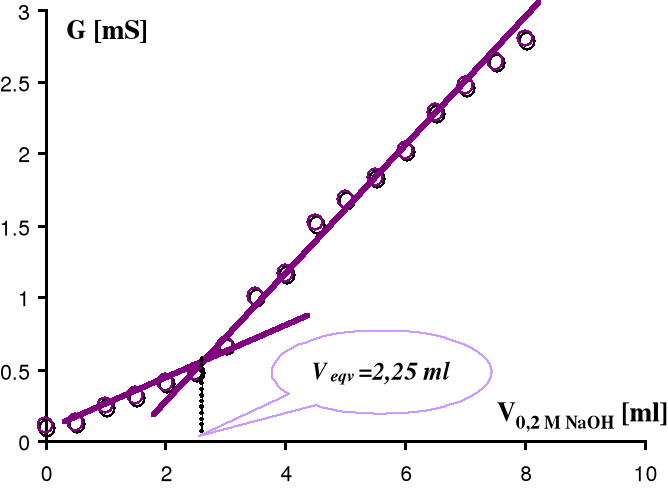
Rysunek 12. Miareczkowanie roztworu CH₃COOH mianowanym roztworem NaOH.

Miareczkowanie konduktometryczne pozwala na dokładne miareczkowanie nawet rozcieńczonych roztworów słabych kwasów. Ponadto pozwala na miareczkowanie obok siebie w jednej próbce słabego i mocnego kwasu lub słabej i mocnej zasady. W bardzo dokładnych oznaczeniach w opracowaniu wyników uwzględnia się poprawki na rozcieńczanie próbki.

katoda anoda

A^-

K⁺

+

_

e

Masa substancji wydzielonej na elektrodzie jest wprost proporcjonalna do ładunku, jaki przepłynął przez roztwór.

Jeżeli przez roztwory przepłynął ten sam ładunek, to masy dwu substancji wydzielonych na elektrodach mają się do siebie jak ich współczynniki elektrochemiczne.

Natężenie prądu płynącego przez opornik jest wprost proporcjonalne do napięcia.

Opór opornika jest wprost proporcjonalny do jego długości, a odwrotnie proporcjonalny do jego pola przekroju poprzecznego do kierunku prądu.

Przewodność elektrolityczna (dawniej - przewodnictwo właściwe elektrolitu) jest to przewodnictwo roztworu elektrolitu zawartego pomiędzy równoległymi elektrodami odległymi o jednostkę (1 m) i polu przekroju poprzecznego słupa cieczy zawartego między nimi jednostkowym (1 m²), przy czym pole elektryczne pomiędzy elektrodami jest jednorodne.

kierunek przepływu prądu

1 m²

1 metr

G

C_x

R₁

R₂

R₃

R_x

C₂

B

C

D

A

galwanometr

kondensator o zmiennej pojemności

prąd zmienny o częstotliwości 1000 Hz

~

naczynko konduktometryczne

przewodność elektrolityczna [Sm^-1]

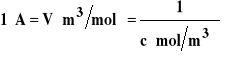
kierunek przepływu prądu

c [mol/dm³]

12

10

8

6

4

2

0

160

140

120

100

80

60

40

20

0

CH₃COOH x10

HJ

NaOH

H₂SO₄

Przewodność molowa (dawniej - przewodnictwo molowe) jest to przewodnictwo roztworu elektrolitu zawartego pomiędzy równoległymi elektrodami odległymi o jednostkę (1 m) i o takim polu przekroju poprzecznego słupa cieczy zawartego między nimi, że w tak utworzonej objętości zawarty jest jeden mol elektrolitu, przy czym pole elektryczne pomiędzy elektrodami jest jednorodne.

A

1 metr

Przewodność równoważnikowa (dawniej - przewodnictwo równoważnikowe) jest to przewodnictwo roztworu elektrolitu zawartego pomiędzy równoległymi elektrodami odległymi o jednostkę (1 m) i o takim polu przekroju poprzecznego słupa cieczy zawartego między nimi, że w tak utworzonej objętości zawarty jest jeden gramorównoważnik elektrolitu, przy czym pole elektryczne pomiędzy elektrodami jest jednorodne.

Graniczna przewodność molowa (równoważnikowa) to przewodność molowa (równoważnikowa) w rozcieńczeniu nieskończenie wielkim (gdy stężenie dąży do zera).

słaby elektrolit

mocny elektrolit

[(mol/dm³)^1/2]

CH₃COONa

CH₃COOH

L_o

 [Sm²mol^-1]

Jony w roztworze w polu elektrycznym wędrują niezależnie od siebie, a przewodnictwo roztworu elektrolitu jest sumą przewodnictw pochodzących od poszczególnych jonów znajdujących się w roztworze.

F_

F_el

Ruchliwość jonu to szybkość poruszania się jonu w polu elektrycznym o natężeniu jednostkowym.

H

H

O

+

H

H

H

O

H

H

H

O

H

H

H

O

+

+

+

+

+

+

_

+

H

H

H

H

O

H

H

O

H

H

O

H

H

O

-

-

H

H

O

+

H

O

H

O

+

H

H

H

O

+

_

+

H

H

O

+

H

O

H

O

+

H

H

H

O

+

Liczba przenoszenia jonu to stosunek ładunku przeniesionego przez jony danego znaku do całkowitego ładunku przeniesionego przez roztwór.

---