Ćwiczenie nr 1

PODSTAWOWE CZŁONY

UKŁADÓW STEROWANIA I

Laboratorium Automatyki i Sterowania

Zakład Energoelektroniki i Sterowania

1. Cel ćwiczenia

Celem ćwiczenia jest doświadczalne poznanie właściwości dynamicznych podstawowych członów układów sterowania oraz właściwości wzmacniacza operacyjnego.

2. Wiadomości ogólne

Analizując układy fizyczne można zauważyć, że istnieją pewne czynniki zewnętrzne, mające wpływ na ich stan, w którym znajduje się ten układ.

Czynniki zewnętrzne, na których wartość można w sposób świadomy wpływać, przyjęto nazywać wielkościami wejściowymi, lub wymuszeniami, te zaś, których nie kontroluje się, nazywa się zazwyczaj zakłóceniami.

Możemy również w każdym układzie wyróżnić pewne wielkości zależne bezpośrednio od stanu układu, a więc pośrednio od wielkości wejściowych i zakłóceń, których wartości są z jakichś względów interesujące. Nazywa się je wielkościami wyjściowymi.

Badanie układu polega zazwyczaj na empirycznym znalezieniu powiązań między wielkościami wyjściowymi i wejściowymi i ewentualnie zakłóceniami. Powiązania te przedstawia się za pomocą odpowiednich równań lub wykresów. Zależności między tymi wielkościami, występujące w stanach ustalonych, noszą nazwę charakterystyk statycznych. Zależności wiążące te wielkości w stanach nieustalonych, określają właściwości dynamiczne układu.

Właściwości dynamiczne układu są określone jakościowo przez strukturę układu. Parametry te mogą być skupione lub rozłożone w przestrzeni (np. linia długa), ponadto mogą być stałe lub zmienne w czasie.

Jeżeli wielkości występujące w układzie są powiązane ze sobą za pomocą równań liniowych, to wtedy układ taki nazywamy liniowym.

Podział układów na liniowe i nieliniowe jest bardzo istotny, gdyż układy liniowe posiadają specjalne właściwości ułatwiające analizę i umożliwiające stosowanie prostych metod badania właściwości dynamicznych. Dla układów liniowych obowiązuje zasada superpozycji. Polega ona na tym, że wypadkowy przebieg wyjściowy można uzyskać sumując przebiegi wyjściowe wywołane składowymi przebiegu wejściowego.

Metody analityczne badania dynamiki układów regulacji automatycznej są skuteczne na ogół jedynie dla układów liniowych niższych rzędów i dla prostych układów nieliniowych. Dla układów liniowych wyższych rzędów oraz bardziej skomplikowanych układów nieliniowych, metody analityczne są uciążliwe i mało przydatne. Dla takich układów najskuteczniejszą metodą badania właściwości dynamicznych jest metoda modelowania.

Istota modelowania polega na odwzorowaniu badanego układu za pomocą modelu opisywanego tymi samymi równaniami matematycznymi, co rozpatrywany układ.

Modelowanie matematyczne realizuje się zwykle na analogowych układach elektronicznych, pneumatycznych lub mechanicznych. Podstawowym elementem układów analogowych są wzmacniacze operacyjne objęte odpowiednimi torami sprzężeń zwrotnych.

Obejmując wzmacniacz operacyjny pewnymi torami liniowymi sprężeń zwrotnych można zamodelować podstawowe człony dynamiczne.

Każdy liniowy układ, który chcemy zamodelować można za pomocą pewnych metod przedstawić w postaci kombinacji podstawowych członów dynamicznych, sprzężeń zwrotnych oraz węzłów sumacyjnych i zaczepowych. Z tego właśnie powodu bardzo ważną rzeczą w technice modelowania jest umiejętność modelowania prostych członków dynamicznych za pomocą wzmacniaczy operacyjnych.

Wzmacniacz operacyjny

Wzmacniacz operacyjny posiada następujące właściwości:

1. bardzo duży współczynnik wzmocnienia napięciowego (rzędu
   ),

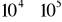
2. dużą rezystancję wejściową, rzędu 1 MΩ

3. małą rezystancję wyjściową, poniżej kilkunastu Ω,

4. dużą stabilność zera,

5. szerokie pasmo przenoszonych częstotliwości, zaczynających się od zera (wzmacniacz musi wzmacniać również prąd stały),

6. dwupolarną charakterystykę statyczną, liniową w dużym zakresie amplitud wejściowych, (dwupolarną charakterystykę statyczną wzmacniacza nazywamy charakterystykę, obejmującą zakres zarówno dodatnich, jak i ujemnych napięć wejściowych),

7. musi odwracać fazę o 180 ^o_.

Wzmacniacz operacyjny musi odwracać fazę o 180 ^o w tym celu, aby można było modelować za pomocą wzmacniaczy operacyjnych układy z ujemnym sprzężeniem zwrotnym. W przypadku, gdy liczba wzmacniaczy operacyjnych, użytych do zamodelowania toru jest nieparzysta uzyskuje się sprzężenie ujemne (inwersja), jeżeli parzysta parzyste sprzężenie dodatnie.

3. Podstawowe człony dynamiczne układów sterowania i ich modele

W tym punkcie zostaną omówione następujące człony dynamiczne:

• proporcjonalny,

• całkujący idealny,

• różniczkujący idealny.

1. Człon proporcjonalny (bezinercyjny)

Wielkość wyjściowa regulatora - sterowanie y(t) jest proporcjonalne do wielkości wejściowej U(t). Człon bezinercyjny proporcjonalny (wzmocnienie) jest opisywany równaniem:

,

transmitancją operatorową

.

transmitancją widmową (amplitudowo-fazową)

.

Parametr k nosi nazwę współczynnika wzmocnienia.

Człon ten ma oznaczenie :

Na rysunku 1 pokazano schemat blokowo-ideowy członu proporcjonalnego a na rysunku 2 odpowiadającą mu charakterystykę skokową
.

Rys.1. Model członu proporcjonalnego

Rys.2. Charakterystyka skokowa członu proporcjonalnego

Uzyskuje się w ten sposób model członu o transmitancji operatorowej,

,

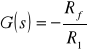
która jest transmitancją członu proporcjonalnego.

2. Człon całkujący idealny

Równanie, transmitancja operatorowa i widmowa członu całkującego mają postać:

,

,

.

parametr k przyjęto nazywać współczynnikiem wzmocnienia prędkościowego.

Człon ten ma następujące oznaczenie

Schemat blokowo-ideowy modelu członu całkującego idealnego przedstawia rysunek 3, a jego charakterystykę skokową pokazano na rysunku 4.

Rys.3. Model członu całkującego idealnego

Rys.4. charakterystyka skokowa członu całkującego idealnego

Transmitancja operatorowa opisująca człon całkujący idealny ma postać:

,

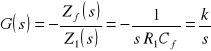
przy czym we wzorze przyjęto, że
.

3. Człon różniczkujący idealny

Człon różniczkujący idealny można opisać za pomocą następującego równania, transmitancji operatorowej i widmowej.

,

,

.

Oznaczenie członu różniczkującego pokazano na schemacie:

Schemat blokowo-ideowy modelu członu różniczkującego przedstawiono na rysunku 5 a jego charakterystykę skokową na rysunku 6.

Rys.5. Model członu różniczkującego idealnego

Rys.6. charakterystyka skokowa członu różniczkującego idealnego

Transmitancja operatorowa członu różniczkującego idealnego ma postać:

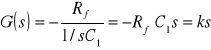
Iloczyn
jest wzmocnieniem modelu członu.

4. Pomiary

1. Zbadać inwersyjne właściwości wzmacniacza operacyjnego dla przebiegu sinusoidalnego, prostokątnego i piłokształtnego.

Układ pomiarowy dla p. 4.1 i p. 4.2

2. Pomiar wzmocnienia napięcia wzmacniacza w funkcji częstotliwości napięcia sinusoidalnego (dla częstotliwości akustycznych).

3. Modelowanie prostych członów dynamicznych. Posługując się odpowiednimi opornikami i kondensatorami zamodelować i zarejestrować przebiegi czasowe w uzyskane w odpowiedzi na wymuszone skokowe dla następujących układów:

• członu proporcjonalnego (idealnego),

• członu całkującego idealnego,

• członu różniczkującego idealnego.

5. Sprawozdanie

Sprawozdanie powinno zawierać:

1. schematy układów pomiarowych,

2. wyniki pomiarów i zarejestrowane przebiegi,

3. wykresy,

4. dyskusja i wnioski.

---