Bartosz Gabruk

termin zajęć: czwartek 7:30-9:00

data oddania sprawozdania: 29.04.2010 (poprawione)

Ćw. 44A Pomiar zależności oporu metali

i półprzewodników od temperatury

1. Wstęp teoretyczny

Przepływ prądu w metalu polega na uporządkowanym ruchu elektronów będących swobodnymi nośnikami ładunku. Zakłócenie przepływu strumienia elektronów powodujące spadek konduktywności metalu (a tym samym wzrost rezystancji) wywoływane jest przez dwie podstawowe przyczyny:

- w zakresie wysokich temperatur wzrasta amplituda drgan sieci krystalicznej, a tym samym przekrój czynny na rozpraszanie co powoduje osłabienie strumienia swobodnych nośników ładunku, czyli wzrost rezystancji. Dla czystych metali jednoskładnikowych zależność oporu elektrycznego od temperatury jest w przybliżeniu liniowa:

Rt=R0(1+0t)

Ro - rezystancja w temperaturze 0C,

Rt - rezystancja w temperaturze t,

o - temperaturowy współczynnik rezystancji w zakresie od 0 do t C:

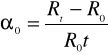
- rozpraszanie swobodnych nośników na wszelkich defektach sieciowych. W czystych jednoskładnikowych metalach ten typ rozpraszania jest dominujący w niskich temperaturach, natomiast w temperaturze pokojowej i wyższych nie ma większego znaczenia.

Dla półprzewodników prawdziwe są powyższe spostrzeżenia o rozpraszaniu swobodnych nośników w metalach, z tym że w niskich temperaturach głównymi defektami strukturalnymi są zjonizowane atomy domieszek. Dlatego w półprzewodnikach można zauważyć silną, wykładniczą zależność konduktancji od temperatury:

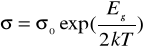
Eg - szerokość pasma wzbronionego,

k= 1,38*10-23 JK - stała Boltzmanna,

T - temperatura w kelvinach,

o -stała niezależna od temperatury.

Z powyższego wzoru można bezpośrednio wyznaczyć zależność oporu od temperatury:

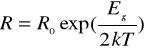
Ro - stała zależna od rodzaju i wymiarów geometrycznych półprzewodnika. Oznacza ona rezystancję jaką miałby w nieskończenie dużej temperaturze.

W celu wyliczenia szerokości pasma zabronionego Eg należy wyznaczyć wykres zależności lnR=f(1000/T), odczytać z niego tg kąta nachylenia odcinka prostoliniowego charakterystyki i ostatnie równanie zlogarytmować stronami:

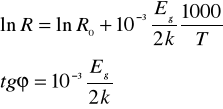
a następnie wyznaczyć Eg:

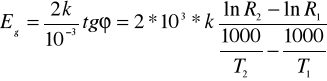
w powyższym wzorze (lnR1,1000/T1) i (lnR2,1000/T2) to współrzędne punktów na początku i końcu prostoliniowego odcinka charakterystyki ln=f(1000/T).

3. Przebieg pomiarów

Próbka	1[opór w kΩ]	2 [opór w MΩ]	3 [opór w Ω]	4 [opór w Ω]
Temperatura ( ̊C)
21,5	1,897	64,7	39,9	108,7
25,1	1,918	62,6	37,5	109,8
30,0	1,958	56,1	33,6	111,6
35,0	1,984	51,5	29,9	113,4
40,0	2,048	36,8	26,5	114,9
45,0	2,038	36,8	21,8	116,9
50,0	2,160	36,2	18,8	118,6
55,0	2,184	35,6	16,7	120,5
60,0	2,236	36,8	15,4	122,2
65,0	2,301	37,7	13,6	123,9
70,0	2,373	36,8	10,5	126,1
75,0	2,424	36,9	9,8	127,7
80,0	2,486	36,8	9,1	129,5
85,0	2,548	36,8	8,0	131,1
90,0	2,583	36,9	7,0	133,0
95,0	2,655	36,8	6,5	134,6
100,0	2,710	35,1	5,7	136,5

Na podstawie wyników pomiarów oraz wiadomości zawartych we wstępie, można stwierdzić, że:
próbka 1 i 4 - zależność rezystancji od temperatury ma charakter liniowy - próbka wykonana z metalu

próbka 2 i 3 - wzrost temperatury powoduje zmniejszanie się rezystancji - próbki są półprzewodnikami4. Opracowanie wyników pomiaru

W celu zamiany temperatury w C na temperaturę wyrażoną w K należy dokonać przekształcenia :

T=t+273,15

Następnie można przystąpić do sporządzenia wykresów:

Rm=f(t)

ln Rt=f(1000/T)

a później wyznaczyć szerokość pasma zabronionego w półprzewodniku:

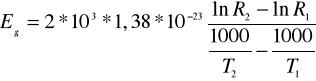
oraz temperaturowy współczynnik rezystancji metalu przyjmując jako rezystancję odniesienia rezystancję w temperaturze 25C:

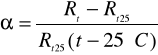
Próbka 1

t	Rm	ΔRm	a	Δa	b	Δb	α	Δα	Δα/α
̊C	kΩ	kΩ	kΩ/ ̊C	kΩ/ ̊C	kΩ	kΩ	̊C^-1	̊C^-1	%
21,5	1,897	0,011	27,5	2,0	1,63	0,02	16,9	1,5	8,88
25,1	1,918	0,011
30,0	1,958	0,011
35,0	1,984	0,011
40,0	2,048	0,012
45,0	2,038	0,012
50,0	2,160	0,012
55,0	2,184	0,012
60,0	2,236	0,013
65,0	2,301	0,013
70,0	2,373	0,013
75,0	2,424	0,014
80,0	2,486	0,014
85,0	2,548	0,014
90,0	2,583	0,014
95,0	2,655	0,015
100,0	2,710	0,015

Wartości a, Δa, b, Δb oraz obliczone za pomocą funkcji REGLINP w programie Excel.

Przykładowe obliczenia:

ΔR_m= (±0,5% rdg + 1dgt) = 1,897*(0,5/100) = 0,009485≈0,010 + 0,001 = 0,011Ω

α = a/b = 27,40373/1,621638 = 16,89880 C^-1

Wyznaczenie niepewności Δα metodą różniczki zupełnej:

*
+
*

=
*
+
*
= 1,434≈1,5

Próbka 2

t	T	1000/T	Rs	ΔRs	LnRs	ΔlnR	A	ΔA	Eg		ΔEg
˚C	K	K^-1	MΩ	MΩ			K	K	J	eV	J	eV
21,5	294,65	3,40	64,7	0,5	4,170	0,008	0,715513	0,07	1,976*10^-20	0,123	0,20*10^-20	0,013
25,1	298,25	3,36	62,6	0,5	4,137	0,008
30,0	303,15	3,30	56,1	0,4	4,027	0,008
35,0	308,15	3,25	51,5	0,4	3,942	0,008
40,0	313,15	3,20	36,8	0,3	3,606	0,009
45,0	318,15	3,15	36,8	0,3	3,606	0,009
50,0	323,15	3,10	36,2	0,3	3,589	0,009
55,0	328,15	3,05	35,6	0,3	3,572	0,009
60,0	333,15	3,01	36,8	0,3	3,606	0,009
65,0	338,15	2,96	37,7	0,3	3,630	0,009
70,0	343,15	2,92	36,8	0,3	3,606	0,009
75,0	348,15	2,88	36,9	0,3	3,608	0,009
80,0	353,15	2,84	36,8	0,3	3,606	0,009
85,0	358,15	2,80	36,8	0,3	3,606	0,009
90,0	363,15	2,76	36,9	0,3	3,608	0,009
95,0	368,15	2,72	36,8	0,3	3,606	0,009
100,0	373,15	2,68	35,1	0,3	3,558	0,009

Przykładowe obliczenia:

T = t + 273,15 = 21,5+273,15 = 294,65K

1000/T = 1000/294,65 ≈ 3,40 K^-1

ΔR_s= 64,7*(0,5/100) = 0,4 + 0,1 = 0,5 MΩ

[dokładność multimetru: (±0,5% rdg + 1 dgt)]

E_g= 2*10³*k*A, gdzie k - stała Bolzmana = 1,3806 10-23 J/K

E_g= 2*10³*k*(0,715513)= 1,976*10^-20J

1 J = 0,62415 · 10¹⁹ eV

1,976*10^-20J = 0,123 eV

y = lnR

*
=

Obliczenie niepewności szerokości przerwy energetycznej metodą różniczki zupełnej:

=
*∆A = 0,20*10^-20

Próbka 3

t	T	1000/T	Rs	ΔRs	LnRs	ΔlnR	A	ΔA	Eg		ΔEg
˚C	K	K^-1	Ω	Ω			K	K	J	eV	J	eV
21,5	294,65	3,40	39,9	0,3	3,686	0,008	2,810299	0,050994	7,76 *10^-20	0,484	1,43*10^-20	0,021
25,1	298,25	3,36	37,5	0,3	3,624	0,008
30,0	303,15	3,30	33,6	0,3	3,514	0,008
35,0	308,15	3,25	29,9	0,3	3,398	0,008
40,0	313,15	3,20	26,5	0,2	3,277	0,008
45,0	318,15	3,15	21,8	0,2	3,082	0,009
50,0	323,15	3,10	18,8	0,2	2,934	0,011
55,0	328,15	3,05	16,7	0,2	2,815	0,012
60,0	333,15	3,01	15,4	0,2	2,734	0,013
65,0	338,15	2,96	13,6	0,2	2,610	0,015
70,0	343,15	2,92	10,5	0,1	2,351	0,010
75,0	348,15	2,88	9,8	0,1	2,282	0,010
80,0	353,15	2,84	9,1	0,1	2,208	0,011
85,0	358,15	2,80	8,0	0,1	2,079	0,012
90,0	363,15	2,76	7,0	0,1	1,946	0,014
95,0	368,15	2,72	6,5	0,1	1,872	0,015
100,0	373,15	2,68	5,7	0,1	1,740	0,018

Próbka 4:

t	Rm	ΔRm	a	Δa	b	Δb	α	Δα	Δα/α
̊C	Ω	Ω	Ω/ ̊C	Ω/ ̊C	Ω	Ω	̊C^-1	̊C^-1	%
21,5	108,7	0,6	0,35621	0,001261	100,88	0,08173	0,00353	1,5*10^-5	0,42
25,1	109,8	0,07
30,0	111,6	0,07
35,0	113,4	0,07
40,0	114,9	0,07
45,0	116,9	0,07
50,0	118,6	0,07
55,0	120,5	0,07
60,0	122,2	0,07
65,0	123,9	0,07
70,0	126,1	0,07
75,0	127,7	0,07
80,0	129,5	0,07
85,0	131,1	0,08
90,0	133,0	0,08
95,0	134,6	0,08
100,0	136,5	0,08

5. Wyniki końcowe

6. Wnioski

Zależność oporu metali od temperatury jest liniowa, co potwierdzają wykonane wykresy.

Zależność oporu półprzewodników od temperatury jest wykładnicza, a liniowa zależność na wykresie widoczna jest dopiero po zlogarytmowaniu równania zależności.

---