Wyznaczanie momentu bezwładności i sprawdzanie twierdzenia Steinera.
TARCZA |
||||||||
|
|
|
masa tarczy: |
0,414 |
kg |
|
|
|
π = |
3,14 |
|
|
∆m= |
0,001 |
kg |
|
|
g= |
9,81 |
m/s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
wymiary [m] |
tolerancja ± [m] |
|
|
|
|
||
|
1 |
2 |
3 |
|
|
|
|
|
2d = |
0,115 |
0,0653 |
0,0154 |
0,0001 |
|
|
|
|
d = |
0,0575 |
0,0327 |
0,0077 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
czasy [s] |
|
|
|
|
|
||
|
63 |
65 |
109 |
tolerancja ± [s] |
|
|
|
|
|
okresy [s] |
|
|
|
|
|
||
|
0,63 |
0,65 |
1,09 |
0,001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
stąd: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
momenty bezwladności [kg*m2] |
|
|
|
|
|
||
|
1 |
2 |
3 |
|
|
|
|
|
I= |
23,48 |
14,19 |
9,38 |
|
|
|
|
|
∆I= |
0,17 |
0,12 |
0,16 |
|
|
|
|
|
|
z twierdzenia Steinera: |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
stąd: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
momenty bezwładności [kg*m2] |
wartość średnia |
|
|
|
|
||
|
1 |
2 |
3 |
|
|
|
|
|
I0= |
9,79 |
9,78 |
9,14 |
9,57 |
|
|
|
|
∆I0= |
0,25 |
0,16 |
0,17 |
0,19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I0=(9,57 ±0,19)*10-5 kg*m2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
MOMENTY BEZWLADNOŚCI PIERŚCIENI |
||||||||
|
|
|
|
|
|
|
|
|
|
|
pierścień pierwszy |
|
|
|
|
|
|
|
|
|
|
masa: |
0,8 |
kg |
|
|
|
|
|
|
∆m= |
0,001 |
kg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Wymiary [m] |
|
|
|
||||
|
D |
0,145 |
R |
0,0725 |
tolerancja ± [m] |
|
|
|
|
d |
0,115 |
r |
0,0575 |
0,0001 |
|
|
|
|
czasy [s] |
|
|
|
|
|
||
|
1 |
2 |
3 |
|
|
|
10-3 |
0,001 |
|
72 |
74 |
71 |
wartość średnia [s] |
tolerancja ± [s] |
103 |
1000 |
|
|
okresy [s] |
|
|
|
|
|||
|
0,72 |
0,74 |
0,71 |
0,723 |
0,001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
stąd: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
I= |
5,93 |
10-3 kg*m2 |
|
|
|
|
|
|
∆I= |
0,00095 |
10-3 kg*m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z twierdzenia Steinera: |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
stąd: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
I0= |
3,28 |
10-3 kg*m2 |
|
|
|
|
|
|
∆I0= |
0,004 |
10-3 kg*m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
I0= |
3,43 |
10-3 kg*m2 |
|
|
|
|
|
|
∆I0= |
0,015 |
10-3 kg*m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Walec |
|
|
|
|
|
|
|
|
|
|
masa: |
1401 |
g |
|
|
|
|
|
|
|
1,401 |
kg |
tolerancja ± [m] |
|
|
|
|
|
∆m= |
0,001 |
kg |
|
|
|
2R= |
135 |
mm |
R= |
67,5 |
m |
0,0001 |
|
|
2r= |
102 |
mm |
r= |
51 |
m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
czasy [s] |
|
|
|
|
|
||
|
1 |
2 |
3 |
|
|
|
|
|
|
69 |
69 |
69 |
wartość średnia [s] |
tolerancja ± [s] |
|
|
|
|
okresy [s] |
|
|
|
|
|||
|
0,69 |
0,69 |
0,69 |
0,69 |
0,001 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10-3 |
0,001 |
|
|
|
|
|
|
|
103 |
1000 |
|
|
|
stąd: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
I= |
1,61 |
10-3 kg*m2 |
|
|
|
|
|
|
∆I= |
0,02 |
10-3 kg*m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z twierdzenia Steinera:
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
stąd: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
I0= |
0,82 |
10-3 kg*m2 |
|
|
|
|
|
|
∆I0= |
0,02 |
10-3 kg*m2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
I0= |
0,84 |
10-3 kg*m2 |
|
|
|
|
|
|
∆I0= |
0,01 |
10-3 kg*m2 |
|
|
|
|
![]()
![]()
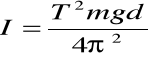
![]()
![]()
![]()
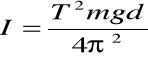
![]()
![]()
![]()
![]()
![]()
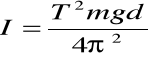
![]()
Wyszukiwarka
Podobne podstrony:
Fifyka komputerowa, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Elektronika 03, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Zadania z Fizyki
fiele25, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
Pomia napięcia powierzchniowego, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, spr
fiele15, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Lab
lista4elektronika(1), Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka
Sprawozdanie 81, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
Sprawozdanie nr12, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fi
Sprawozdanie nr43 fizyka, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdan
Sprawozdanie 12, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizy
LABORATORIUM, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
Sprawozdanie 57c, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fiz
pp25, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, Labora
zas nieoznaczonosci, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, Fizyka II - Popko, fiz
POCHODNA FUNKCJI, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, fiza
76, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, fiza lab
LAB51~1, Mechanika i Budowa Maszyn PWR MiBM, Semestr I, Fizyka, laborki, sprawozdania z fizykii, fiz
więcej podobnych podstron