1.Iloczyn wektorowy

Iloczynem wektorowym wektorów niezerowych u i w, nazywamy wektor v taki,że

1. v = |u| |w| sin < (u,w)

2. v jest wektorem prostopadłym do płaszczyzny, w której leżą wektory u i w

3. Jego zwrot jest taki, że układ wektorów v,u,w ma orientację zgodną z przyjętą orientacją w przestrzeni

Zwrot wektora v wyznacza reguła śruby prawoskrętnej

Iloczyn wektorowy możemy obliczyć jako wyznacznik macierzy zbudowanej z macierzy wektorów składowych. V[vx,vy,vz] w[wx,wy,wz] to wtedy u x w = v

Moment siły to iloczyn wektorowy siły i ramienia.

Iloczyn wektorowy dwóch wektorów równoległych jest równy 0.

2. Dywergencja

Operator różniczkowy, który z wektora tworzy skalar:

Przykład: (jedno z praw Maxwella: dywergencja pola elektrycznego równa się gęstości przestrzennej ładunku);

W przypadku pola elektrycznego takimi "źródłami" pola są ładunki, dlatego dywergencja pola elektrycznego jest proporcjonalna do gęstości ładunku w danym punkcie przestrzeni (różniczkowe prawo Gaussa).

Pole wektorowe o zerowej dywergencji nazywamy bezźródłowym. Przykładem takiego pola jest pole magnetyczne

3.Gradient

Operator różniczkowy, który z wielkości skalarnej tworzy wektor:

W fizyce gradientem energii potencjalnej jest siła, a potencjału (np elektrycznego, grawitacyjnego) jest natężenie tego pola.

4. Rotacja

Operator różniczkowy, który z wektora tworzy wektor:

Przykład- rotacja momentu magnetycznego

5. Tensor

Tensor - uogólnienie pojęcia wektora; wielkość, której własności pozostają identyczne niezależnie od wybranego układu współrzędnych.

Wektor = tensor pierwszego rzędu;

Tensor drugiego rzędu ustala zależność między wektorami.

Przykłady tensorów w fizyce:

• skalary: temperatura, masa, energia, gęstość, liczba cząstek i wiele innych,

• wektory: prędkość, siła, wektor położenia, przyspieszenie i wiele innych,

• pseudowektory: moment pędu, prędkość kątowa, przyspieszenie kątowe

• tensory drugiego rzędu: tensor pola elektromagnetycznego, tensor odkształcenia, tensor naprężenia w ciele stałym itp.,

• spinory: spin elektronu, spiny fermionów.

6. Klasyfikacja ruchów:

Ruch - zmiana położenia ciała odbywająca się w czasie, względem jakiegoś układu odniesienia

Ruchy klasyfikuje się określając tor ruchu oraz zmiany wartości prędkości.

Podział ze względu na toru ruchu:

• prostoliniowy (poruszanie się po linii prostej),

• krzywoliniowy (poruszanie się po linii krzywej),

• po okręgu - rozpatrywany jako najprostszy przypadek ruchu krzywoliniowego,

• po elipsie - ruch w polu sił centralnych,

• po paraboli - ruch w polu jednorodnym,

• inne (powyższe są najpopularniejsze).

Podział ze względu na wartości prędkości:

• jednostajny - prędkość nie zmienia się, r(t)=ro+vot

• zmienny - prędkość zmienia się,

• jednostajnie zmienny - zmiany prędkości są jednakowe w jednakowych przedziałach czasu,

• przyspieszony - prędkość zwiększa się, r(t)=ro+vot+At^2/2, v(t)=vo+at

• opóźniony - prędkość maleje,

• niejednostajnie zmienny.

7. Rzut ukośny (przykład ruchu płaskiego, ruch w polu jednorodnym, możemy go traktować jako złożenie dwóch ruchów prostoliniowych, ma stałe przyspieszenie g i dowolnie skierowaną prędkość vo)

x

y

L

H



v₀

v_0y

g

v_0x

Korzystając z zasady superpozycji (nakładanie się sił):

Ruch w kierunku „x”: jednostajny z prędkością

Ruch w kierunku „y”: jednostajnie opóźniony z prędkością początkową i przyspieszeniem

Trajektoria ruchu:

Parametry toru:

- zasięg L:

(z warunku: y=0)

- maksymalna wysokość wzniesienia H:

(z warunku: v_y=0)

8.Wielkości kinematyczne w ruchu po okręgu (najprostszy przykład ruchu krzywoliniowego)

- prędkość kątowa (pseudowektor, wielkość opisująca ruch po okręgu, W=d fi / dt rad/s

- przyspieszenie kątowe e=dw(omega)/dt pseudowektor rad/s^2

- okres (czas potrzebny na przebycie długości obwodu okręgu) T=2II/W(omega)

- częstotliwość (liczba cykli w jednostce czasu) f=1/T

- siła dośrodkowa, przyspieszenie dośrodkowe

Ruch jednostajny po okręgu

Ruch po torze o kształcie okręgu z prędkością o stałej wartości, tzn.
. Ruch jednostajny po okręgu jest ruchem niejednostajnie przyspieszonym, tzn. kierunek i zwrot wektorów przyspieszenia
i prędkości
zmieniają się cały czas w trakcie ruchu, nie zmieniają się natomiast ich wartości.

Ruch jednostajny po okręgu może być także definiowany jako ruch po okręgu ze stałą prędkością kątową  

Ruch zmienny po okręgu - ruch po torze o kształcie okręgu ze zmienną wartością prędkości. W zależności od charakteru tej zmiany, można wyróżnić:

• ruch jednostajnie zmienny po okręgu (wartość przyspieszenia kątowego jest stała)

• ruch niejednostajnie zmienny po okręgu - wartość przyspieszenia kątowego opisana jest funkcją w czasie.

Zależność prędkości od czasu w ruchu jednostajnie zmiennym po okręgu wyrażają wzory:

• w przypadku znajomości początkowej i końcowej prędkości kątowej:

• w przypadku znajomości początkowej prędkości kątowej i przyspieszenia kątowego:

gdzie:

α - kąt zakreślony w czasie t,

ω₀ - początkowa prędkość kątowa,

ω - prędkość kątowa po upływie czasu t,

ε - przyspieszenie kątowe,

t - czas trwania ruchu.

9. I. Zasada:

• Każde ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym, dopóki działanie innych ciał nie zmusi go do zmiany tego stanu;

• Ciało pozostaje w stanie spoczynku lub stałej prędkości, gdy jest pozostawione samo sobie (działająca na nie siła wypadkowa jest równa zeru);

Inaczej nazywana zasadą bezwładności.

 obalenie nauki Arystotelesa: gdy nie ma sił zewnętrznych, ciała muszą się zatrzymać!

 istnienie inercjalnego układu odniesienia - czyli właśnie takiego, w którym ciało spoczywa lub porusza się ruchem jednostajnym prostoliniowym jeśli nie działają na niego siły.

II. Zasada:

• Zmiana ruchu jest proporcjonalna do przyłożonej siły i zachodzi w kierunku działającej siły;

• Tempo zmiany pędu ciała jest równe sile wypadkowej działającej na to ciało;

Dla ciał o stałej masie:

a stąd:

Jeżeli na ciało działa stała, niezrównoważona siłą wypadkowa , to ciało to porusza się ruchem jednostajnie przyspieszonym z przyspieszeniem proporcjonalnym do tej siły a odwrotnie proporcjonalnym do masy - miary bezwładności tego ciała.

III. Zasada:

• Działania na siebie dwóch ciał są zawsze równe, lecz przeciwnie skierowane;

• Gdy dwa ciała oddziałują wzajemnie, to siła wywierana przez ciało drugie na pierwsze jest równa i przeciwnie skierowana do siły, jaką ciało pierwsze działa na drugie ciało;

Te siły oddziaływania między ciałami nazywane są siłami reakcji (albo: siłami oddziaływania).

Uwaga: siły reakcji działają na INNE ciała, więc nie można powiedzieć, że one się równoważą!

10. Środek masy (punkt, w którym skupiona jest cała masa w opisie układu, pozwala na opis ruchu skomplikowanej bryły, bardzo często mylony ze środkiem ciężkości)

 Każde ciało można traktować jako układ punktów materialnych. Dlatego pęd ciała możemy obliczyć jako sumę pędów wszystkich punktów materialnych ciała:

 Podstawiając wyrażenie na prędkość każdego punktu materialnego:

 Środkiem masy albo środkiem bezwładności układu punktów materialnych nazywamy punkt, którego położenie dane jest wzorem:

gdzie:

Środek masy układu porusza się jak punkt materialny, w którym skupiona jest cała masa układu, i na który działa siła, równa wypadkowej sił zewnętrznych przyłożonych do układu.

 Środek ciężkości ciała to punkt przyłożenia wypadkowej sił ciężkości („ciężarów”) wszystkich punktów materialnych ciała. Gdy wielkość (przyspieszenie grawitacyjne) jest jednakowa dla wszystkich punktów układu, mamy: .

11. Moment bezwładności

Moment bezwładności to miara bezwładności ciała w ruchu obrotowym względem określonej, ustalonej osi obrotu. Im większy moment, tym trudniej zmienić ruch obrotowy ciała, np. rozkręcić dane ciało lub zmniejszyć jego prędkość kątową.

Definicja

Moment bezwładności ciała zależy od wyboru osi obrotu, od kształtu ciała i od rozmieszczenia masy w ciele. Moment bezwładności ma wymiar
. Zwykle mierzy się go w kg·m².

Moment bezwładności punktu materialnego jest iloczynem jego masy i kwadratu odległości od osi obrotu:

gdzie:

- masa punktu;

- odległość punktu od osi obrotu.

Moment bezwładności ciała składającego się z
punktów materialnych jest sumą momentów bezwładności wszystkich tych punktów względem obranej osi obrotu:

Moment bezwładności jest więc miarą bezwładności ciała w ruchu obrotowym (analog masy jako miary bezwładności w ruchu postępowym).

Załóżmy, że znamy moment bezwładności ciała względem pewnej osi obrotu, ale ciało obraca się względem innej osi, równoległej do niej:

d

O

O'

m

Moment bezwładności ciała I względem dowolnej osi O równa się momentowi bezwładności I' tego ciała względem innej, równoległej do niej osi O', powiększonemu o iloczyn masy tego ciała przez kwadrat odległości między tymi osiami:

twierdzenie Steinera

Wniosek: Gdy środek masy ciała oddala się od osi obrotu, to moment bezwładności ciała względem tej osi wzrasta.

12. Zasada zachowania pędu:

W odosobnionym układzie ciał całkowity pęd układu pozostaje stały.

Przez układ odosobniony, zwany też układem zamkniętym, rozumiemy zespół ciał, pomiędzy którymi działają tylko siły wewnętrzne, czyli siły akcji i reakcji, o których mówi III zasada dynamiki.

Zasada zachowania pędu obowiązuje na przykład przy zderzeniach sprężystych i niesprężystych.

• Zderzenia doskonale sprężyste - w ich wyniku ciała nie odkształcają się wzajemnie, a ich energia mechaniczna przed zderzeniem i po zderzeniu pozostaje stała.

• Zderzenia doskonale niesprężyste - w ich wyniku ciała odkształcają się, a część energii mechanicznej zmienia się w chwili zderzenia w energię wewnętrzną. W tym rodzaju zdarzeń nie jest spełniona zasada zachowania energii mechanicznej.

Zasada zachowania pędu:

Pęd zamkniętego układu ciał nie zmienia się z upływem czasu.

 Podobny rezultat osiągniemy, gdy rozważymy działanie siły zewnętrznej a dokładniej: układ sił zewnętrznych, których wypadkową jest . Wtedy:

Zmiana pędu układu jest równa wypadkowej sił zewnętrznych, działających na układ.

 Inna postać sformułowania zasady zachowania pędu:

Suma pędów wszystkich ciał układu w momencie początkowym równa się sumie pędów tych ciał w dowolnym momencie późniejszym.

(Najczęściej stosowana do zagadnienia zderzeń).

13.Zasada zachowania momentu pedu:

Z zasady dynamiki ruchu obrotowego:wynika wprost:

L=r x p wektor położenia i wektor pędu

Jeżeli wypadkowy moment sił zewnętrznych względem nieruchomego punktu ciała równa się zeru, to moment pędu ciała względem tego punktu nie zmienia się w czasie.

 Można pokazać, że również: moment pędu zamkniętego układu ciał względem dowolnego punktu nieruchomego jest stały.

 Podobnie: jeśli siły zewnętrzne dają moment względem nieruchomej osi równy zeru, to moment pędu ciała względem tej osi nie zmienia się podczas ruchu

14. Zasada zachowania energii:

Zasada zachowania energii zwana prawem zachowania energii - empiryczne prawo fizyki. Stwierdza, że całkowita ilość energii w systemie pozostaje stała w czasie. Konsekwencją tego prawa jest, że energia w systemie zamkniętym nie może być utworzona, ani zniszczona. Jedyne może zmienić się forma energii np. podczas spalania wodoru w tlenie energia chemiczna zmienia się w energię cieplną.

Treść zasady

W układzie izolowanym suma wszystkich rodzajów energii układu jest stała (nie zmienia się w czasie).

15. Praca, moc energia:

Energia, praca, moc

 Pęd charakteryzował ruch postępowy ciała, ale nie może być wielkością „miarą” ruchu ciała podczas obrotu wokół osi. Szukamy więc wielkości ogólnej, która mogłaby charakteryzować zdolność ciał do ruchu.

 Energia jest miarą różnych rodzajów ruchu i miarą zdolności ciał do ruchu (nieodłączna cecha materii, zarówno na poziomie molekularnym jak i makroskopowym).

 Każde ciało jest obdarzone energią (ma zapas energii), będącej miarą jego ruchu. Dla scharakteryzowania różnych rodzajów ruchu i różnych rodzajów oddziaływań między ciałami, wprowadzamy różne rodzaje energii: mechaniczną, wewnętrzną, elektromagnetyczną.

 Wzajemne oddziaływanie między ciałami (i elementami jednego ciała) powoduje zmianę energii ciała, możemy więc opisywać to oddziaływanie jako przekazywanie energii.

 W przypadku energii mechanicznej, jej zmianę powoduje wzajemne oddziaływanie między ciałami poprzez siły. Proces zmiany energii ciała pod wpływem działającej na nie siły nazywamy procesem wykonania pracy a przyrost energii ciała w tym procesie to po prostu praca.

 Praca wykonana przez siłę jest wielkością skalarną, liczbowo równą iloczynowi składowej siły w kierunku wykonywanego ruchu przez drogę, przebytą w tym ruchu:

 W przypadku zmiennej siły o dowolnym kierunku względem przesunięcia i dowolnej trajektorii ruchu między punktami A i B, możemy uogólnić powyższy wzór:

 Jeżeli energia E jest przekazywana z jednego ciała do drugiego, to możemy zdefiniować również tempo przekazywania tej energii. Wielkość tę nazywamy mocą:

(dokładniej: jest to moc chwilowa).

 Jeśli ciało porusza się z prędkością v pod działaniem siły F, to możemy obliczyć moc jako:

 Jednostki:

- Siła: niuton

- Energia, praca: dżul

elektronowolt

- Moc: wat

koń mechaniczny

 W mechanice rozróżniamy dwa rodzaje energii: kinetyczną i potencjalną.

 Energia kinetyczna to energia każdego poruszającego się ciała mierzona pracą, jaką trzeba wykonać przy jego hamowaniu do całkowitego zatrzymania.

Jest to twierdzenie o pracy i energii:

Praca wykonana przez zewnętrzną siłę (wypadkową) na drodze od punktu A do punktu B równa się przyrostowi energii kinetycznej ciała.

 Energia kinetyczna jest więc tzw. funkcją stanu jego ruchu (zależy tylko od wartości początkowych i końcowych).

 Energia potencjalna to energia zmagazynowana przez ciało do użycia w przyszłości. Podaje się ją raczej w postaci względnej zmiany (poziom „zera” wyznaczamy arbitralnie) a konkretna jej postać zależy od typu siły, z którą jest związana.

 Jeżeli ciało znajduje się pod działaniem pewnej siły F, to zmianę jego energii potencjalnej U obliczamy jako pracę, którą trzeba wykonać, aby przesunąć to ciało w obecności tej siły

 Siły zachowawcze to takie siły, dla których praca nie zależy od drogi, po której jest wykonywana.

czyli: praca po drodze zamkniętej równa się zeru.

 Przykładem siły niezachowawczej jest np. tarcie.

 Grawitacyjną energię potencjalną (czyli energię potencjalną w polu sił grawitacji) można obliczyć ze wzoru:

gdzie U_Z oznacza energią potencjalną na powierzchni Ziemi (poziom odniesienia), R_Z jest zaś promieniem Ziemi.

 W przypadku, gdy (blisko powierzchni Ziemi) możemy skorzystać z wzoru przybliżonego:

gdzie: - wysokość nad powierzchnią Ziemi.

 Energię potencjalną sprężystą, czyli np. energię rozciągniętej sprężyny, możemy obliczyć wykorzystując wzór na siłę sprężystą (zgodnie z prawem Hooke`a):

gdzie x oznacza wychylenie z położenia równowagi a k jest współczynnikiem proporcjonalności, zależnym od materiału sprężyny.

 Ustalając „zerowy” poziom energii potencjalnej dla x=0 (sprężyna w położeniu równowagi, nierozciągnięta), możemy otrzymać wyrażenie na energię potencjalną sprężyny:

Zauważmy, że wartość energii potencjalnej nie zależy do tego, czy sprężyna jest ściśnięta, czy rozciągnięta.

 Zderzeniem doskonale sprężystym nazywamy takie zderzenie, w wyniku którego energia mechaniczna układu zderzających się ciał nie zamienia się w inne rodzaje energii (np. cieplnej).

Podczas rozwiązywania zagadnień zderzeń sprężystych stosujemy zasadę zachowania energii i zasadę zachowania pędu.

Zasada zachowania energii (kinetyczne tylko, bo potencjalne takie same):

Zasad zachowania pędu:

Zderzenie centralne: wektory prędkości skierowane są wzdłuż jednej prostej.

 Przykładem jest układ ciał podlegający zderzeniu doskonale niesprężystemu - występuje w nim odkształcenie zderzających się ciał powodujące, że po zderzeniu poruszają się one razem z tą sama prędkością.

Podczas rozwiązywania zagadnień zderzeń niesprężystych stosujemy tylko zasadę zachowania pędu.

Energia została rozproszona - wykonana została jej kosztem praca L, potrzebna na:

• „złączenie się” ciał;

• zmianę ich kształtu (kucie metali!);

• przezwyciężanie oporów (np. wbijanie gwoździ młotkiem, pali kafarem);

W przypadku, gdy drugie ciało przed zderzeniem było w spoczynku (v₂=0):

Stąd:

• zmiana kształtu -> m₂ jak największe (duża część energii kinetycznej pierwszego ciała „zużyta” na pracę);

• „wbijanie” -> m₁ jak największe (duża energia kinetyczna układu po zderzeniu).

16. Prawo powszechnego ciażenia:

Prawo powszechnego ciążenia, zwane także prawem powszechnego ciążenia Newtona, głosi, że każdy obiekt we wszechświecie przyciąga każdy inny obiekt z siłą, która jest wprost proporcjonalna do iloczynu ich mas i odwrotnie proporcjonalna do kwadratu odległości między ich środkami.

Wzajemne przyciąganie się ciał jest źródłem jednej z podstawowych sił w fizyce - sił przyciągania, które podlegają prawu powszechnego ciążenia (grawitacji). Prawo to podał Isaac Newton (1687; pierwsze obserwacje już od 1655)

Między każdymi dwoma punktami materialnymi działa siła wzajemnego przyciągania, wprost proporcjonalna do iloczynu mas tych punktów (m₁ i m₂) a odwrotnie proporcjonalna do kwadratu odległości r między nimi.

 W postaci wektorowej prawo to można zapisać jako:

to siła, z jaką punkt „2” działa na punkt „1”, to promień wodzący, łączący punkt drugi z pierwszym.

m₁

m₂

r₁₂

F₁₂

 Współczynnik to stała grawitacji, wyznaczona po raz pierwszy doświadczalnie w 1797 r. przez Henry`ego Cavendisha

17. Prawa Keplera:

Pierwsze prawo

Każda planeta Układu Słonecznego porusza się wokół Słońca po elipsie, w której w jednym z ognisk jest Słońce

Elipsę można opisać na kilka sposobów, w astronomii najczęściej opisuje się elipsy podając ich wielką półoś (a) oraz mimośród (e), który określa stopień spłaszczenia elipsy (im e bliższe zeru, tym elipsa bliższa jest okręgowi). Mimośród elipsy e jest równy stosunkowi długość odcinka c między środkiem, a jednym z ognisk do długości wielkiej półosi:

Mimośrody orbit planet w naszym układzie są w większości niewielkie. Poza Merkurym dla którego mimośród przekracza nieco wartość 0,2, eliptyczności orbit pozostałych planet są poniżej 0,1. Na przykład mimośród elipsy orbity Ziemi wynosi 0,0167 co oznacza, że wielka oś elipsy orbity Ziemi jest dłuższa od krótkiej osi niewiele więcej niż 0,01% jej długości.

Drugie prawo

W równych odstępach czasu, promień wodzący planety poprowadzony od Słońca zakreśla równe pola.

Wynika stąd, że w peryhelium (w pobliżu Słońca), planeta porusza się szybciej niż w aphelium (daleko od Słońca), czyli planeta w ciągu takiego samego czasu przebywa dłuższą drogę (ΔS) w pobliżu peryhelium, niż w pobliżu aphelium.

Na przykład dla orbity Ziemi (mimośród e = 0,01672) prędkość liniowa Ziemi w peryhelium wynosi 30,3 km/s, zaś w aphelium 29,3 km/s.

Trzecie prawo

Stosunek kwadratu okresu obiegu planety wokół Słońca do sześcianu wielkiej półosi jej orbity (czyli średniej odległości od Słońca) jest stały dla wszystkich planet w Układzie Słonecznym

Można to zapisać wzorem:

gdzie:

T₁, T₂ - okresy obiegu dwóch planet,

a₁, a₂ - wielkie półosie orbit tych planet.

Z prawa tego wynika, że im większa orbita, tym dłuższy okres obiegu, oraz że prędkość liniowa na orbicie jest odwrotnie proporcjonalna do pierwiastka promienia orbity (dla orbity kołowej).

18. Siła Coriolisa (definicja, przykłady).

Coriolisa siła, jedna z sił bezwładności działająca na ciało znajdujące się w nieinercjalnym (tu: obracającym się) układzie odniesienia,

F_cor = -2m ω×v,

gdzie m - masa ciała, ω - wektor prędkości kątowej obracającego się układu, v - wektor prędkości liniowej ciała mierzony w obracającym się układzie odniesienia.

Siła Coriolisa spowodowana dziennym ruchem obrotowym działa na poruszające się poziomo na Ziemi ciała, osiągając największe wartości na biegunach (przy ruchu poziomym wektory ω i v są prostopadłe, niezależnie od kierunku v), a jej składowa pozioma zanika na równiku.

Na półkuli północnej powoduje odchylanie się poruszających się poziomo ciał na prawo (odpowiedzialne np. za intensywniejsze podmywanie prawych brzegów rzek), a na półkuli południowej - w lewo.

Siła Coriolisa działa na spadające swobodnie ciała, odchylając je od pionu w kierunku wschodnim. Siła działająca na jednostkową masę nazywa się przyspieszeniem Coriolisa. Jej istnienie zauważył Gaspard Gustave de Coriolis (1792-1843), francuski matematyk.

19. Transformacje Lorentza : (stosujemy do prędkości zbliżonych do prędkości światła, wynikają z niej wszystkie efekty kinematyczne szczególnej teorii względności, jeśli wzajemna prędkość poruszających się układów jest duża mniejsza od prędkości światła pomijamy człon i otrzymujemy transformacje Galileusza)

Lorentza transformacja, Lorentza przekształcenie, przekształcenie matematyczne opisujące transformacje wielkości fizycznych w czasoprzestrzeni czterowymiarowej przy przechodzeniu od jednego inercjalnego układu odniesienia, określonego przez współrzędne przestrzenne x, y, z i współrzędną czasową t, do drugiego, określonego przez współrzędne x', y', z' oraz t'.

W najprostszym przypadku, jeśli układ (x', y', z', t') porusza się jednostajnie w kierunku osi x z prędkością v, to transformacja Lorentza ma postać:

gdzie c - prędkość światła w próżni.

20. Dylatacja czasu:

Dylatacja czasu, jest to zjawisko różnic w pomiarze czasu dokonywanym równolegle w dwóch różnych układach odniesienia, z których jeden przemieszcza się względem drugiego. W praktyce oznacza to, że jeżeli w układzie K' zachodzą dwa równoczesne zdarzenia, to dla obserwatora w K zdarzenia te nie są jednoczesne tylko następują po sobie. W szczególnej teorii względności czasy przebiegu tego samego zjawiska dla różnych obserwatorów są powiązane zależnością:

gdzie:

Δt₀ - czas trwania zjawiska zarejestrowany przez obserwatora spoczywającego względem zjawiska,

Δt - czas trwania tego samego zjawiska zachodzącego w układzie odniesienia pierwszego obserwatora rejestrowany przez obserwatora poruszającego się względem pierwszego z prędkością v,

czynnik Lorentza,

v - względna prędkość obserwatorów,

c - prędkość światła w próżni.

21. Pęd relatywistyczny a pęd klasyczny:

 Klasyczna definicja pędu:

Taka definicja pędu, w połączeniu z transformacją Einsteina dla prędkości nie zapewni nam jednak spełnienia zasady zachowania pędu! ( jest prędkością cząstki).

 Nowa definicja pędu (która zapewni prawdziwość zasady zachowania pędu przy transformacji do dowolnego układu współrzędnych) podana przez Einsteina:

gdzie:

(uwaga! Podobieństwo oznaczeń, ale TO zależy od prędkości cząstki , a nie od prędkości poruszania się układu współrzędnych!).

23. Drgania harmoniczne: opisane funkcją sinusoidalną, najprostszy rodzaj drgań

 Drganie okresowe harmoniczne - położenie ciała opisuje funkcja sinus (bądź kosinus):

 W ruchu harmonicznym:

Prędkość

Przyspieszenie

 Przypomnienie:

Druga zasada dynamiki Newtona:

 Ruch harmoniczny to taki, dla którego:

Siła jest proporcjonalna do wychylenia i przeciwnie do niego skierowana (prawo Hooke'a). (F - siła harmoniczna)

 Ogólne równanie różniczkowe drgań harmonicznych:

 Wielkości opisujące ruch harmoniczny prosty (drgania harmoniczne):

- jest amplitudą drgań (maksymalną zmianą względem położenia równowagi);

- to faza drgań (mierzona w radianach bądź stopniach);

- to częstość kołowa (pulsacja) (w radianach na sekundę);

- to faza początkowa.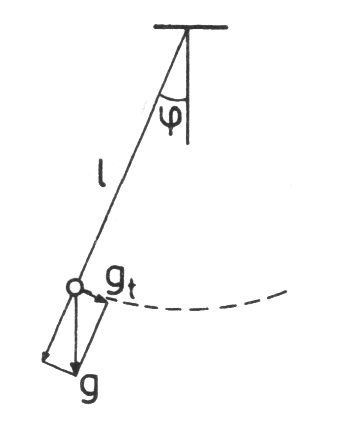

- Częstotliwość drgań: (Hz - herc);

 Wahadło matematyczne:

Punkt materialny, zawieszony na nieważkiej i nierozciągliwej nici;

; ;

 Wahadło fizyczne:

Ciało doskonale sztywne, które pod działaniem własnego ciężaru waha się dookoła osi poziomej, nie przechodzącej przez środek ciężkości ciała;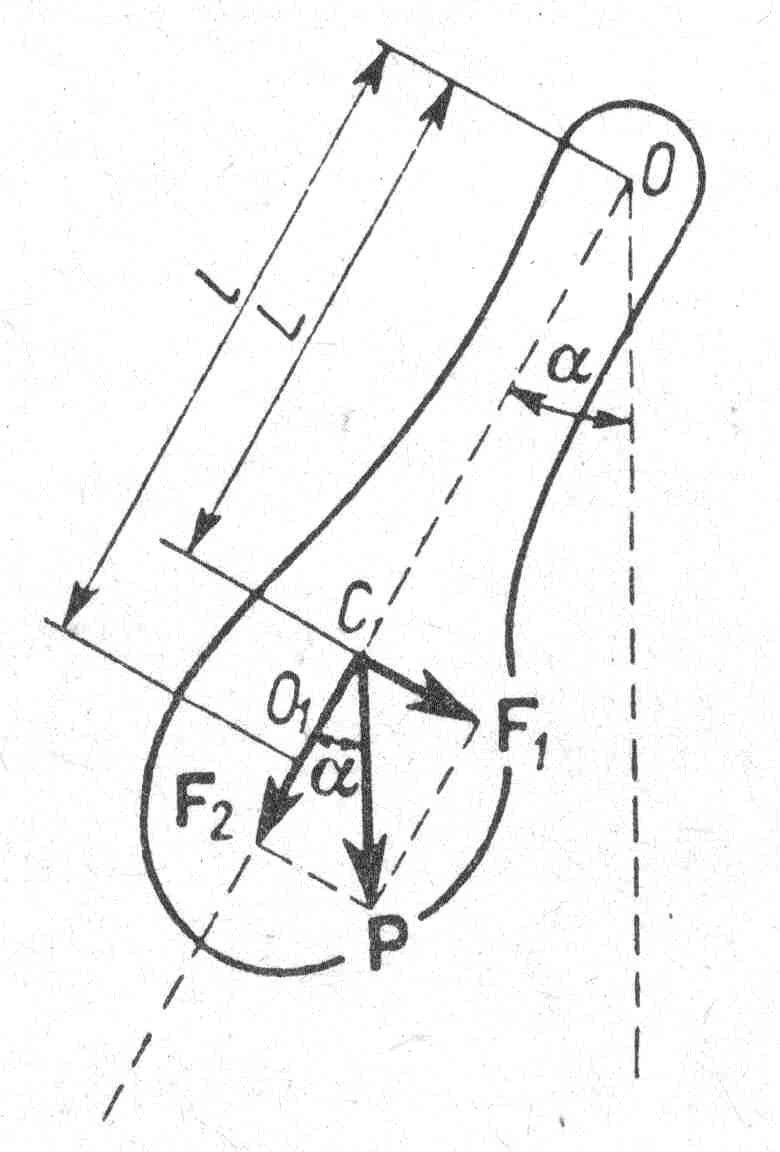

 Sprężyna:

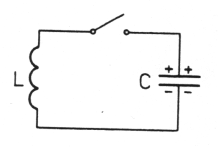
 Obwód LC:

; ;

24. Drgania tłumione i wymuszone:

Drgania wymuszone zachodzą pod wpływem zewnętrznej siły, będącej źródłem energii podtrzymującej drgania.
Siła wymuszająca F_W ma zwykle charakter siły o wartości okresowo zmiennej:
F_W = F_W0sinωt
gdzie: F_W0 - amplituda siły wymuszającej.
Amplituda drgań wymuszonych nie jest stała i zależy od częstości siły wymuszającej ω.
Amplituda drgań wymuszonych wyraża się wzorem:

Drgania tłumione

Amplituda drgań tłumionych maleje na skutek oporów ośrodka, w którym zachodzą drgania.
Drgania tłumione opisuje równanie:

,
gdzie: δ - współczynnik tłumienia. Zależność wychylenia x od czasu dla drgań tłumionych przedstawiona została na rysunku:

25. Rezonans:

Rezonans, zjawisko gwałtownego wzrostu amplitudy drgań układu mechanicznego lub elektrycznego zachodzące, gdy częstość drgań wymuszających zbliża się do częstości drgań własnych.

Zjawisko rezonansu przebiega tym gwałtowniej, im mniejsze jest tłumienie w układzie. Ma decydujące znaczenie dla procesu wydobywania dźwięku w instrumentach muzycznych. Oddziałuje niekorzystnie na wiele typów konstrukcji.

Rezonans mechaniczny to zjawisko polegające na przepływie energii pomiędzy kilkoma (najczęściej dwoma) układami drgającymi. Warunkami koniecznymi do zajścia rezonansu mechanicznego są:

• jednakowa lub zbliżona częstotliwość drgań własnych (lub swobodnych) układów,

• istnienie mechanicznego połączenia między układami.

• Ze zjawiskiem rezonansu spotykamy się jadąc np. autobusem. Przy pewnej prędkości kątowej obrotów silnika, szyby lub niektóre części karoserii zaczynają silnie drgać.

• Rezonans ma decydujące znaczenie dla procesu powstawania i wzmacniania dźwięku w instrumentach muzycznych np.: Wykorzystany jest w akustyce poprzez stosowanie pudeł rezonansowych w instrumentach muzycznych, np. w gitarze. Gdy uderzymy strunę gitary do pudła rezonansowego dochodzą drgania wytwarzane przez uderzoną strunę. W pudle rezonansowym powstają fale stojące o częstotliwościach drgań struny będące składowym harmonicznym częstotliwości podstawowej wytworzonej przez strunę. Składowe o różnych częstotliwościach zostają wzmocnione w różnym stopniu nadając ostatecznie charakterystyczną barwę dźwiękowi danego instrumentu.

• Śpiewak wydając ton o określonej częstotliwości może wywołać drgania szklanego naczynia. Jeśli trwa to dostatecznie długo, energia zaabsorbowana (czyli pochłonięta) przez szkło może wywołać drgania dostatecznie silne do tego, aby szkło pękło.

26. Fala (definicja, równanie falowe, wielkości).

 Falą nazywamy każde rozprzestrzeniające się zaburzenie (odkształcenie, drgania).

 Fala poprzeczna - gdy drgania zachodzą w kierunku prostopadłym do kierunku rozchodzenia się fali.

 Fala podłużna - gdy drgania zachodzą w kierunku równoległym do kierunku rozchodzenia się fali.

Równanie falowe:

Rozwiązanie ogólne: dowolna funkcja argumentu

 Przykład fali biegnącej po strunie:

dla dowolnej, ustalonej wartości t:

- to długość fali (odległość między powtarzającymi się fragmentami fali, np. „grzbietami”);

- prędkość przesuwania się „grzbietu” fali, czyli prędkość fazowa fali;

 Związki między prędkością, okresem i długością fali:

- okres fali; - częstość kołowa; - częstotliwość;

 Liczba falowa (wektor falowy):

 Prędkość fazowa:

Przykład: równanie falowe dla metalowej struny o liniowej gęstości masy  i naprężeniu działającym na strunę T:

czyli:

27. Temperatura

TEMPERATURA

 Bezwzględna skala temperatur - skala Kelvina - oparta jest na definicji punktu „0” jako „zera” energii kinetycznej, kiedy ustaje wszelki ruch cząsteczek, i jednostce temperatury - kelwinie (K) - równym stopniowi Celsjusza. „Zero bezwzględne” to ok. -273 stopnie w bardziej znanej na co dzień skali Celsjusza.

 Skala Celsjusza została stworzona na bazie dwóch punktów, charakterystycznych dla wody: temperaturze zamarzania (przyjętej za „0”) i temperaturze wrzenia (jako „100”). Jednostką jest więc 1/100 tego przedziału, zwana stopniem Celsjusza (C).

 W krajach anglosaskich powszechnie używana jest skala Fahrenheita - jeden stopień tej skali równa się 5/9 stopnia Celsjusza.

 Inne spotykane skale temperatur - Reaumura, Rankine'a - mają już dziś tylko znaczenie historyczne.

TERMOMETRY

 Mikroskopowa definicja temperatury (miara średniej energii kinetycznej cząsteczek) nie nadaje się do pomiarów. Pod tym względem lepsza jest definicja makroskopowa, wiążąca inne, mierzalne parametry gazu doskonałego - ciśnienie i objętość - z szukaną temperaturą.

 Termometry „objętościowe” związane są ze zmianą wymiarów ciała ze zmianą temperatury (rozszerzalność liniowa).

Najprostszym przykładem jest termometr rtęciowy. Dokładniejszym przyrządem tego typu jest termometry gazowy stałego ciśnienia. Pomiar temperatury polega na pomiarze objętości (wymiaru liniowego) rozszerzającego się ośrodka.

 Termometry gazowe stałej objętości bazują na pomiarze zmian ciśnienia ze zmianą temperatury.

Służą do pomiarów małych temperatur.

 Termorezysty - to elementy elektryczne, które mierzą zmiany temperatury poprzez pomiar związanej z nią zmiany oporu przewodnika bądź półprzewodnika.

 Termopary to układy dwóch przewodników, na stykach których wytwarza się napięcie termoelektryczne, proporcjonalne do różnicy temperatur obu styków.

 Pirometry mierzą temperaturę poprzez pomiar (porównanie) emisji promieniowania ciała, którego temperaturę chcemy określić, z emisją ciała doskonale czarnego - nadają się do pomiaru wysokich temperatur i do pomiarów „na odległość”.

 Bolometry również bazują na fakcie, że emisja promieniowania danego ciała jest proporcjonalna do jego temperatury.

 Układy bimetali służą raczej jako dwustanowe przełączniki termiczne, niż termometry, ale też pełnią rolę „mierników” temperatury.

 Budowa wszystkich tych urządzeń bazuje na zerowej zasadzie termodynamiki: jeżeli ciało 1 i ciało 2 znajdują się w równowadze termicznej i ciała 2 i 3 są również w takiej równowadze, to ciała 1 i 3 są także w tej samej równowadze termicznej w której byłyby, gdyby były w kontakcie ze sobą.

30.Ekwipartycji energii zasada, w termodynamice, twierdzenie mówiące, że w klasycznym układzie znajdującym się w równowadze termodynamicznej energia przypadająca na każdy translacyjny lub obrotowy stopień swobody równa jest kT/2, natomiast na stopień swobody związany z drganiem (w założeniu harmonicznym) przypada kT, gdzie k stała Boltzmanna, T - temperatura bezwzględna. Zasada ekwipartycji energii została zaproponowana przez Maxwella, który zauważył, że energia gazu jest wydzielana między ruch postępowy a obrotowy. Zasada ta jest zasadą termodynamiki, która głosi, że dostępna energia jaką dysponuje cząsteczka jest równo rozkładana pomiędzy wszystkie możliwe sposoby jej wykorzystania

Energia relatywistyczna (wiąże sięz ogólną teorią względności Einsteina. Zdefiniowana jest jako energia całkowita ciała izolowanego od otoczenia, a więc nie znajdującego się pod żadnym wpływem potencjałów zewnętrznych):

 Podana definicja pędu w przypadku prędkości dużo mniejszych od prędkości światła przechodzi w definicję klasyczną:

 Energia zdefiniowana przez Einsteina też powinna ulec takiej transformacji, a więc:

 Dla małych prędkości możemy jeszcze skorzystać z rozwinięcia w szereg wyrażenia na energię. Otrzymamy wtedy:

 Przypomnijmy wzór na rozwinięcie „nowej” definicji energii:

 Drugi człon jest klasyczną energią kinetyczną - energią cząstki swobodnej o prędkości . Pierwszy człon jest natomiast pewną stałą, którą według praw mechaniki klasycznej można dodać jako dowolną wartość do całkowitej energii ciała (por. pojęcie energii potencjalnej!).

 Według Einsteina ten drugi człon:

ma sens energii spoczynkowej ciała - wielkości, której istnieniu zawdzięczamy m.in. bombę atomową...

 Według przewidywań Einsteina, spoczywająca masa zawiera olbrzymią ilość energii:

Nawet zmniejszenie masy spoczynkowej cząstki (np. w wyniku rozpadu promieniotwórczego - tzw. defekt masy) o niewielką ilość spowodowałoby wyzwolenie potężnej energii.

Energia węgla:

1. spalonego klasycznie w elektrociepłowni:

2. uzyskana z wyzwolenia z masy spoczynkowej:

 Definicja energii kinetycznej: część energii całkowitej cząstki, wynikająca z ruchu cząstki (a więc związana z jego prędkością) - definicja prawdziwa zarówno w mechanice klasycznej, jak i relatywistycznej.

 W mechanice relatywistycznej możemy więc obliczyć energię kinetyczną jako różnicę między energią całkowitą a energią spoczynkową:

 Dla małych prędkości wykorzystujemy rozwinięcie dwumianu:

co daje nam ostatecznie znane wyrażenie:

 Korzystając z wprowadzonych definicji relatywistycznego pędu i energii (dla przypomnienia):

i

możemy znaleźć związki między pędem i energią w ujęciu relatywistycznym:

1. dzieląc stronami:

2. rugując z obu równań prędkość cząstki :

 Taka postać równań na pęd i energię implikuje jeszcze jeden ważny fakt - podstawowy dla mechaniki relatywistycznej: żadna cząstka materialna () nie może osiągnąć prędkości światła , gdyż wtedy jej pęd i energia wzrosłyby do nieskończoności.

Fala Elektromagnetyczna

Promieniowanie elektromagnetyczne (fala elektromagnetyczna) - rozchodzące się w przestrzeni zaburzenie pola elektromagnetycznego. Zaburzenie to ma charakter fali poprzecznej, w której składowa elektryczna i magnetyczna są prostopadłe do siebie, a obie są prostopadłe do kierunku rozchodzenia się promieniowania.

 Fale radiowe: - częstotliwości rzędu kiloherców i megaherców;

- długości rzędu kilometrów i metrów;

 Mikrofale: - częstotliwości rzędu gigaherców (10⁹ Hz);

- długości rzędu centymetrów i milimetrów;

 Podczerwień: - częstotliwości 10¹¹ do 10¹⁴ Hz;

- długości milimetrowe do mikrometrowych;

 Światło widzialne: - 400800 nm

 Ultrafiolet: - 10400 nm (nadfiolet)

 Promieniowanie rentgenowskie (X): - 0,00510 nm

 Promieniowanie gamma (): - długości poniżej 10^-12 m

Z równań Maxwella w przestrzeni nie zawierającej ładunków (w próżni) wynika:

gdzie

H - wektor natężenia pola magnetycznego,

E - wektor natężenia pola elektrycznego.

Równania te są liniowymi równaniami różniczkowymi fali rozchodzącej się z prędkością

gdzie: ε to przenikalność elektryczna, a μ to przenikalność magnetyczna ośrodka, w którym rozchodzi się fala. W próżni prędkość ta jest prędkością światła w próżni i określa ją wzór:

gdzie przenikalności z indeksem 0 odnoszą się do próżni. Rozwiązaniem różniczkowych równań Maxwella są równania fali biegnącej. Dla fali płaskiej rozchodzącej się w kierunku x równania te mają postać:

gdzie

E₀ - amplituda natężenia pola elektrycznego,

H₀ - amplituda natężenia pola magnetycznego,

ν - częstotliwość fali elektromagnetycznej,

λ - długość fali.

Równania Maxwella i ich rozwiązanie pozwoliło połączyć pole elektryczne i magnetyczne w jedno pole elektromagnetyczne i pokazało bezpośredni związek tego pola ze światłem.

Promieniowanie elektromagnetyczne, choć jest falą, jak wynika z równań Maxwella, jest równocześnie strumieniem kwantów - fotonów. Im mniejsza długość fali, tym bardziej ujawnia się cząsteczkowa natura promieniowania elektromagnetycznego. Energia kwantu zależy od długości fali zgodnie ze wzorem:

Zasada ekwipartycji energii

Zasada ekwipartycji energii została zaproponowana przez Maxwella, który zauważył, że energia gazu jest wydzielana między ruch postępowy a obrotowy. Zasada ta jest zasadą termodynamiki, która głosi, że dostępna energia jaką dysponuje cząsteczka jest równo rozkładana pomiędzy wszystkie możliwe sposoby jej wykorzystania

Zasada ekwipartycji energii - zasada termodynamiczna mówiąca (w oparciu o mechanikę statystyczną i przy założeniu obowiązywania mechaniki Newtona), że dostępna energia jaką dysponuje cząsteczka (np. gazu) rozkłada się "po równo" na wszelkie możliwe sposoby jej wykorzystania (tzw. stopnie swobody). Niezależnie od tego czy jest to stopień swobody związany z energią obrotu, ruchu postępowego czy związany z drganiami cząstek. Zgodnie z prawem średnia energia cząstki (energia o charakterze wewnętrznym - nie związana z ruchem całego układu) wynosi:

gdzie:

• 
  - temperatura układu w kelwinach,

• 
  - stała Boltzmanna,

• 
  - liczba stopni swobody cząsteczki:

• f = 3 dla cząsteczek jednoatomowych (np. gazy szlachetne)

• f = 3 + 2 + 2(3A − 5) = 6A − 5 dla cząsteczek liniowych, (kolejno: ruchy postępowe, ruchy obrotowe, drgania wewnątrz cząsteczki)

• f = 3 + 3 + 2(3A − 6) = 6A − 6 dla cząsteczek nieliniowych,

• f = 6 dla ciał stałych

• A - liczba atomów cząsteczki.

Średnią energię można pomnożyć przez liczbę cząsteczek i otrzymać energię wewnętrzną jednoatomowego gazu doskonałego:

• N - liczba cząsteczek w układzie,

• n - liczba moli cząstek w układzie,

• R - stała gazowa.

Lub też ogólnie:

---