MODEL EKONOMETRYCZNY

Badanie dotyczące kształtowania się przeciętnej ceny makaronu w latach 1990-2001.

Rok	Y	X1	X2	X3	X4	X5	X6
1990	0,52	0,34	0,11	1,56	65,5	8,462	585,8
1991	0,72	0,35	0,12	1,92	65,7	9,026	70,3
1992	1,07	0,68	0,13	2,04	69,5	9,27	43
1993	1,31	0,73	0,34	2,76	60	7,368	35,3
1994	1,81	0,85	0,28	2,88	67,6	8,243	32,2
1995	2,24	1,09	0,3	3,12	74	7,658	27,8
1996	1,4	1,49	0,31	3	105	8,668	19,9
1997	1,55	1,66	0,38	3,36	112	8,576	14,9
1998	1,7	1,6	0,3	3,72	119	8,193	11,8
1999	2,26	1,4	0,32	3,84	109	9,537	7,3
2000	3,46	1,77	0,36	4,32	102	9,051	10,1
2001	3,59	1,62	0,33	4,68	107	8,503	5,5
Suma	21,63	13,58	3,28	37,2	1056,3	102,555	863,9

Zmienna objaśniana:

Y - przeciętna cena makaronu (zł /0,5kg)

Zmienne objaśniające:

X₁ - przeciętna cena detaliczna mąki (zł/1kg)

X₂ - przeciętna cena detaliczna jajek (zł/szt.)

X₃ - przeciętne roczne spożycie makaronu na 1 osobę w gospodarstwie domowym (kg)

X₄ - wielkość produkcji makaronu (tys. t)

X₅ - zbiory pszenicy w roku poprzednim (mln t)

X₆ - inflacja (w %)

DOBÓR ZMIENNYCH DO MODELU

Na podstawie danych wyznaczamy wektor współczynników korelacji zmiennej objaśnianej Y z potencjalnymi zmiennymi objaśniającymi; X_1, X_2, X_3, X_4, X_5, X₆ ze wzoru:

=
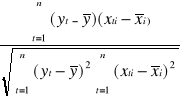
( i = 1,2,...,m)

Otrzymujemy wektor R₀

R_{0 =}

Obliczamy współczynniki korelacji między zmiennymi objaśniającymi X_1, X_2, X_3, X_4, X_5, X₆ według wzoru:

=
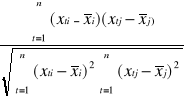
(i, j = 1,2,...,m)

Otrzymujemy macierz współczynników korelacji pomiędzy potencjalnymi zmiennymi objaśniającymi:

R =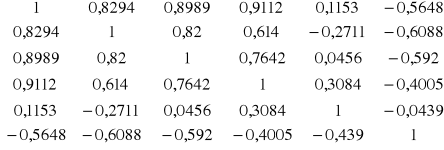

• Dobór zmiennych do modelu metodą analizy grafów.

Obliczamy wartość krytyczną współczynnika korelacji według wzoru:

r* =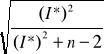

Dla poziomu istotności α=0,05 oraz dla n-2 stopni swobody, czyli 12-2=10 odczytujemy wartość krytyczną z tablic t-Studenta, która wynosi:

I*, czyli (t²_α ) = 2,228.

r* =
= 0,57596

Współczynniki korelacji spełniające relację: r
≤ r* dla i ≠ j, są statystycznie nieistotne i zastępuje je w macierzy R′ zerami.

R′ =

Na podstawie powyższej macierzy budujemy graf powiązań pomiędzy zmiennymi.

Zmienne objaśniające połączyły się w dwie grupy. Z grupy pierwszej wejdzie zmienna X₃, ponieważ jest silniej skorelowana ze zmienna endogeniczną niż X₂

oraz zmienna X₅, jako wierzchołek izolowany.

Model ma postać:

Y=α
+α
X
+α
X
+ε

ESTYMACJA PARAMETRÓW STRUKTURALNYCH MODELU

Wektor ocen parametrów strukturalnych modelu:

Y - wektor obserwacji zmiennej objaśnianej

Y=

X - wektor obserwacji zmiennych objaśniających

X=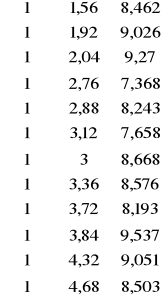

X^TX =

(X^TX)^-1 =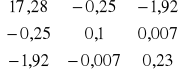

X^TY =

(X^TX)^-1X^TY =

Model po oszacowaniu parametrów strukturalnych ma postać:

Y = -1,3736+0,9246X
+0,0363X

• a₀ = -1,3736

Wartość parametru a₀ informuje o przeciętnej cenie makaronu, przy zerowym poziomie przeciętnego rocznego spożycia makaronu na 1 osobę w gospodarstwie domowym oraz przy zerowych zbiorach pszenicy w poprzednim roku.

• a₁= 0,9246

Jeżeli przeciętne roczne spożycie makaronu na 1 osobę w gospodarstwie domowym wzrośnie o 1 kg to spowoduje to wzrost przeciętnej ceny makaronu o 0,9246 zł(czyli o około 92 groszy), przy założeniu, że zbiory pszenicy z roku poprzedniego będą na stałym, niezmiennym poziomie.

• a₂ = 0,0363

Jeżeli zbiory pszenicy z roku poprzedniego wzrosną o 1 mln ton, to spowoduje to wzrost przeciętnej ceny makaronu o 0,0363 zł (czyli o około 4 grosze), przy założeniu, że przeciętne spożycie makaronu na 1 osobę w gospodarstwie domowym będzie utrzymywać się na stałym, niezmiennym poziomie.

WERYFIKACJA STATYSTYCZNA MODELU

Szacuję wariancję odchyleń na podstawie wzoru:

Y^TY = ∑ y² = 49,1633

a^T*X^TY=
*
=47,60863

S²_e=
(49,1633-47,60863)=
=0,1727

Odchylenie standardowe składnika losowego:

S_e=
=0,4156

Wartości empiryczne przeciętnej ceny makaronu różnią się średnio od wartości teoretycznych ceny przeciętnej makaronu wynikających z modelu o 0,4156 jednostki.

Macierz wariancji i kowariancji ocen parametrów strukturalnych modelu:

D²(a) = Se²(X^TX)^-1

D²(a) = 0,1727*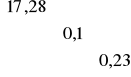
=

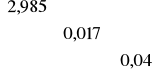
Standardowe błędy szacunku obliczamy ze wzoru: S(a_i)=

S(a₀) =
= 1,73

Parametr a₀ różni się średnio od parametru α₀ o +/- 1,73 jednostki.

S(a₁) =
= 0,13

Parametr a₁ różni się średnio od parametru α₁ o +/- 0,13 jednostki.

S(a₂) =
= 0,2

Parametr a₂ różni się średnio od parametru α₂ o +/- 0,2 jednostki.

Y = -1,3736+0,9246X
+0,0363X

(1,73) (0,13) (0,2)

WSPÓŁCZYNNIK ZBIEŻNOŚCI

^ 

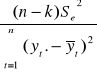
Y
0,52	-1,2825	1,6448
0,72	-1,0825	1,1718
1,07	0,7325	0,5366
1,31	-0,4925	0,2426
1,81	0,0075	0,00006
2,24	0,4375	0,1914
1,4	-0,4025	0,162
1,55	-0,2525	0,0638
1,7	-0,1025	0,0105
2,26	0,4547	0,2093
3,46	1,6575	2,7473
3,59	1,7875	3,1956
		10,1758

^ 
, (,

Współczynnik zbieżności mówi o tym, że 15,27% zmienności przeciętnej ceny makaronu nie zostało wyjaśnione przez model.

Współczynnik zbieżności przyjmuje wartości z przedziału [0;1].

Dopasowanie modelu do zmiennych jest tym lepsze, im współczynnik zbieżności jest bliższy zeru. Dopasowanie modelu w tym przypadku jest dobre.

WSPÓŁCZYNNIK DETERMINACJI

R² = 1 - ^

R² = 1 - 0,1527=0,8473 (84,73%)

Wyznaczony model w 84,73% wyjaśnia zmienność (kształtowanie się) przeciętnej ceny makaronu.

Współczynnik determinacji przyjmuje wartości z przedziału [0;1]. Dopasowanie modelu do zmiennych jest tym lepsze, im współczynnik zbieżności jest bliższy jedności . Dopasowanie modelu w tym przypadku jest dobre.

WSPÓŁCZYNNIK KORELACJI WIELORAKIEJ

R =

R =
=0,9205

Wynik ten oznacza, że występuje silna zależność liniowa między przeciętną ceną makaronu a przeciętnym rocznym spożyciem makaronu na 1 osobę w gospodarstwie domowym i zbiorami pszenicy w roku poprzednim. Tak więc dopasowanie modelu do danych empirycznych jest bardzo dobre.

WSPÓŁCZYNNIK ZMIENNOŚCI LOSOWEJ

V =
× 100%

=
=1,8025

V =
*100% = 9,58 %

Oznacza to, że odchylenie standardowe reszt stanowi 9,58% średniej arytmetycznej wartości przeciętnej ceny makaronu. Im mniejsza wartość tego wskaźnika, tym lepsze dopasowanie modelu do danych empirycznych. W tym przypadku można stwierdzić, że model jest dobrze dopasowany do danych empirycznych, ponieważ V_e < 10%.

BADANIE ISTOTNOŚCI PARAMETRÓW STRUKTURALNYCH

H₀ :α_i = 0

H₁ :α_i ≠ 0

│ a_i │

Postać statystyki testowej - ta_i =

S(a_i)

Z tablic testu t-Studenta dla przyjętego poziomu istotności α = 0,05; oraz dla n-k stopni swobody, czyli (12-3=9odczytuję wartość krytyczną t_α = 2,262.

H₀ :α₀ = 0

H₁ :α₀ ≠ 0

ta₀ =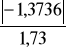
= 0,794

H₀ :α₁ = 0

H₁ :α₁ ≠ 0

ta₁ =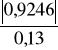
= 7,112

H₀ :α₂ = 0

H₁ :α₂ ≠ 0

ta₂ =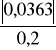
= 0,1815

• ta₀ < t_α i ta₂ < t_α

Na poziomie istotności α = 0,05 nie ma podstaw do odrzucenia hipotezy zerowej H₀. Zatem parametr strukturalny α₀ nieistotnie różni się od zera. Parametr strukturalny α₂ także nieistotnie różni się od zera, dlatego też zbiory pszenicy w roku poprzednim nie wpływają w istotny sposób na przeciętną cenę makaronu.

• ta₁> t_α

Na poziomie istotności α = 0,05 hipotezę zerową H₀ należy odrzucić na rzecz hipotezy alternatywnej H₁. Oznacza to, że parametr α₁ różni się w sposób istotny od zera, dlatego też przeciętne spożycie makaronu na 1 osobę w gospodarstwie domowym oddziałuje w sposób istotny na przeciętną cenę makaronu.

BADANIE WŁASNOŚCI ODCHYLEŃ LOSOWYCH

1. LOSOWOŚĆ

e =
-
=

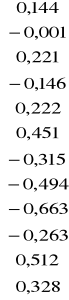
H₀: [Y = f(x₁...x_n)] - model _t jest losowy

H₁: [Y ≠ f(x₁...x_n)] - model _t nie jest losowy

a b a b a a b b b b a a

k_emp = 7 (serie)

n₁ = 6

n₂ = 6

Dla poziomu istotności γ= 0,05 oraz dla n₁i n₂ z tablic liczby serii odczytane są wartości krytyczne k₁ i k₂.

S₁* =
=0,025; n₁=6, n2=6 k₁ = 3

S₂* =1-
=0,975; n₁=6, n₂=6 k₂ = 10

S₁* < k_emp< S₂*, czyli 3<7<10

Na poziomie istotności γ= 0,05 nie ma podstaw do odrzucenia hipotezy zerowej oznacza to, że rozkład odchyleń losowych jest losowy, a więc postać analityczna modelu została dobrana prawidłowo.

2. BADANIE ISTOTNOŚCI WSPÓŁCZYNNIKA AUTOKORELACJI I RZĘDU.

_ ρ₁ = 0

H₁: ρ₁ ≠ 0

d =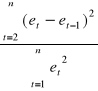

et

et-1

et-et-1

(et-et-1)^2

et^2

0,144				0,020736
-0,001	0,144	-0,145	0,021025	0,000001
0,221	-0,001	0,222	0,049284	0,048841
-0,146	0,221	-0,367	0,134689	0,021316
0,222	-0,146	0,368	0,135424	0,049284
0,451	0,222	0,229	0,052441	0,203401
-0,315	0,451	-0,766	0,586756	0,099225
-0,494	-0,315	-0,179	0,032041	0,244036
-0,663	-0,494	-0,169	0,028561	0,439569
-0,263	-0,663	0,4	0,16	0,069169
0,512	-0,263	0,775	0,600625	0,262144
0,328	0,512	-0,184	0,033856	0,107584
SUMA			1,834702	1,565306

d =
= 1,1721

X₅

X₁

X₄

X₆

X₂

X₃

---