1. Przyjęcie geometrii stropu
1.1 Rozstaw żeber stropowych
Żebra stropowe rozmieszczone są w kierunku poprzecznym w odległości 1,70 m miedzy sobą.
1.2. Przyjęcie grubości i rodzaju płyty stropowej
Strop składa się z płyty żelbetowej grubości 10 cm, jednej warstwy papy, warstwy wyrównawczej i tynku grubości 1,5cm oraz lastryka grubości 2cm
2. Obliczenie żebra stropowego
Schemat statyczny żebra stropowego stanowi belka jednoprzęsłowa o rozpiętości obliczeniowej: lż = 5,2 · 1,025 = 5,33 [m]:
2.1. Zestawienie obciążeń na żebro:
Lp. |
Rodzaj obciążenia |
Obc. charakterystyczne [kN/m] |
γƒ |
Obc. obliczeniowe [kN/m] |
1. |
Lastryko 0,02 · 22 · 1,7 |
0,748 |
1,3 |
0,972 |
2+4. |
W-wa wyrównawcza 0,015 · 21 · 1,7 · 2 |
1,071 |
1,3 |
1,392 |
3. |
Papa x1 0,002 · 1,7 |
0,003 |
1,2 |
0,004 |
5. |
Płyta żelbetowa 0,1 · 25 · 1,7 |
4.250 |
1,1 |
4,675 |
6. |
Tynk 0,015 · 19 · 1,7 |
0,485 |
1,3 |
0,582 |
7. |
Ciężar własny belki I260 |
0,419 |
1,1 |
0,461 |
Obciążenie stałe (użytkowe) gż |
6,976 |
|
8,086 |
|
Obciążenie zmienne pż |
6,2 · 1,7 = 10,540 |
1,2 |
12,648 |
|
Obciązenie całkowite |
gż + pż = 17,516 |
|
gż + pż = 20,734 |
|
2.2. Statyka żebra
Rż ![]()
TA = 55,256 kN
TB = -55,256 kN
Mmax = ![]()
Wykres sił tnących
Wykres momentów zginających
2.3. Przyjęcie przekroju żebra
Wstępne przyjęcie przekroju ze stali St3SX o fd = 215 [MPa] = 21,5 [kN/cm²]
Obciążenie działa statycznie, a przekrój jest klasy 1. ![]()
αp = 1,07
W ![]()
W![]()
Wx dla I260 = 442 cm³
Sprawdzenie klasy przekroju
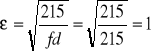
dla środnika
![]()
dla pasa
![]()
Ponieważ warunki smukłości zostały spełnione możemy przekrój zaliczyć do klasy 1.
2.4. Sprawdzenie warunków obliczeniowych
Sprawdzenie warunku nośności przekroju klasy 1 na zginanie:
Element zabezpieczony jest przed zwichrzeniem, czyli ![]()
L = 1
MR = ![]()
MR = ![]()
Sprawdzenie warunku nośności:
![]()
<1
![]()
Warunek nośności jest spełniony.
Sprawdzenie warunku smukłości przy ścinaniu dla środnika:
![]()
Sprawdzenie warunku nośności przekroju na ścinanie:
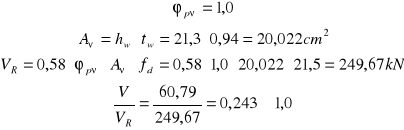
Warunek nośności jest spełniony.
3. Podciąg
3.1. Obliczenie żebra stropowego
Schemat statyczny podciągu stropowego stanowi belka jednoprzęsłowa o rozpiętości obliczeniowej: lp = 6 · 1,65 = 9,9 [m]:
3.2. Zestawienie obciążeń na podciąg:
Lp. |
Rodzaj obciążenia |
Obc. charakterystyczne [kN/m] |
γƒ |
Obc. obliczeniowe [kN/m] |
1. |
Ciężar własny podciągu 2I500 2 · 1,41 |
2,820 |
1,1 |
3,102 |
2. |
Ciężar ściany działowej 0,38 · 3,5 · 18 |
23,940 |
1,1 |
26,334 |
3. |
Obustronny tynk 2 · 0,015 · 3,5 · 19 |
1,995 |
1,3 |
2,594 |
Obciążenie równomiernie rozłożone |
28,755 |
|
32,030 |
|
Obciążenie skupione od żeber Pż = 2Rż |
110,512 |
|
110,512 |
|
3.3. Statyka podciągu
![]()
![]()


3.4. Przyjęcie przekroju poprzecznego podciągu w formie blachownicy spawanej÷
Przyjęcie przekroju ze stali 18G2A o ![]()
ZAŁOŻENIA:
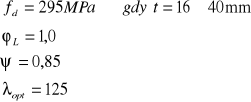
![]()
przyjęto 5040 cm³
Przyjęcie wymiarów środnika:
- wysokość środnika
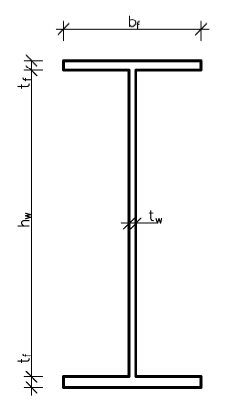
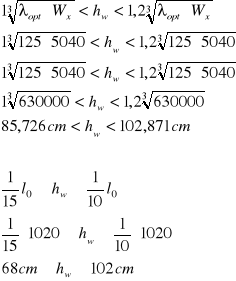
Przyjęto ![]()
- grubość środnika
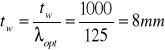
Przyjęto ![]()
Przyjęcie wymiarów pasów:
- szerokość pasów
![]()
- grubość pasów
![]()
Przyjęto ![]()
Obliczanie momentu bezwładności
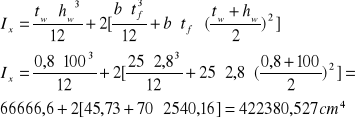
Obliczanie pola przekroju
![]()
Obliczanie wskaźnika zginania
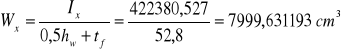
Obliczanie promienia bezwładności
![]()
Sprawdzenie klasy przekroju
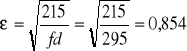
dla środnika
![]()
KLASA 4
dla pasa
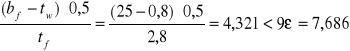
KLASA 1
Przekrój klasy 4.
3.5. Sprawdzenie warunków obliczeniowych
Sprawdzenie warunku nośności przekroju klasy 4 na zginanie:
Rozstaw żeberek usztywniających a = 1,70 [m] = 170[cm]

Sprawdzenie stanu granicznego nośności na ścinanie
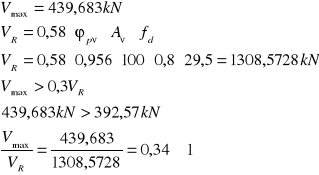
Moment bezwładności części przekroju czynnej przy ścinaniu

![]()
Warunek nośności został spełniony
3.6. Połączenie środnika blachownicy z pasami
Przyjęcie grubości spoiny
![]()
Przyjęto ![]()
Spoina obciążona siłą V=439,683kN![]()
Moment statyczny pasa względem osi obojętnej
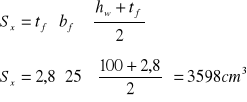
Grubość spoin
![]()
Nośność spoiny
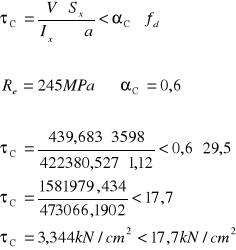
Warunek nośności spoin został spełniony
3.7. Pośrednie żebra usztywniające
Przyjęto żebra usztywniające grubości ![]()
Szerokość żebra:
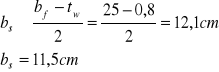
Warunek sztywności:
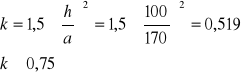
Przyjęto k=0,75
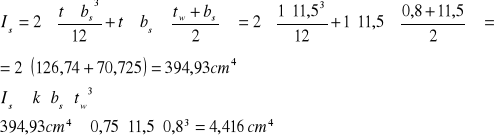
Warunek sztywności został spełniony
![]()
klasa 3.
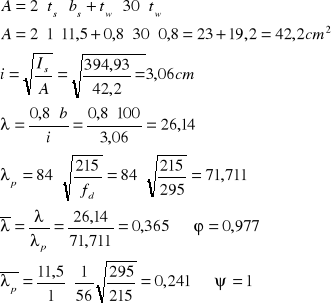
Nośność żebra usztywniającego
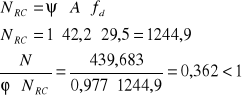
Warunek nośności został spełniony
1

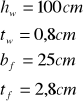
Wyszukiwarka
Podobne podstrony:
Projekt Konstytucji według PiS ćwiczenie intelektualne
projekt konstytucji IV RP
s michalkiewicz projekt konstytucji rp
Kamil Piskała, Polscy socjaliści wobec projektu konstytucji BBWR z lutego 1929 r
konstytucja z 1997 projekt zmiany
Projekt nowej konstytucji iraku 28 sierpnia 2005
Konstytucja RP Projekt Stanisława Michalkiewicza
konstytucja z 1997 projekt zmiany
Michalkiewicz Konstytucja Rzeczypospolitej Polskiej (projekt)
projekt o narkomanii(1)
!!! ETAPY CYKLU PROJEKTU !!!id 455 ppt
Wykład 3 Dokumentacja projektowa i STWiOR
Projekt nr 1piątek
Projet metoda projektu
więcej podobnych podstron