PRACA PRZEJ SCIOWA
EKONOMETRII
TEMAT
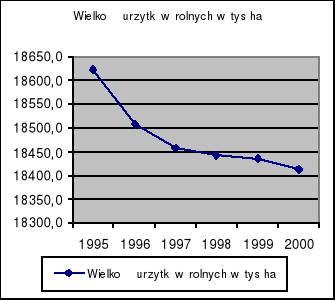
ESTYMACJA PARAMETRÓW MODELU DYNAMIKI ROZWOJOWEJ SZTAŁTOWANIA SIĘ WIELKOŚCI URZYTKÓW ROLNYCH W POLSCE.
1. Specyfikacja zmiennych objaśnianych zmiennych objaśniających.
l.p |
lata |
Wydobycie ropy [tys. ha] |
1 |
1995 |
18622,3 |
2 |
1996 |
18508,2 |
3 |
1997 |
18457,0 |
4 |
1998 |
18442,7 |
5 |
1999 |
18434,7 |
6 |
2000 |
18413,2 |
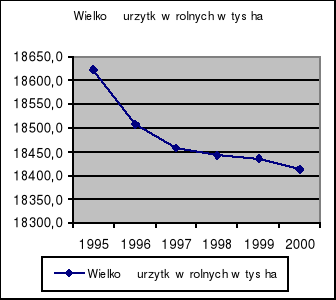
Celem niniejszej pracy jest opracowanie modelu dynamiki rozwojowej kształtowania się wielkości użytków rolnych w Polsce. Zmienną objaśnianą jest wielkość użytków rolnych, natomiast zmienną objaśniającą jest zmienna okresowa t przyjmująca wartości od 1 do 6 - t = 1...n, gdzie n jest liczą obserwacji
2 Estymacja parametrów strukturalnych modeli dynamiki rozwojowej trendu linowego logarytmicznego, potęgowego oraz wykładniczego.
Model liniowy
PODSUMOWANIE - WYJŚCIE |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Statystyki regresji |
|
|
|
|
|
|
|
|
Wielokrotność R |
0,891271 |
|
|
|
|
|
|
|
R kwadrat |
0,794364 |
|
|
|
|
|
|
|
Dopasowany R kwadrat |
0,742955 |
|
|
|
|
|
|
|
Błąd standardowy |
38,92898 |
|
|
|
|
|
|
|
Obserwacje |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ANALIZA WARIANCJI |
|
|
|
|
|
|
||
|
df |
SS |
MS |
F |
Istotność F |
|
|
|
Regresja |
1 |
23416,69 |
23416,69 |
15,45181 |
0,01709 |
|
|
|
Resztkowy |
4 |
6061,861 |
1515,465 |
|
|
|
|
|
Razem |
5 |
29478,55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Współczynniki |
Błąd standardowy |
t Stat |
Wartość-p |
Dolne 95% |
Górne 95% |
Dolne 95,0% |
Górne 95,0% |
Przecięcie |
18607,71 |
36,24091 |
513,445 |
8,63E-11 |
18507,09 |
18708,33 |
18507,09 |
18708,33 |
Zmienna X 1 |
-36,58 |
9,305806 |
-3,93088 |
0,01709 |
-62,4171 |
-10,7429 |
-62,4171 |
-10,7429 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SKŁADNIKI RESZTOWE - WYJŚCIE |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Obserwacja |
Przewidywane Y |
Składniki resztowe |
|
|
|
|
|
|
1 |
18571,13 |
51,16667 |
|
|
|
|
|
|
2 |
18534,55 |
-26,3533 |
|
|
|
|
|
|
3 |
18497,97 |
-40,9733 |
|
|
|
|
|
|
4 |
18461,39 |
-18,6933 |
|
|
|
|
|
|
5 |
18424,81 |
9,886667 |
|
|
|
|
|
|
6 |
18388,23 |
24,96667 |
|
|
|
|
|
|
y = 108607,71 - 36,58 t
(36,241) (9,306)
R2 = 79,44 %
Se = 38,929
![]()
= 18479,68
Vs = 0,21 %
Model logarytmiczny
PODSUMOWANIE - WYJŚCIE |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Statystyki regresji |
|
|
|
|
|
|
|
|
Wielokrotność R |
0,97462 |
|
|
|
|
|
|
|
R kwadrat |
0,949884 |
|
|
|
|
|
|
|
Dopasowany R kwadrat |
0,937354 |
|
|
|
|
|
|
|
Błąd standardowy |
19,21822 |
|
|
|
|
|
|
|
Obserwacje |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ANALIZA WARIANCJI |
|
|
|
|
|
|
||
|
df |
SS |
MS |
F |
Istotność F |
|
|
|
Regresja |
1 |
28001,19 |
28001,19 |
75,81411 |
0,000958 |
|
|
|
Resztkowy |
4 |
1477,36 |
369,3401 |
|
|
|
|
|
Razem |
5 |
29478,55 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Współczynniki |
Błąd standardowy |
t Stat |
Wartość-p |
Dolne 95% |
Górne 95% |
Dolne 95,0% |
Górne 95,0% |
Przecięcie |
18603,52 |
16,24296 |
1145,328 |
3,49E-12 |
18558,42 |
18648,62 |
18558,42 |
18648,62 |
Zmienna X 1 |
-112,934 |
12,97025 |
-8,70713 |
0,000958 |
-148,945 |
-76,9224 |
-148,945 |
-76,9224 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SKŁADNIKI RESZTOWE - WYJŚCIE |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Obserwacja |
Przewidywane Y |
Składniki resztowe |
|
|
|
|
|
|
1 |
18603,52 |
18,78021 |
|
|
|
|
|
|
2 |
18525,24 |
-17,0402 |
|
|
|
|
|
|
3 |
18479,45 |
-22,4495 |
|
|
|
|
|
|
4 |
18446,96 |
-4,26053 |
|
|
|
|
|
|
5 |
18421,76 |
12,93988 |
|
|
|
|
|
|
6 |
18401,17 |
12,03011 |
|
|
|
|
|
|
y = 18603,52 - 112,934 ln t
(16,243) (12,97)
R2 = 94,99 %
Se = 19,218
![]()
= 18479,68
Vs = 0,10 %
Model potęgowy
PODSUMOWANIE - WYJŚCIE |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Statystyki regresji |
|
|
|
|
|
|
|
|
Wielokrotność R |
0,974907 |
|
|
|
|
|
|
|
R kwadrat |
0,950443 |
|
|
|
|
|
|
|
Dopasowany R kwadrat |
0,938053 |
|
|
|
|
|
|
|
Błąd standardowy |
0,001032 |
|
|
|
|
|
|
|
Obserwacje |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ANALIZA WARIANCJI |
|
|
|
|
|
|
||
|
df |
SS |
MS |
F |
Istotność F |
|
|
|
Regresja |
1 |
8,17E-05 |
8,17E-05 |
76,71463 |
0,000937 |
|
|
|
Resztkowy |
4 |
4,26E-06 |
1,06E-06 |
|
|
|
|
|
Razem |
5 |
8,59E-05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Współczynniki |
Błąd standardowy |
t Stat |
Wartość-p |
Dolne 95% |
Górne 95% |
Dolne 95,0% |
Górne 95,0% |
Przecięcie |
9,831108 |
0,000872 |
11273,26 |
3,71E-16 |
9,828687 |
9,833529 |
9,828687 |
9,833529 |
Zmienna X 1 |
-0,0061 |
0,000696 |
-8,75869 |
0,000937 |
-0,00803 |
-0,00417 |
-0,00803 |
-0,00417 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SKŁADNIKI RESZTOWE - WYJŚCIE |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Obserwacja |
Przewidywane Y |
Składniki resztowe |
|
|
|
|
|
|
1 |
9,831108 |
0,001007 |
|
|
|
|
|
|
2 |
9,82688 |
-0,00091 |
|
|
|
|
|
|
3 |
9,824407 |
-0,00121 |
|
|
|
|
|
|
4 |
9,822653 |
-0,00023 |
|
|
|
|
|
|
5 |
9,821292 |
0,000698 |
|
|
|
|
|
|
6 |
9,82018 |
0,000643 |
|
|
|
|
|
|
ln y = 9,831 - 0,0061ln t
(0,0009) (0,0007)
R2 = 95,04 %
Se = 0,001
(ln y)śr= 9,82442
Vs = 0,01 %
MODEL WYKŁADNICZY
PODSUMOWANIE - WYJŚCIE |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
Statystyki regresji |
|
|
|
|
|
|
|
|
Wielokrotność R |
0,891881 |
|
|
|
|
|
|
|
R kwadrat |
0,795451 |
|
|
|
|
|
|
|
Dopasowany R kwadrat |
0,744314 |
|
|
|
|
|
|
|
Błąd standardowy |
0,002096 |
|
|
|
|
|
|
|
Obserwacje |
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ANALIZA WARIANCJI |
|
|
|
|
|
|
||
|
df |
SS |
MS |
F |
Istotność F |
|
|
|
Regresja |
1 |
6,84E-05 |
6,84E-05 |
15,55524 |
0,016903 |
|
|
|
Resztkowy |
4 |
1,76E-05 |
4,39E-06 |
|
|
|
|
|
Razem |
5 |
8,59E-05 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Współczynniki |
Błąd standardowy |
t Stat |
Wartość-p |
Dolne 95% |
Górne 95% |
Dolne 95,0% |
Górne 95,0% |
Przecięcie |
9,831337 |
0,001952 |
5037,803 |
9,32E-15 |
9,825919 |
9,836756 |
9,825919 |
9,836756 |
Zmienna X 1 |
-0,00198 |
0,000501 |
-3,94401 |
0,016903 |
-0,00337 |
-0,00059 |
-0,00337 |
-0,00059 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
SKŁADNIKI RESZTOWE - WYJŚCIE |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
Obserwacja |
Przewidywane Y |
Składniki resztowe |
|
|
|
|
|
|
1 |
9,829361 |
0,002754 |
|
|
|
|
|
|
2 |
9,827385 |
-0,00142 |
|
|
|
|
|
|
3 |
9,825408 |
-0,00221 |
|
|
|
|
|
|
4 |
9,823432 |
-0,00101 |
|
|
|
|
|
|
5 |
9,821456 |
0,000535 |
|
|
|
|
|
|
6 |
9,819479 |
0,001344 |
|
|
|
|
|
|
ln y = 9,831 - 0,002 t
(0,002) (0,0005)
R2 = 79,54 %
Se = 0,0021
(ln y)śr= 9,82442
Vs = 0,02 %
3 Wybór postaci analitycznej modelu.
Najlepiej dopasowanym modelem do danych empirycznych jest model potęgowy ponieważ charakteryzuje się najwyższym współczynnikiem determinacji R2
4 Interpretacja modelu
ln y = 9,831 - 0,0061ln t
(0,0009) (0,0007)
R2 = 95,04 %
Se = 0,001
(ln y)śr= 9,82442
Vs = 0,01 %
Trend: y = 18603,56.t-0,0061
R2 = 95,04 % - zmienność wielkości użytków rolnych została wyjaśniona przez model w 95,04 %.
Se = 0,001 - wartości zlogarytmowane teoretyczne różnią się od wartości zlogarytmowanych empirycznych średnio o ± 0,001 tys. ha.
Vs = 0,01 % - wielkość odchylenia standardowego Se wynosiła 0,01 % poziomu średniej arytmetycznej z logarytmów wielkości zmiennej y.
α0 = 18603,56 - teoretyczna wartość zmiennej objaśnianej w pierwszym roku obserwacji kształtowała się na poziomie 18603,56 tys. ha
α1 = -0,0061- nie interpretujemy.
Model jest dobrze dopasowany do danych empirycznych ponieważ R2 > 90 % oraz Vs < 10 % i może być podstawą prognozy badanego zjawiska do celów statystycznych.
5. Weryfikacja modelu
n= 6 - liczba obserwacji.
k= 1 - liczba zmiennych objaśniających.
α= 0,05
5.1. Istotności parametrów strukturalnych.
Hipotezy: H0 : [α=0] - parametry modelu nie są istotne,
H1 : [α≠0] - parametry modelu są istotne
Wartość testu t - Studenta - t*= t(α, n-k-1) = t*= t(0,05;4) = 2,776
ti = |αi |:Dαi
to = |9,831|: 0,00087 = 11273,26
t1 = |-0,0061|: 0,0007 = 8,759
ti > t* Parametry strukturalne modelu są istotne.
5.2. Losowości reszt.
Hipotezy: H0 : [y= α0 +α1t] - reszty modelu mają charakter losowy.
H1 : [y≠ α0 +α1t] - reszty modelu nie mają charaktery losowego
Reszty:
0,001007 |
-0,00091 |
-0,00121 |
-0,00023 |
0,000698 |
0,000643 |
S =3 - liczba serii; n1 = 3 - liczba reszt dodatnich, n2 = 3 - liczba reszt ujemnych.
Wartość testu: s* = s(α; n1; n2)= s(0,05;3;3) = 1
S> s* - reszty modelu mają charakter losowy.
5.3. Występowanie autokorelacji składników losowych.
Hipotezy: H0 : [ρ=0] - nie występuje autokorelacja odchyleń losowych.
H1 : [ρ≠0] - występuje autokorelacja odchyleń losowych.
Reszty |
et2 |
(et - et-1)2 |
0,001007 |
0,00000101 |
|
-0,00091 |
0,00000083 |
0,000003680 |
-0,00121 |
0,00000146 |
0,000000088 |
-0,00023 |
0,00000005 |
0,000000960 |
0,000698 |
0,00000049 |
0,000000860 |
0,000643 |
0,00000041 |
0,000000003 |
|
0,00000426 |
0,00000559 |
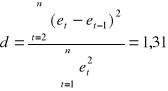
Wartości testu: dl = 0,610; du = 1,400
dl < < du - nie można podjąć decyzji.
5.4. Test Shapiro - Wilka - badanie charakteru rozkładu.
|
|
ai:n |
|
ei2 eśr = 0 |
-0,00121 |
0,00221540 |
0,6431 |
0,001425 |
0,00000146 |
-0,00091 |
0,00160955 |
0,2806 |
0,000452 |
0,00000083 |
-0,00023 |
0,00087219 |
0,0875 |
0,000076 |
0,00000005 |
0,000643 |
|
|
|
0,00000041 |
0,000698 |
|
|
|
0,00000049 |
0,001007 |
|
|
|
0,00000101 |
|
|
|
0,001953 |
0,00000426 |
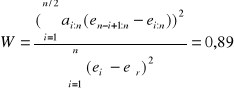
Wartość testu: W*(0,05; 6) = 0,788
W* < - rozkład ma charakter rozkładu normalnego.
6. Prognozowanie.
Prognoza punktowa na rok 2003 (okres T =9):
ln y = 9,831 - 0,0061 ln 9 = 9,82;
Wartość odlogartytmowana: y = 18353,89
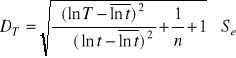
Średni błąd prognozy.
(ln t)śr= 1,096;
![]()
= 2,195;
![]()
= 0,001;
DT = 0,0013. Wartość odlogarytmowana: 1,001
Prognoza przedziałowa:
t (0,05; 4) = 2,776
![]()
= 9,814 wartość odlogarytmowana: 18287,21
![]()
= 9,821 wartość odlogarytmowana: 18420,82
Teoretyczna wartość kształtowania wielkości użytków rolnych w roku 2003 powinna wynosiła 18353,89 tys. ha. Wartość ta powinna różnić się od wartości rzeczywistej o +/- 1,001 tys. ha. Przedział ufności dla wartości prognozowanej zawiera się w granicach od 18287,21 do 18420,82 tys. ha.
14
Szukasz gotowej pracy ?
To pewna droga do poważnych kłopotów.
Plagiat jest przestępstwem !
Nie ryzykuj ! Nie warto !
Powierz swoje sprawy profesjonalistom.
![]()
![]()
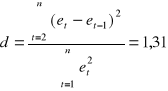
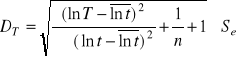
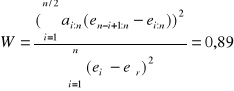
Wyszukiwarka
Podobne podstrony:
praca-magisterska-wa-c-7459, Dokumenty(2)
praca-magisterska-wa-c-7525, Dokumenty(2)
praca-magisterska-wa-c-7468, Dokumenty(2)
praca-magisterska-wa-c-7499, Dokumenty(2)
praca-magisterska-wa-c-7474, Dokumenty(2)
praca-magisterska-wa-c-7486, Dokumenty(2)
praca-magisterska-wa-c-7565, Dokumenty(2)
praca-magisterska-wa-c-7520, Dokumenty(2)
praca-magisterska-wa-c-8169, Dokumenty(2)
praca-magisterska-wa-c-7507, Dokumenty(2)
praca-magisterska-wa-c-7446, Dokumenty(2)
praca-magisterska-wa-c-7839, Dokumenty(2)
praca-magisterska-wa-c-8167, Dokumenty(2)
praca-magisterska-wa-c-7894, Dokumenty(2)
praca-magisterska-wa-c-7476, Dokumenty(2)
więcej podobnych podstron