Światło niespolaryzowane i macierz gęstości

Średnia wartość operatora
dla światła niespolaryzowanego

Jak dotąd rozpatrywaliśmy fotony w określonych stanach polaryzacji. Wyobraźmy sobie inną sytuację: wiązka monochromatyczna składa się z fotonów pochodzących z dwu różnych źródeł: jedno daje fotony w stanie
, druga w stanie
(gdzie
=0,

) [1,2]. Źródła wypromieniowują fotony zupełnie przypadkowo, są niezależne i w żaden sposób nie możemy przewidzieć z którego źródła fotony pochodzą. Przyjmijmy, że znamy stosunek natężeń źródeł - wagę wkładu każdego ze źródeł. Niech waga pierwszego układu będzie równa
, a drugiego
. Suma wag spełnia oczywisty warunek

. (9.1)

Znajdziemy wartość średnią wartość operatora
dla takiej wiązki. Przypomnijmy, że zgodnie ze wzorem (8.9) w przypadku fotonów w stanie
średnia wartość
jest równa

.

Teraz mamy do czynienia z dwoma źródłami wypromieniowującymi fotony z różnymi wagami, a więc i ze średnią ważoną

. (9.2)

Stwierdzenie: foton może być w stanie
lub
z prawdopodobieństwem odpowiednio
i
różni się od stwierdzenia: foton jest w stanie kwantowym będącym superpozycją stanów
Przedstawimy wektor stanu
w postaci superpozycji wektorów stanu

,

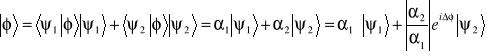
gdzie
,
. Jak widać, aby jednoznacznie określić liniową superpozycje stanów kwantowych, trzeba zadać różnicę faz
. Natomiast prawdopodobieństwo jest wielkością rzeczywistą, a więc gdy mówimy, że foton z prawdopodobieństwem
jest w stanie kwantowym
i z prawdopodobieństwem
w stanie
, to rozpatrujemy kom­bina­cję liniową tych stanów ze współczynnikami rzeczywistymi, które w żaden sposób nie są związane z amplitudami prawdopodobieństwa. Wynikają z mechanizmów wypromieniowania fotonów przez źródła światła, np. żarówki. Oczywiście najczęściej aby wyliczyć te prawdo­po­dobieństwa trzeba stosować metody kwantowej fizyki statystycznej.

Będziemy mówili o stanach czystych w przypadku układów znajdujących się w określonych stanach kwantowych. By określić wynik doświadczenia przeprowadzonego nad układem w czystym stanie kwantowym należy obliczyć amplitudę prawdopodobieństwa, a następnie prawdopodobieństwo. Gdy układ może znajdować się w kilku stanach kwantowych z pewnymi prawdopodobieństwami będziemy mówili o stanie mieszanym. By zadać stan mie­szany należy dopuszczalne stany, w których może znaleźć się układ i określić prawdopodobieństwa znalezienia się układu w każdym z tych dopuszczalnych stanów.

Zauważymy, że gdy w stanie kwantowym
określamy różnicę faz z błędem 2π, to rezultat obliczenia prawdopodobieństwa jest taki, jakbyśmy mieli do czynienia z stanem mieszanym. Wtedy dla fotonu w stanie
liczbę
można uważać za prawdopodobieństwo znalezienia fotonu w stanie
, natomiast
za prawdopodo­bień­stwo znalezienia go w stanie
. Sprawdzimy, że wzór (8.9) po uśrednieniu (8.13) po wszystkich dopuszczalnych fazach prowadzi do wzoru (9.2)

.

Po wymnożeniu czynników otrzymujemy

.

Lecz
. Jeżeli różnica faz
nie jest ustalona, to wynik wielu pomiarów otrzymamy uśredniając po różnicy faz. Zgodnie ze wzorem (8.12) odpowiednia średnia wartość, którą oznaczymy przy pomocy kreski nad wielkością uśrednianą, znika. Zatem

, (9.3a)

gdzie
. Liczby
spełniają warunek (9.1)

.

Ponieważ
jest dowolną parą wektorów ortogonalnych więc
i

. (9.3b)

Wynika stąd następujące określenie światła niespolaryzowanego: fotony całkowicie niespola­ryzowanej wiązki światła jednakowym prawdopodobieństwem mogą znajdować się w każdym z dwóch ortogonalnych stanów polaryzacji.

Pokażemy, że dla światła całkowicie niespolaryzowanego średnia wartość operatora nie zależy od wyboru bazy. W tym celu obliczymy średnią wartość jakiegoś operatora, np.

dla światła niespolaryzowanego. Niech
będą dowolnymi ortogonalnymi, unormowanymi do jedności wektorami stanu

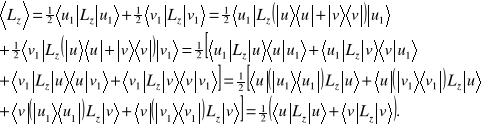
Ostatecznie

. (9.3c)

Wektory
są parą dowolnych, ortogonalnych wektorów unormowanych do jedności. Stwierdzamy więc, że światło jest całkowicie niespolaryzowane jeżeli z jednakowym prawdopodobieństwem jej fotony mogą być w każdym stanie polaryzacji.

9.2 Macierz gęstości i jej podstawowe własności

Dla światła niespolaryzowanego wprowadzimy operator statystyczny

. (9.4)

Ten operator nazywany jest także macierzą gęstości. Wzór (9.4) ma postać rozkładu spektralnego (§ 6.4).

Ponieważ iloczyny zewnętrzne
(i=1,2) są operatorami hermitowskimi, a prawdopodo­bieństwa p_i są liczbami rzeczywistymi więc operator statystyczny jest hermitowski

, (9.5a)

a więc jego elementy macierzowe spełniają warunek

. (9.5b)

Obliczymy ślad operatora statystycznego. Ponieważ ślad operatora nie zależy od wyboru bazy więc obliczymy go w jakiejś dowolnie wybranej bazie
. Po wykorzystaniu wzorów (9.4) i (7.18a) otrzymamy

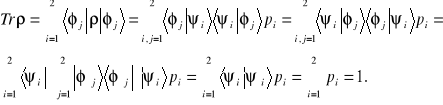
(9.6a)

Powyższy wzór jest słuszny nie tylko dla stanów polaryzacji fotonu. Dlatego zapiszemy go dla układu, którego bazy liczą s niezależnych liniowo wektorów

. (9.6b)

Zapiszemy wyrażenie (9.2) dla średniej wartości operatora
w stanie mieszanym w taki sposób, aby wyrażała się ona przez operator gęstości. Wstawimy z lewej i prawej strony operatora
dwie jedynki operatorowe (7.18a) i wykorzystamy definicję operatora staty­s­ty­cz­ne­go. Dokonamy także kilku prostych przekształceń

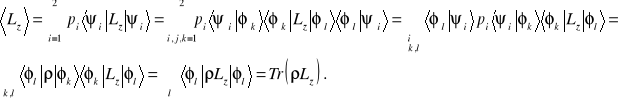
Powyższa relacja jest słuszna nie tylko dla stanów polaryzacji fotonów, dlatego zapiszemy ją dla dowolnego operatora
określającego własności jakiegoś układu, którego bazy liczą s unormowanych do jedności wektorów

. (9.7)

Oczywiście własność (9.6a) wynika także ze wzoru (9.7). Aby udowodnić to stwierdzenie rozpatrzymy średnią wartość operatora jednostkowego
i wykorzystamy wzór (9.4)

.

Przypomnijmy najważniejsze własności śladu. Chociaż operatory na ogół nie komu­tu­ją, to jednak można je pod znakiem śladu przestawiać. Niech
będą dwoma nie komutującymi operatorami (
) działającymi w przestrzeni wektorów stanu polaryzacji fotonu, mamy

. (9.8a)

Udowodnimy tę własność

.

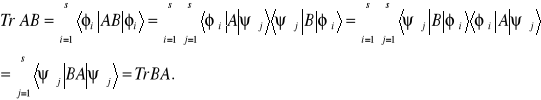
Pokażemy, że ślad nie zależy od wyboru bazy. Niech
będzie operatorem, zaś
,...,
będą dwoma wektorami bazy. Postępując podobnie jak w przypadku wyprowadzenia wzorów (9.5), (9.6) otrzymamy

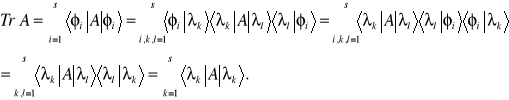
(9.8b)

Ponieważ ze zmianą bazy związane jest przekształceniem podobieństwa (7.26) po­wyż­sza własność wynika z własności (9.8a). Wybierzemy jakąś bazę, w której operator
reprezentuje macierz A. Niech
będzie macierzą unitarną (
). Rozpatrzymy ślad macierzy
. Przestawiając macierze
,
otrzymamy

.

Obliczymy ślad operatora statystycznego w dowolnej bazie

.

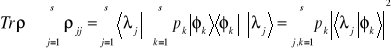
Jak widać elementy diagonalne macierzy gęstości
są nieujemne

. (9.9)

To stwierdzenie jest prawdziwe dla każdego wyboru bazy. Macierze o tej własności nazywamy nieujemnymi. Operator, który jest reprezentowany przez macierze nieujemne nazywamy operatorem nieujemnym. Macierz gęstości jest operatorem nieujemnym. W bazie wektorów własnych operator statystyczny ma postać macierzy diagonalnej, której wyrazy są równe prawdopodobieństwom p_i (i=1,...,s), pozostałe, niediagonalne wyrazy znikają. Ponieważ w dowolnej bazie suma wyrazów diagonalnych operatora statystycznego spełnia warunek (9.6b) więc jego diagonalne elementy macierzowe spełniają podwójną nierówność

. (9.10)

W bazie, w której operator statystyczny jest diagonalny spełniona jest nierówność

.

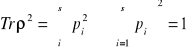
Lecz przekształcenie podobieństwa nie zmienia śladu, a więc otrzymujemy ogólną nierówność

. (9.11a)

Operator statystyczny jest hermitowski,
, zatem nierówność (9.11a) można zapisać inaczej

. (9.11b)

Warunek (9.11b) w istotny sposób ogranicza elementy macierzowe operatora statystycznego.

Zastanówmy się nad liczbą niezależnych parametrów, od których zależy macierz gęstości. Niech s będzie całkowitą liczbą jej wartości własnych. To oznacza, że macierz ją reprezentujące mają s kolumn i s wierszy. Ma ona s² elementów macierzowych. Są to w ogólnym przypadku liczby zespolone, zatem mamy do czynienia z 2s² parametrami rzeczywistymi. Muszą one spełniać s warunków hermitowskości i warunek unormowania, a więc operator statystyczny zależy od (s-1) niezależnych parametrów [3].

Zbadamy własności macierzy gęstości światła w dwóch szczególnych przypadkach. Łatwo sprawdzić, że macierz gęstości światła całkowicie niespolaryzowanego ma postać

. (9.12a)

Bo prowadzi ona do wyrażenia (9.3b). Gdy mamy do czynienia z układem, którego bazy liczą s wektorów, macierz gęstości stanu całkowicie niespolaryzowanego ma postać

. (9.12.b)

Niech układ z prawdopodobieństwem
, znajduje się w stanie kwantowym
, a w pozostałych stanach ortogonalnych do
z może się znaleźć z prawdopodobieństwem
,
. W takiej sytuacji będziemy wtedy mówili o stanie czystym układu. Wtedy średnia wartość dowolnego operatora
związanego z jakąś własnością układu równa jest

. (9.13)

Od angielskiego słowa pure (czysty) operator statystyczny stanu czystego oznaczyliśmy przy pomocy dolnego wskaźnika p.

Ze wzoru porównania wzorów (9.4) i (9.13) widać, że macierz gęstości stanu czystego
ma postać operatora rzutowania

(9.14)

Ponieważ operator
jest idempotentny to układ kwantowy znajduje się w stanie czystym wtedy i tylko wtedy gdy

. (9.15a)

Zatem ślad operatora statystycznego stanu czystego spełnia warunek

. (9.15b)

Dla operatora statystycznego stanu czystego suma stojąca po lewej stronie nierówności (9.11b) osiąga największą wartość równą jedności. I odwrotnie - gdy ta suma osiąga wartość 1 to układ znajduje się w stanie czystym.

Literatura

[1] G. Baym, Lectures on Quantum Mechanics, Benjamin, Reading, Mass., 1974.

[2] R. Feynman, Mechanika statystyczna, Warszawa, PWN, 1974, § 1.

[3] P. Roman, Quantum Mechanics, an Advanced Course, Addison-Wesley, Reading, Mass.

§ 1.8.

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---