Zmiany Stanu skupienia wymagają dostarczenia energii mimo ze nie wzrasta temp Topnienie Q=qt*m Q- ciepło dostarczone qt ciepło topnienia Ciepło topnienia jest równe ilości energii potrzebnej do stopienia jednostki masy substancji bez zmiany temperatury
Parowanie Q=qp*m qp - ciepło parowania w określonej temperaturze Ciepło parowania jest równe ilości energii potrzebnej do wyparowania jednostki masy substancji bez zmiany temp Parowanie zależy tylko na powierzchni swobodnej cieczy.
Wrzenie szczególny przypadek parowania zachodzący w całej objętości cieczy Temp wrzenia zależy od panującej w niej ciśnieniu
Lorentza siła, siła działająca w polu elektromagnetycznym na poruszającą się cząstkę o ładunku e, z prędkością v, opisuje ją wzór: F=eE+(e/c)*(vxB), gdzie E - wektor natężenia pola elektrycznego, B - wektor indukcji pola magnetycznego (indukcja), c - prędkość światła, symbol "x" oznacza iloczyn wektorowy (wszystkie wielkości zmierzone w jednym układzie odniesienia). Pierwszy składnik wzoru przedstawia siłę działającą na cząstkę w polu magnetycznym Drugi siłę działającą w polu magnetycznym ( ta ostatnia powoduje zakrzywienie toru cząstki) Działanie siły Lorentza na elektrony w metalach i półprzewodnikach prowadzi do występowania zjawisk termomagnetycznych i Na wykorzystanie siły Lorentza oparte jest działanie akcelatorów soczewek magnetycznych
Półprzewodnik Opór właściwy półprzewodników zawarty jest między 100-1011Ωm Należy do nich pierwiastki german krzem oraz pewne związki metali np. tlenki miedziowy Cu2O, siarczek ołowiu PbS Zależność ich oporu od temp jest odwrotna niż metali Przy oziębieniu ich do temp zera absolutnego stają się izolatorami Opór ich szybko maleje przy podwyższaniu temp
Model pasmowy
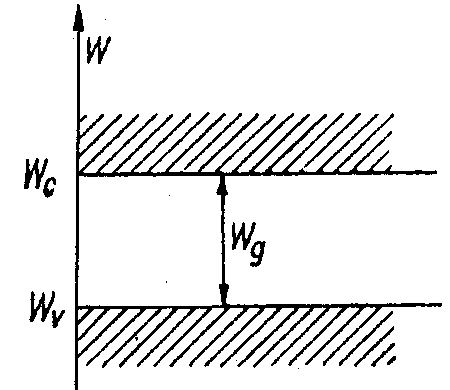
Wc - pasmo przewodni
Wr - pas podstawowe
Wg - pasm zabronione
Wg<2eV - półprzewod
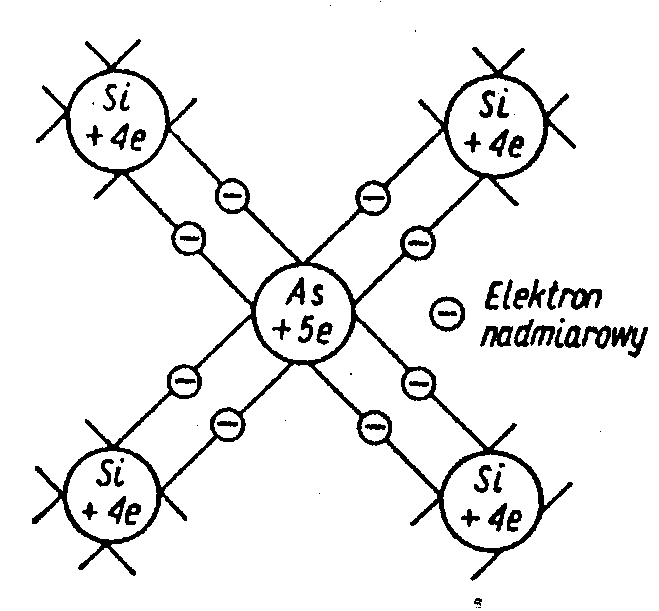
Półprzewodnik typu N Jeżeli w sieci krystalicznej Si wprowadzimy domieszkę pierwiastka pięciowartościowego np. arsen cztery elektrony domieszki wiążą się z elektronami sieci krystalicznej krzem natomiast jeden elektron domieszki jest słabo związany i może łatwo przejść do pasma przewodnictwa krzemu. Nośnik większościowy - elektrony Domieszkę tego typu naz donorową Nośnik mniejszościowy dziura

Przewodnik typ P Jeżeli w sieci krystalicznej Si wprowadzimy domieszkę pierwiastka z trzeciej grupy np. Al.+3to otrzymamy półprzewodnik typu p Trzy elektrony wiążą się z atomami krzemu jedno wiązanie jest niezupełne Wystarczy niewielka ilość energii aby elektron opuścił pasmo walencyjne pozostawiając swobodną dziurę która jest nośnikiem większościowym Domieszkę naz akceptorową
Prawo przesunięć promieniotwórczych Fajansa i Soddy'ego Rodziny promieniotwórcze
Jeżeli jądro pierwiastka promieniotwórczego wyrzuca cząstkę α o ładunku +2e i liczbie masowej 4 to atom tego pierwiastka zamienia się na atom pierwiastka o mniejszym o 2e ładunku jądra zatem pierwiastka xxxxxxxxxxxxczyli stojącej o dwa miejsca wcześniej w tablicy Mendelejewa. Oczywiście jego liczba masowa będzie o 4 jednostki mniejsza Jeżeli zaś atom wyrzuca cząstkę β jego jądro traci ładunek -e ładunek dodatni jądra powiększa się o +e w ten sposób powstaje jądro powstaje jądro pierwiastka stojącego o jedno miejsce dalej w tablicy Mendelejewa
Moment pędu , Kręt Wektor L prostopadły do płaszczyzny przechodzącej przez pkt nieruchomy O i wektor p Jego długość L=h*p=h*m*v gdzie h -ramie wektora p Łącząc dowolny pkt prostej na której leży wektor p z pkt O odcinkiem r o zwrocie od O do p możemy również zapisać L=rxp Moment pędu względem osi będzie moment rzutu wektora p na płaszczyznę z osią
Kręt ciała sztywnego
![]()
L=
Wszystkie cząstki ciała poruszają się z tą samą prędkościa kątową Vi=riω
L=∑miri2ω=Iω
![]()
Kręt ciała sztywnego równa się iloczynowi jego momentu bezwładności przez prędkość kątową Kręt elektronu
S=l/2
Równanie Schrodingera
Równanie ujmujące rzecz cząstki w polu potencjalnym
∂2Ψ/∂x2+∂2Ψ/∂y2+∂2Ψ/∂z2+8∏2m/h2(E-U)ψ=0 E-energia całkowita
U - energia potencjalna
Rozwiązanie równania Schrodingera daje w sposób naturalny i logiczny warunki kwantowe określające, że atom wodoru xxxxxx się znajdować tylko w pewnych oddzielnych określonych stanach energii
Dojście do równania Schrodingera
- równanie fali przestrzennej
∂2Ψ/∂x2+∂2Ψ/∂y2+∂2Ψ/∂z2=1/v2*∂2ψ/∂t2
zakładamy ze funkcja ψma kształt
ψ=ψ(x,y,z)sin2∏υt gdzie
amplituda drgań ψ jest funkcja tylko współrzędnych
∂2Ψ/∂x2=∂2Ψ/∂x2*sin2∏υt
∂2Ψ/∂y2=∂2Ψ/∂y2*sin2∏υt
∂2Ψ/∂z2=∂2Ψ/∂z2*sin2∏υt
∂2Ψ/∂t2=-4∏2υ2ψsin2∏υt
Podstawiając te wartość na drugie pochodne funkcji ψ do równania otrzymamy równanie
∂2Ψ/∂x2+∂2Ψ/∂y2+∂2Ψ/∂z2+4∏2υ2ϕ/V2=0
Założenie de Broglie'a
λ=h/mv
υ=v/λ=mv2/h
∂2Ψ/∂x2+∂2Ψ/∂y2+∂2Ψ/∂z2+4∏2m2v2ϕ/h2=0
E=U+mv2/2
ψ-Funkcja opisująca elektron w atomie lub cząsteczce
|ψ|2 - gęstość prawdopodobieństwa znalezienia elektronu w różnych xxxxxxxxx przestrzeni - rozkład gęstości elektronu
Teoria rozpadu atomowego -
dN=λNdt Jeżeli w pewnej chwili liczba atomów ciała promieniotwórczego jest N to liczba dN rozpadających się w czasie dt atomów jest proporcjonalna do N i do długości przedziału czasu dt
-dN jest ujemny przyrost czyli ubytkiem liczby atomów N
N=N0e-λt
N0 - liczba atomów danego ciała promieniotwórczego w chwili t=0
λ - stała rozpadu im λ większe tym pierwiastek szybciej się rozpada
T=ln2/λ czas połowicznego zaniku lub xxxxxx Po upływie czasu T połowa atomów danego pierwiastka zanika
Zjawisko Halla.
Polega na powstawaniu różnicy potencjału w przekroju poprzecznym przewodnika lub półprzewodnika w którym płynie prąd jeżeli przewodnik lub półprzewodnik znajduje się w polu magnetycznym.
UH=R (I B)/d I-natęż prądu, d-grub płytki.
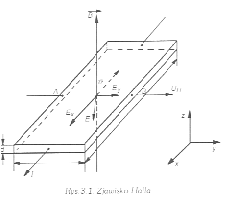
Pole magnetyczne działa na poruszające elektrony siłą Lorentza. F= -e(V x B) Siła ta powoduje zakrzywienie ruchu elektronu w kierunku jej działania wskutek czego powstaje nierównomierny rozkład gęstości elektronów.
Wytworzone pole elektryczne wywiera na elektronu siłę Fe=e EY która równoważy siłę F wstrzymując gromadzenie się elektronów. Jeżeli F=-Fe to powstaje różnica potencjałów zwana napięciem Halla.
Przemiany Gazu doskonałego Równanie stanu gazu doskonałego Równanie Clapeyrona
Przemiana izotermiczna T=const E izotermicznej przemianie stałej masy gazu ciśnienie jest odwrotnie proporcjonalne do objętości pV=const prawo Boyle'a Mariotte'a
pV=p1V1 p=p1*V1/V
Przemiana izobaryczna V=const W przemianie izobarycznej stałej masy gazu ciśnienie jest w prost proporcjonalna do temp w skali bezwzględnej prawo Charlesa p/T=const p/T=p1/T1 p=p1T/T1
Przemiana izobaryczna p=const Objętość określonej masy gazu pod stałym ciśnieniem jest wprost proporcjonalna do jego temperatury bezwzględnej Prawo Gay-Lussaca
V1=V2*T1/T2
Równanie stanu gazu doskonałego pV/T=const Dla określonej masy m gazu stosunek iloczynu jego objętości V i ciśnienia do temp bezwzględnej T stały i równy stosunkowi tych samych wielkości odniesienia do gazu w warunkach normalnych (V0 p0 T0) Wartość tego stosunku odniesienia do idealnego mola gazu jest dla wszystkich gazów jednakowa i nosi nazwę uniwersalnej stałej gazowej R V0*p0/T0=R stąd otrzymujemy pV=m/μ*RT m/μ dla N moli pV=RT równanie Clapa dla 1 mola
Porównanie przemiany izobarycznej i izochorycznej
-obie obie wymagają przepływu ciepła
- w obu następuje zmiana temperatury co pociąga za sobą zmianę energii wew
- w przemianie izochorycznej praca nie jest wykonywana
-w przemianie izobarycznej W=pΔV
- |Qr|<|Qp|
Qr=Cvm(T2-T1) Qp=Cpm(T2-T1)
Cv,Cp ciepło właściwe odpowiednie dla obu przemian
Ciepło właściwe i molowe ciał stałych i cieczy
Równowaga fazowa - tyle samo cząstek przewodzi z fazy ciekłej do stałej i odwrotnie np. woda z lodem ma równowagę fazową w temp 0C i ciśnienie 101325 Pa Temp równowagi fazowej nie jest stała dla danej substancji i zależy od ciśnienia
para nienasycona - w naczyniu występuje częściowe para wodna i woda która pasuje Zwiększa się masę pary oraz jej gęstość i ciśnienie Dopóki trwa ten proces mówimy o parze nienasyconej
para nasycona - gdy para osiągnęła największa gęstość
Diagram fazowy równowaga fazowa lodu wody pary
P pkt potrójny równowaga wszystkich 3 faz
p=611Pa T=273,15
C - woda przegrzana
K punkt krytyczny ciepło parowania =0
Sublinacja - zjawisko przemiany ciała stałego w parę z pominięciem fazy ciekłej
Resublinacja - odwrotnie niż sublinacja
Ciepło właściwe - ilość energii potrzebna do zwiększenia ΔU=cmΔt temperatury jednostki masy substancji (najczęściej 1 kg) o jeden stopień 1K
Ciepło molowe ilość energii potrzebna do zwiększenia temp o 1K jednego mola substancji C=Q/nΔT , n=m/μ → C=c*μ
Rozpad przez promieniowanie β
Przemiana β- emitowane są elektrony
Hipoteza Pauliego Podczas przemiany β- następuje w jądrze przemiana neutron w proton i elektron który wylatuje z jądra Ponadto w czasie tej przemiany pozostaje jeszcze w jądrze cząstka o masie spoczynkowej i ładunku równym zeru oraz xxxx równym 0,5h Cząstka ta zostaje nazwana neutrinem.
Widmo energii cząstki β-
Podział energii między elektron i neutron
energia elektron + energia neutrino = Emax
Przemiana β+ jądro emituje pozytony
powsta w wyniku przemiany proton w neutron
pozytoncząstka której masa jest równa masie elektronu a ładunek wynosi +e
Schemat przemiany β+ β--
A liczba Z liczba
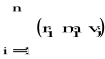
![]()
Wyszukiwarka
Podobne podstrony:
4054 a
4054
4054
4054
racjonalista 4054, Farmacja, Filozofia
4054
4054
4054
4054 4056
więcej podobnych podstron