POLITECHNIKA RZESZOWSKA

im. I. Łukasiewicza

Wydział Budowy Maszyn i Lotnictwa

Zakład Pojazdów Samochodowych

EKONOMIKA i ZARZĄDZANIE

w TRANSPORCIE SAMOCHODOWYM

PROJEKT NR 1.

Wykonał:

Arkadiusz Żywiec

V MDE

Konsultant:

dr inż. P. Pawlus

Opis projektu

Niech P₁, P₂, P₃ będą trzema producentami wyrobów tego samego rodzaju. Wielkość produkcji w ustalonym czasie niech wynoszą a₁, a₂, a₃ jednostek. Niech Q₁, Q₂, Q₃, Q₄ będą odbiorcami, którzy potrzebują określonej ilości tej produkcji. Wielkości zapotrzebowań tych odbiorców niech wyniosą b­₁, b₂, b₃, b₄ jednostek. Całkowita wielkość produkcji jest równa całkowitej wartości zapotrzebowania. Niech będą określone jednostkowe koszty transportu od każdego producenta do odbiorcy C_ij - jest to koszt transportu jednostki produkcji.

	O1	O2	O3	O4
P1	C11	C12	C13	C14	a1
P2	C21	C22	C23	C24	a2
P3	C31	C32	C33	C34	a3
	b1	b2	b3	b4

Dane:

Zagadnienie transportowe polega na tym, aby całkowity koszt transportu był minimalny.

Oznaczam ilość towarów, którą od producenta P_i należy dostarczyć do odbiorcy O_j przez X_ij.

	O1	O2	O3	O4
P1	X11	X12	X13	X14	a1
P2	X21	X22	X23	X24	a2
P3	X31	X32	X33	X34	a3
	b1	b2	b3	b4

Kompletny plan rozdziału transportu ( dopuszczalne rozwiązanie bazowe) określam za pomocą metody DANTZIGA (reguły kąta północno-zachodniego).

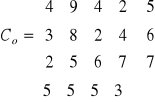
Jako pierwszą z macierzy wybieramy zmienną X₁₁. Jako wartość tej zmiennej przyjmujemy

. Ponieważ a₁ = b₁ odpowiednią daną kolumnę wykluczamy z planu transportu.

W każdym z przypadków a₁ zastępujemy przez
, zaś b₁ zastępujemy przez
.

Rozpoczynamy nowy tok obliczeń od zredukowania macierzy niewiadomych aż wszystkie zmienne zostaną określone jako bazowe.

Macierz X_o jest dopuszczalnym rozwiązaniem bazowym określonym za pomocą reguły kąta północno-zachodniego.

Funkcja celu FC wynosi:

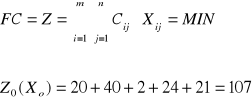
Minimalizacja kosztów transportu gdy znane jest dopuszczalne rozwiązanie bazowe, zostanie przeprowadzone drogą kolejnych iteracji.

Podstawiamy Θ_o za zmienną X_ij odpowiadającą najmniejszemu elementowi w macierzy C₁. Określamy jednoznacznie cykl wykreślając z macierzy X_o wszystkie kolumny zawierające tylko jeden element, a następnie z tak powstałej macierzy wykreślając wszystkie wiersze zawierające tylko jeden element.

Ponumerujemy elementy cyklu poczynając od Q_o jako pierwszego elementu. Macierz
otrzymamy, gdy od wszystkich parzystych elementów cyklu odejmiemy Q_o a do nieparzystych dodamy Q_o. Macierz X₁ powstanie gdy za Q_o podstawimy najmniejszy parzysty element cyklu.

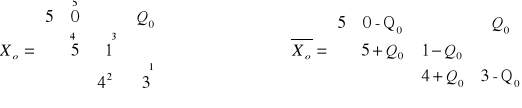
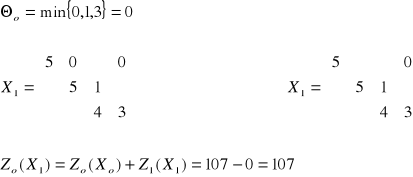
Rozważania prowadzimy tak długo, aż macierz kosztów C będzie zawierać tylko elementy nieujemne.

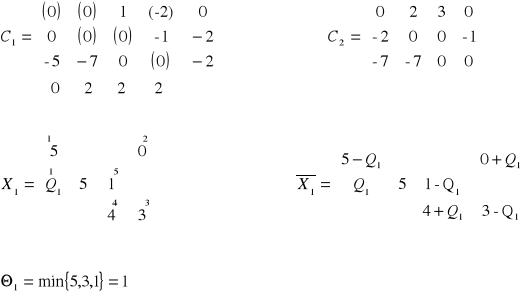
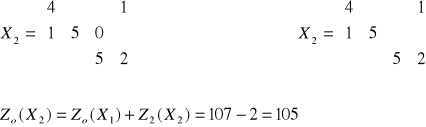
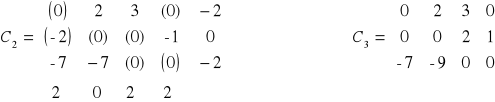
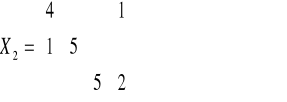
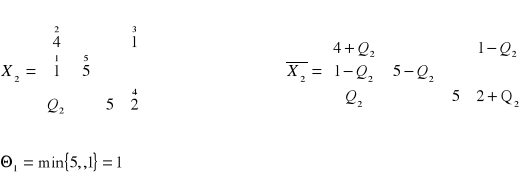
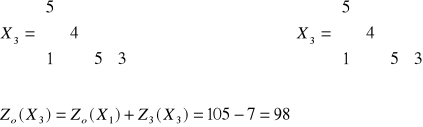
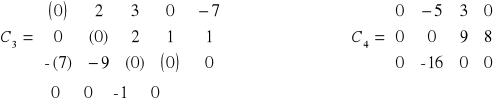
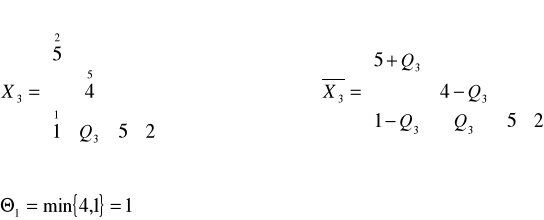
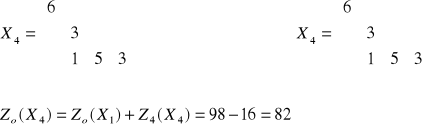
Macierz C₄ nie zawiera elementów ujemnych, więc X₂ jest rozwiązaniem optymalnym a minimalny koszt transportu wynosi 82.

3

5

początkowy koszt transportu

p_i^o

---