Wykład 1

• Protokół z Kyoto (1997): redukcja w latach 2008-2012

gazów ciepl. w tym CO2 o 5% w stosunku do roku 1990

• Prognoza rządowa URE (Polska) do roku 2020:

- nadal będą dominować elektrownie i elektroc. węglowe

- stabilizacja produkcji z elektrowni na węgiel brunatny

- do 2015 r. nie przewiduje się bud. elektrowni jądrowych

- udział energii ze źródeł odnawialnych do 2020r. - 12%

• Strategia energetyczna UE do roku 2020 (10.01.2007):

- redukcja gazów cieplarnianych o 20%

- w wytwarzanej energii 20% udział źródeł odnawialnych

- racjonalizacja zużycia energii o 20%

1. MASZYNY ELEKTRYCZNE I PALIWA W ENERGETYCE -
   WPROWADZENIE

1. Maszyny elektryczne w elektrowniach

Generatory synchroniczne jako źródła energii elektrycznej oraz silniki indukcyjne wspomagające pracę wielu układów potrzeb własnych bloków i potrzeb ogólnych elektrowni stanowią w schemacie technologicznym elektrowni podstawowe ogniwa.

Turbogenerator, jako maszyna współpracująca z turbiną parową, powinien pracować z możliwie dużą prędkością obrotową. Dla f = 50 Hz prędkość obrotowa turbogeneratora wynosi najczęściej n = 3000 obr/min, czemu odpowiada liczba par biegunów p = 1. Z kolei silniki indukcyjne stanowią podstawowy rodzaj napędu w układach potrzeb własnych elektrowni, takich jak: młyny węglowe, wentylatory powietrza i spalin, dmuchawy, sprężarki, pompy, mieszadła i przenośniki.

W energetyce polskiej moc elektrowni cieplnych stanowi około 97 %, a moc elektrowni wodnych zaledwie około 2,8 % ogólnej mocy elektrowni. Pozostałe 0,2 % to moc wytwarzana z tzw. odnawialnych źródeł energii, spośród których przyszłościowe znaczenie ma energia wiatrowa (por. rys. 1.1). Podane relacje wskazują zarazem na udział zainstalowanej mocy turbogeneratorów i hydrogeneratorów w systemie elektroenergetycznym.

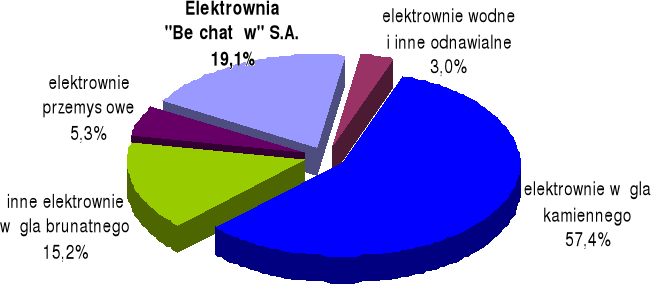
Rys.1.1.Udział poszczególnych elektrowni w produkcji energii elektrycznej w Polsce

Tablica 1.1. Moc zainstalowana w elektrowniach, [I1],[I2],[I3]

Nazwa elektrowni	Zainstalowana moc [MW]
Bełchatów	4320/4500*, (12x360MW)
Zespół PAK (Pątnów, Adamów, Konin)	2750, (Pątnów: 8x200MW, docel.4x225MW*)
Kozienice	2600/2820*, (8x200MW + 2x500MW)
Turów	2000, (4x500MW)
Zespół Dolna Odra	1900, (Dolna Odra:1600/1742*(8x200MW))
Połaniec	1800, (8x225MW)
Rybnik	1600, (8x200MW)
Zespół Jaworzno	1550, (Jaworzno III: 1350, (6x225MW))
Opole	1466, (1x376MW + 2x360MW +1x370MW)
Łaziska	1400
Łagisza	840
Siersza	740
Ostrołęka	693

*) moc zainstalowana po modernizacji

Prawidłowością jest wzrost granicznych mocy turbogeneratorów instalowanych w nowych elektrowniach. Są to moce największe jakie przy aktualnym stanie techniki można osiągnąć. Pozytywnym elementem jest wygoda gospodarowania dużymi jednostkami energetycznymi w eksploatacji oraz podczas realizacji nowych inwestycji. Jest oczywistym, że przy bardzo dużych obecnie mocach całego systemu energetycznego, zarządzanie wieloma jednostkami turbogeneratorów o mniejszych mocach utrudnia organizację procesu. Podobnie ma się rzecz z budową nowych elektrowni. Duży efektywny przyrost mocy instalowanej może być osiągnięty tylko w wyniku zastosowania jednostek o dużych mocach, bowiem koszty inwestycyjne budowy elektrowni oraz całkowita masa jednostkowa turbogeneratora wyrażona w [kg/kV·A], wykładniczo maleją wraz ze wzrostem mocy znamionowej instalowanej. Przykładem takiego podejścia może być projekt przedsięwzięcia inwestycyjnego o nazwie „Elektrownia Bełchatów II”, zakładającego budowę nowego bloku energetycznego z generatorem o mocy 833 MW. Obecnie 858 MW.

2. Wykorzystanie paliw w elektrowniach cieplnych

Odrębnym zagadnieniem jest udział poszczególnych nośników energii jako paliwa elektrowni cieplnych, których rola w krajowej energetyce jest dominująca. Dotychczas główną rolę w produkcji energii elektrycznej odgrywa węgiel kamienny. Jednak już od szeregu lat (lata dziewięćdziesiąte), jak też i obecnie, udział węgla brunatnego jako paliwa cieplnych elektrowni zawodowych utrzymuje się na poziomie (35÷40)%, co świadczy o jego strategicznej roli w gospodarce. Aktualnie zainstalowana moc w elektrowniach pracujących na węglu brunatnym (Bełchatów, zespół PAK, Turów) wynosi 9100 MW, co stanowi 31% mocy zawodowych elektrowni cieplnych. Przeprowadzone analizy wykazały, że istniejące w elektroenergetyce technologie węglowe będą, do końca 2005 roku, skutecznie konkurowały z technologiami wykorzystującymi inne nośniki energii, takie jak ropa naftowa i gaz ziemny. W związku z przystąpieniem Polski do Unii Europejskiej, wymagania dotyczące emisji zanieczyszczeń do środowiska (w szczególności przepisy dotyczące redukcji emisji dwutlenku węgla), spowodują po roku 2008 głęboką substytucję bazy paliwowej dla energetyki i ciepłownictwa. Dotychczasową procentową strukturę zużycia energii pochodzącej z nośników pierwotnych w Polsce, Niemczech oraz dla całej Unii Europejskiej w latach 1990 i 2000 charakteryzuje tab. 1.2.

Tablica 1.2 Struktura zużycia energii pierwotnej w Polsce, w Niemczech i w Unii Europejskiej, wg [A3]

Nośniki energii pierwotnej		Polska		Niemcy	Unia Europejska
				1990	2000	2000	2000
węgiel kamienny	%	61,6	50,0	13,4	12,1
węgiel brunatny	%	13,4	13,1	10,3	3,4
ropa i produkty naftowe	%	15,3	21,7	39,3	41,9
gaz ziemny	%	8,9	10,8	21,5	21,7
energia jądrowa	%	-	-	13,0	15,2
inne nośniki	%	0,8	4,4	2,4	5,7
ogółem	%	100,0	100,0	100,0	100,0

Wykład 2

2. Równania stanu generatora synchronicznego

1. Opis generatora w układzie osi naturalnych oraz rodzaje transformacji

Układ sześciu obwodów elektrycznych generatora synchronicznego: trzy symetryczne uzwojenia fazowe stojana (u, v, w) oraz trzy uzwojenia wirnika (uzwojenie wzbudzające f i dwa uzwojenia tłumiące D i Q działające w osi podłużnej i poprzecznej), można sprowadzić, wykorzystując teorię uogólnionej maszyny elektrycznej, do układu zastępczych uzwojeń stojana i wirnika, leżących w osiach wzajemnie prostopadłych i wirujących z określoną prędkością kątową ω_x [K10], [K18] - rys.2.30.

Rys. 2.1. Zastępcze obwody generatora synchronicznego;

1. układ osi magnetycznych uzwojeń fazowych u, v, w w powiązaniu z wirującym układem osi d, q (rzeczywisty układ uzwojeń)

2. zastępcze obwody generatora w osiach prostokątnych d, q

W układzie osi naturalnych u, v, w dla obciążenia symetrycznego ustalonego, zjawiska występujące w maszynie synchronicznej mogą być rozpatrywane tylko w czterech obwodach: u, v, w i f. W stanach nieustalonych, należy ponadto uwzględnić zwarte obwody zastępcze w wirniku, reprezentujące klatkę tłumiącą, kliny i inne masywne elementy wirnika maszyny, a w stanach niesymetrycznych dodatkowy obwód dla składowej zerowej prądu stojana. Zarówno w przypadku generatora z wirnikiem cylindrycznym, jak i z wydatnymi biegunami, większość zjawisk można zamodelować uwzględniając jedynie dwa zwarte obwody wirnika D i Q. W przypadku potrzeby dokładniejszej analizy, a zwłaszcza w celu dokładnego rozpatrywania zjawisk w masywnym wirniku, należy je rozważać wprowadzając większą liczbę obwodów tłumiących o różnych parametrach. Równania różniczkowe opisujące symetryczny stan elektromagnetyczny generatora w układzie współrzędnych naturalnych mają ogólną postać:

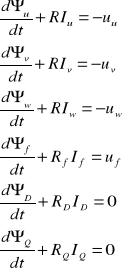
(2. 1)

We wzorach (2.1) rezystancję uzwojeń fazowych R_u = R_v = R_w oznaczono jako R oraz przyjęto, że u_k jest napięciem na zaciskach uzwojenia k o rezystancji R_k w którym płynie prąd i_k i z którym jest skojarzony strumień
. Występujące w równaniach (2.1) strumienie skojarzone wyrażają się wzorami ,[K10]:

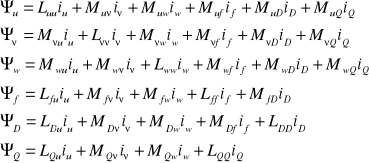
(2. 2)

gdzie:

L_uu, L_vv, L_ww i L_ff, L_DD, L_QQ - współczynniki indukcyjności własnej obwodów stojana i wirnika, natomiast:

M_uv = M_vu, M_uw = M_wu, M_vw = M_wv oraz

M_uf = M_fu , M_vf= M_fv , M_wf= M_fw , M_uD= M_Du ,M_vD= M_Dv , M_wD= M_Dw , M_uQ= M_Qu ,M_vQ= M_Qv
M_wQ= M_Qw - są współczynnikami indukcyjności wzajemnej obwodów fazowych stojana oraz stojana i wirnika.

Dla pełnego opisu nieustalonego stanu elektromechanicznego generatora, równania (2.1) należy uzupełnić równaniem równowagi momentów. Przy założeniu stałego momentu bezwładności zespołu wirującego oraz jednego tylko stopnia swobody ruchu obrotowego, równanie to ma postać:

- M_e (2.3)

gdzie:

J - moment bezwładności wirnika generatora i turbiny,

p - liczba par biegunów,

ω - elektryczna prędkość kątowa wirnika,

M_e - moment elektromagnetyczny generatora,

M_m - moment napędowy mechaniczny.

Współczynniki indukcyjności w maszynie z wydatnymi biegunami są w większości funkcjami okresowymi kąta γ określającego położenie wirnika, tzn. zmieniają się w czasie. Stąd też, wyznaczenie np. prądów zwarciowych w poszczególnych uzwojeniach maszyny w wyniku rozwiązania układu równań różniczkowych (2.2) i (2.3) jest dość uciążliwe.

W tym przypadku dąży się do przekształcenia tych równań w taki sposób, aby wyeliminować czasową zmienność współczynników indukcyjności własnej i wzajemnej. Spośród metod pozwalających na analizę nieustalonych stanów elektromechanicznych zachodzących w maszynie synchronicznej o m- fazowym zasilaniu (w szczególności trójfazowym), na uwagę zasługują metody wynikające z teorii transformacji elektromagnetycznych zmiennych stanu o współrzędnych fazowych, do innego układu współrzędnych prostokątnych wirujących (d, q) związanego z wirnikiem, lub układu nieruchomego (α, β) sztywno związanego z osiami uzwojeń stojana, [K19]. Transformowane zmienne stanu, to inaczej wektory przestrzenne takich wielkości układu m - fazowego, jak: prąd (I), napięcie (U) czy też strumień skojarzony (Ψ). Inne spotykane określenia wektora przestrzennego, to: uogólniony wektor, wektor zastępczy, czy też fazor przestrzenny.

Warto zaznaczyć, że prędkość wirowania ω_x układu osi prostokątnych może być dowolna, jednak najczęściej są stosowane następujące prędkości, determinujące zarazem rodzaj transformacji:

• ω_x = ω, dla układu d, q - transformacja na „płaszczyznę wirnika”, tzw. transformacja Parka - Goriewa,

• ω_x = 0, dla układu α, β - transformacja na „płaszczyznę stojana”, tzw. transformacja Edyty Clark i Stanley'a,

• ω_x = ω_s, dla układu współrzędnych x, y - transformacja na „płaszczyznę synchroniczną”, inaczej transformacja Krona.

Prędkość kątowa ω_s, oznacza synchroniczną elektryczną prędkość wirowania pola magnetycznego maszyny, wynikającą z m - fazowego symetrycznego i sinusoidalnego napięcia transformowanego uzwojenia.

Przykładowo przedstawiono przestrzenny wektor prądu stojana maszyny i jego transformację do układu współrzędnych d, q oraz α, β. Założono stan trójfazowego symetrycznego obciążenia bez składowej zerowej, określony prądami stojana

przy czym
,

(2.4)

Wówczas przestrzenny wektor prądu

I_s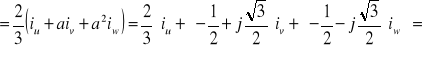
(2. 5)

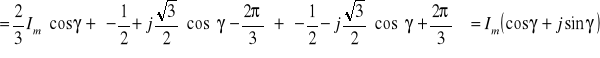
gdzie:

- operator obrotu o kąt
,

- operator obrotu o kąt
,

Przy transformacji tego wektora do układu d, q - Parka, na płaszczyźnie zespolonej wirnika wirującej z prędkością kątową ω, może on być przedstawiony w postaci

I_s
(2. 6)

Na podstawie zależności (2.5), uzyskuje się składowe wektora przestrzennego prądu

i_d = Re(I_s )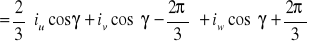
(2. 7)

oraz

i_q = Im(I_s )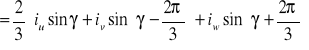
(2. 8)

Przy transformacji wektora przestrzennego I_s do układu α, β - E. Clark, otrzymuje się opis wektora na nieruchomej płaszczyźnie liczb zespolonych, o osi rzeczywistej skierowanej zgodnie z osią fazy u oraz o osi urojonej przesuniętej w kierunku wirowania o kąt
(rys. 2.2), w postaci

I_s =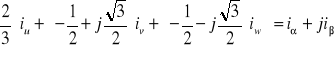
(2. 9)

przy czym: i_α = Re(I_s ) oraz i_β = Im(I_s ), a zatem

oraz
(2. 10)

W ogólnym przypadku, przy obciążeniu niesymetrycznym wyznacza się wektor przestrzenny dla prądów kolejności zgodnej i przeciwnej, a także kolejności zerowej (w układach trójfazowych z przewodem zerowym). Wówczas wypadkowy wektor przestrzenny wyraża się wzorem:

I_s = I_1s + I_2s + I₀ (2. 11)

Jednakofazowa składowa zerowa i₀ zawarta w prądach fazowych nie ma wpływu na wektory przestrzenne I_1s oraz I_2s i transformowana do układów zastępczych d, q oraz α, β, występuje w nich w odrębnym równaniu różniczkowym. Analogicznie, jak to podano dla prądu stojana, są tworzone wektory przestrzenne napięcia i strumienia skojarzonego oraz ich składowe w układach osi d, q i α, β.

Ogólnie można stwierdzić, że w analizie takich stanów generatora, w których stojan albo wirnik są niesymetryczne (mowa o symetrii w sensie magnetycznym i elektrycznym), jak to ma miejsce np. w przypadku zwarcia trójfazowego maszyny z wydatnymi biegunami, szczególnie przydatna jest metoda składowych d, q, gdyż eliminuje zmienność współczynników indukcyjności w czasie. Natomiast w przypadku, gdy niesymetryczne są zarówno stojan jak i wirnik, co występuje przy dwufazowym i jednofazowym zwarciu generatora z wydatnymi biegunami, w równaniach (2.1) przekształconych do układu osi d, q, czy α, β będą występowały zmieniające się okresowo współczynniki indukcyjności. Analiza tych zwarć w układzie składowych α, β okazuje się jednak prostsza.

1. Równania generatora w układzie współrzędnych d, q, 0

Transformacja Parka - Goriewa polega na zastąpieniu trzech uzwojeń fazowych stojana dwoma uzwojeniami umieszczonymi w osiach d, q wirnika, (rys. 2.1b). W ten sposób otrzymuje się w generatorze układ pięciu obwodów elektrycznych (d, q, f, D, Q) nieruchomych względem siebie, co eliminuje zmienne w czasie indukcyjności. Związki pomiędzy wielkościami elektrycznymi i magnetycznymi w obwodach zastępczych d, q oraz rzeczywistych u, v, w, wynikające z pojęcia przestrzennego wektora W dowolnej wielkości układu trójfazowego (prądu, strumienia czy napięcia), są następujące [K10]:

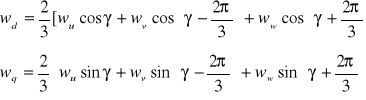
(2. 12)

Jeśli chcemy rozpatrywać w układzie składowych d, q dowolne przypadki asymetrii trójfazowych, należy do zależności (2.12) dopisać wyrażenie na składową zerową w₀

(2. 13)

gdzie:

w_u , w_v , w_w - wartości chwilowe wielkości w w uzwojeniach fazowych u, v, w.

Związki odwrotne

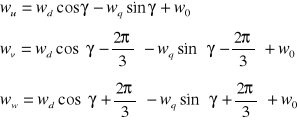
(2. 14)

Równania stanu generatora synchronicznego we współrzędnych d, q, 0 otrzymane z równań w układzie osi naturalnych (2.1) oraz równania momentów (2.3), po przekształceniach wynikających z przyjętej transformacji są następujące:

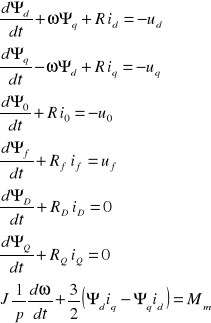
(2. 15)

gdzie:

,
- siły elektromotoryczne rotacji wynikające z zastąpienia nieruchomych uzwojeń u, v, w uzwojeniami d, q wirującymi z prędkością ω względem stojana,

- moment elektromagnetyczny

Strumienie skojarzone występujące w równaniach (2.15) są wielkościami niezależnymi od położenia wirnika i wyrażają się wzorami:

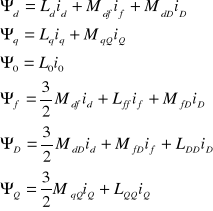
(2. 16)

Wynikiem transformacji Parka jest stosunkowo prosty układ równań różniczkowych liniowych. Występujące w tych równaniach skojarzenia magnetyczne są określone niezmiennymi w czasie współczynnikami indukcyjności, co stanowi największą zaletę opisanego przekształcenia.

2. Równania generatora w układzie współrzędnych α, β, 0

Jeżeli w maszynie trójfazowej zastąpić symetryczne uzwojenia u, v, w dwoma uzwojeniami α, β nieruchomymi względem stojana o wzajemnym układzie osi magnetycznych przedstawionym na rys. 2.2, to związki między wielkościami elektrycznymi lub magnetycznymi w tych uzwojeniach, wynikające z pojęcia wektora przestrzennego W oraz dla składowej zerowej są następujące [K10]:

Rys. 2.2.Wektor przestrzenny prądu stojana I_s w układzie osi prostokątnych nieruchomych α, β (założono i₀ = 0)

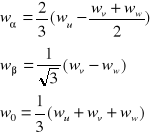
(2. 17)

Związki odwrotne

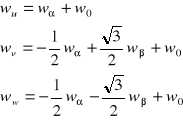
(2. 18)

Łatwo zauważyć, że równania stanu generatora wynikające z drugiego prawa Kirchhoffa dla zastępczych obwodów α, β będą analogiczne do równań (2.1) ponieważ wielkości fazowe u, v, w i wielkości α, β, jak to wynika ze wzorów (2.17) i (2.18), są związane między sobą zależnościami liniowymi i stałymi współczynnikami. Z fizycznego punktu widzenia można dodać, że w równaniach tych nie wystąpią siły elektromotoryczne rotacji, charakterystyczne dla układu d, q, gdyż uzwojenia α, β są nieruchome. Równania te uzupełnione równaniem równowagi momentów mają postać:

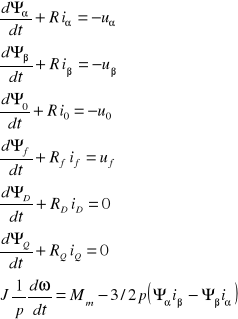
(2.19)

Wyrażenia określające strumienie skojarzone występujące w równaniach (2.19) są następujące:

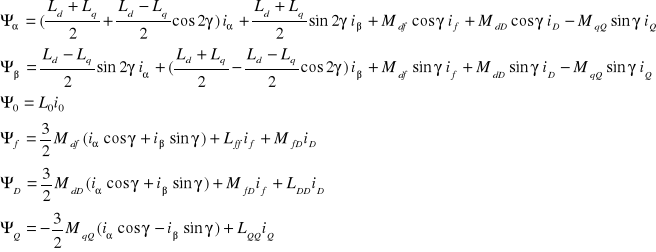
(2.20)

Rezultatem transformacji E. Clark wykorzystującej składowe α, β, 0 jest układ równań różniczkowych o zmiennych w czasie współczynnikach. Równania (2.19) opisują w sposób kompletny dynamiczne procesy elektromechaniczne występujące w generatorze synchronicznym i są szczególnie zalecane do analizy zwarć niesymetrycznych.

Transformacja Krona jest stosowana głównie w analizie stanów dynamicznych maszyn indukcyjnych i została szerzej omówiona w rozdziale 5 - „Silniki indukcyjne w układach potrzeb własnych elektrownii”.

---