Część pytań opracowałem sam na podstawie czarneckiego a cześć zerżnąłem z innych opracowań, który były zrobione również na podstawie czarneckiego. Mam dość! Wszystkiego!

Geodezja wyższa jest sztuką dla sztuki!!!! :-P

Objaśnij układ współrzędnych naturalnych; jak uzasadnisz przymiotnik „naturalnych”; jak można wyznaczyć położenie punktu w przestrzeni poprzez _P, _P, W_P.

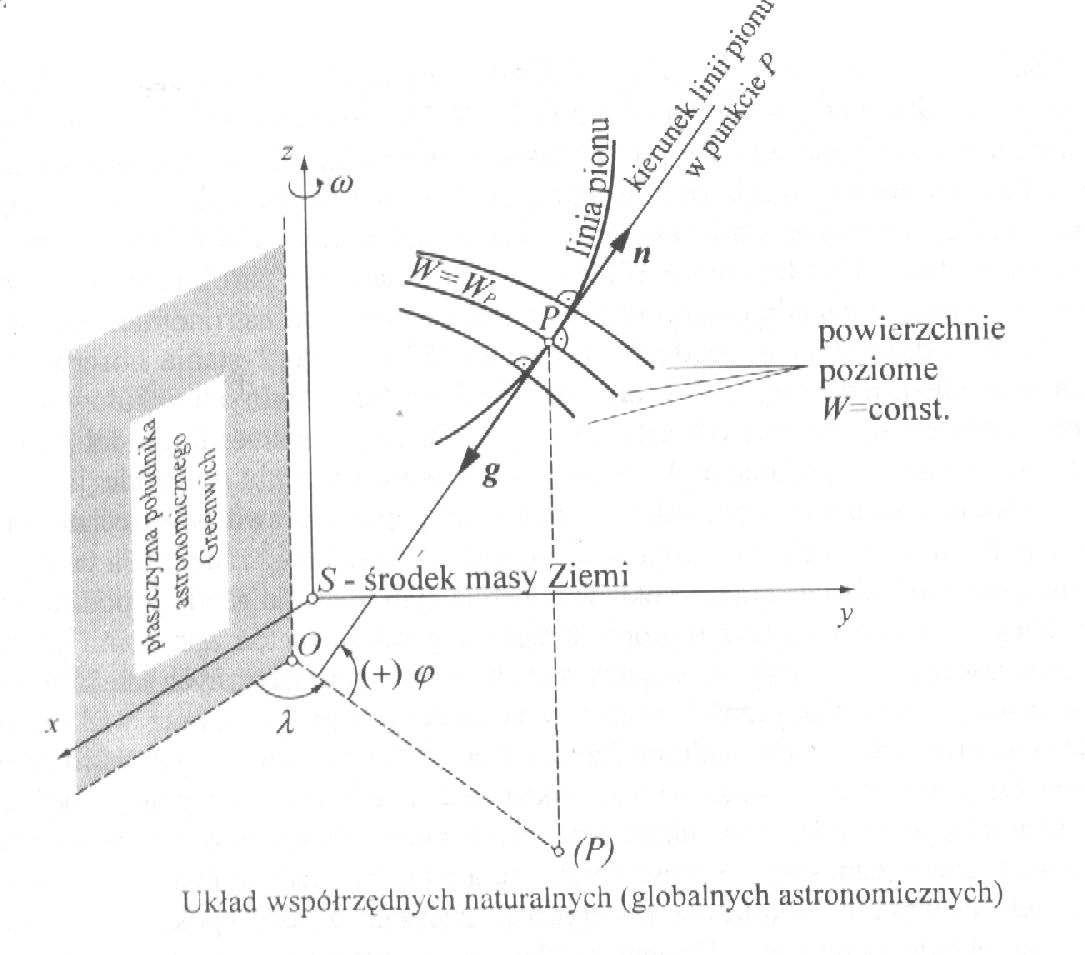
Kierunek linii pionu jest podstawą układu horyzontalnego, będącego z reguły lokalnym układem obserwacyjnym na pow. Z czyli układem który realizujemy za pomocą osi i płaszczyzn spoziomowanych instr obserwacyjnych. Związek tego układuz układem globalnym następuje poprzez tzw układ współrzędnych naturalnych. Osią układu jest chwilowa oś obrotu Z (
), przechodząca przez punkt S środka masy Z. Płaszczyzna przechodząca przez pkt S i prostopadła do osi obr nazywamy płaszczyzna równika astronomicznego. Przez kier linii pionu obserw. Greenwich prowadzimy pęk płaszczyzn wertykalnych i wybieramy tę która jest równoległa do (
) i nazywamy ją płaszczyzną południka astronomicznego Greenwich. Podobnie wyznacza się płaszczyznę południka w miejscu obserwacji w punkcie P.

Szerokość geograficzno - astronomiczna - kąt jaki tworzy kierunek linii pionu w pkcie P z płaszcz. równika ϕ (0^o - ±90^o)

Długość geograficzno - astronomiczna - kąt dwuścienny utworzony przez opisanie płaszczyzny południków astronomicznych (Greenwich i punktu P) λ(0^o - 360^oE lub 0^o - ±180^oE,W).

Kierunek linii pionu w pkcie P (g=gradW_p) można określić kątami ϕ i λ wyznaczanymi met. astr. Zdefiniowane kąty i wartość potencjału W tworzą trojkę wsp. naturalnych punktu P. W polu siły ciężkości możemy wyróżnić trzy powierzchnie ϕ=const λ=const W=const których przecięcie wyznacza punkt P.

Pokaż, że średni promień krzywizny elipsoidy obrotowej jest średnią geometryczną głównych promieni krzywizny.

Na podst. wzoru Eulera
możemy wyzn średni promień krzywizny jako granicy do której dąży średnia arytmetyczna krzywizn przekrojów normalnych w rozpatrywanym pkcie. Sumę nieskończenie wielu promieni krzywizn wyznaczamy z całki, której rozwiązaniem jest średni promień krzywizny

Przedstaw na rysunku szerokość geodezyjną i szerokość zredukowaną; wykaż, że maksymalna różnica szerokości geodezyjnej i szerokości zredukowanej osiąga wartość 5,8'.

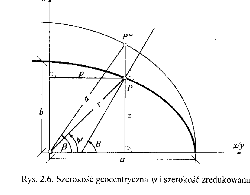
Szerokość zredukowaną otrzymujemy poprzez zrzutowanie punktu P na prostą równoległą do osi Oz z pow. elipsoidy na kulę o promieniu a. Promień wodzący rzutu pktu P tworzy z płaszcz. równika kąt β - szer. zredukowaną.

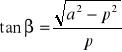
w przybliżeniu:
można więc oszacować

Podaj definicję oraz właściwości linii geodezyjnej na powierzchni elipsoidy obrotowej; omów właściwość linii geodezyjnej przedstawionej tzw. równaniem Clairauta; przedstaw przebieg linii geodezyjnej względem wzajemnych przekrojów normalnych.

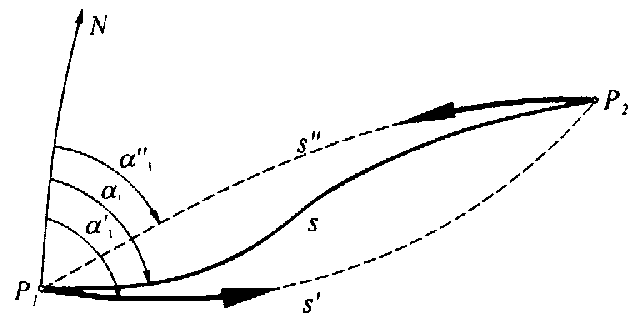
Normalne do powierzchni elipsoidy w P₁ i P₂ są wichrowate więc płaszczyzny przekrojów normalnych z P₁ do P₂ i z P₂ do P₁ nie pokrywają się. Rozbieżność przekrojów normalnych może dochodzić do 0,02” i trzeba ją uwzględniać przy obliczeniach. Linia geodezyjna na danej powierzchni to taka linia której normalna główna w każdym pkcie ma kierunek normalnej do powierzchni. Krzywizna geodezyjna

Równanie Clairauta: c = N cos B sin A = const Równanie to wyraża własność linii geodez. mówiącą o tym że iloczyn promienia równoleżnika( p=NcosB) i sinusa azmutu linii jest wielk. stałą.

Przedstaw istotę 2 znanych ci metod rozwiązywania trójkątów geodezyjnych

Trójkąt geod. - trójkąt na elipsoidzie obrotowej utworzony przez 3 łuki linii geodezyjnych. Małe trójkąty geod. o bokach < 90 km rozwiązujemy jako trójkąty o promieniu równym promieniowi krzywizny ze średniej szerokości wierzchołków.

Metoda additamentów (SOLDNERA )-polega na zamianie trójkąta sferycznego na płaski .Kąty pozostawiamy, mierzone boki pomniejszamy o tzw. additamenty ∂a,∂b,∂c

Wzorami trygonometrii płaskiej obliczamy boki b1,c1 i ich additamenty

Obliczamy boki trójkąta

sferycznego b= b1+∂b , c = c1+∂c

Dla trójkątów o bokach ≥ 200 km trzeba dokonać redukcji kątów ze wzorów Legendre'a

Metoda Legendra -mówi że mały trójkąt sferyczny możemy rozwiązać zamieniając go na płaski poprzez zmniejszenie

kątów o 1/3 nadmiaru sferycznego pozostawiając boki:

ε =( A+B+C ) - 180˚ 0 < ε < 2 π

A' = A - ε/3 itd.

Obliczamy boki b , c ze wzorów trygonometrii płaskiej otrzymując w rozwiązaniu boki trójkąta płaskiego równe bokom trójkąta sferycznego. Gdy boki trójkąta > 90 km posługujemy się rozszerzonym tw. Legendre'a.

Naszkicuj rysunki i objaśnij metodę Clarke'a rozwiązania `zadania wprost'

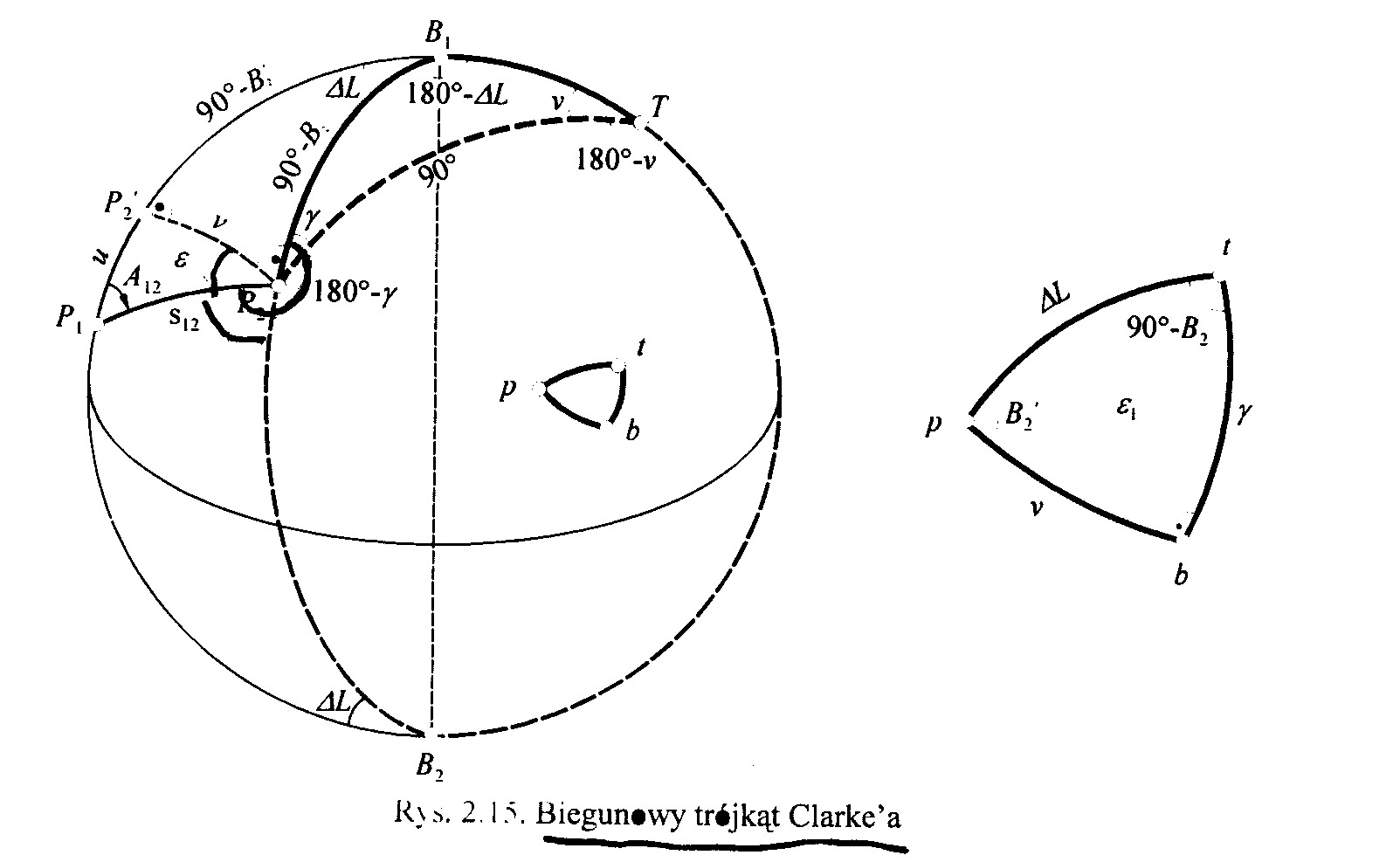
Mając dane wsp pktu P obliczamy średni promień krzywizny elipsoidy w tym punkcie R₁ Na kuli o takim promieniu rozwiazujemy mały prostokatny trojkat sferyczny P₁P'₂P₂ który powstał przez poprowadzenie przekroju normalnego w pkcie P₂ prostopadłego do południka punktu P₁.Rozwiązujemy trójkąt sferyczny P₁P'₂P₂ obliczając nadmiar sferyczny ε, przyprostokątne u, v i wyznaczamy szer. P'₂ sprowadzamy do kątowej wartości łuku na sferę o promieniu równym pr.krzywizny w P₂. Wyznaczamy długość L₂ za pomocą trójkąta pomocniczego p,t,b biegunowego względem trój. P₂ B₂ T. Rozwiązujemy trój. p t b twierdzeniem Legendre'a. Suma kątów w tym trój. daje nadmiar sfer. ε1.Poprawiamy każdy kąt w trójkącie o 1/3 ε i wyznaczamy azymut odwrotny A₂₁

1. obliczamy kąt zbieżności południk.

2. obliczamy β z trójkąta P P2′ P2

3. po zsumowaniu A2 = A2 ± 180° -γ -ε

Wskaż na powiązanie algorytmu całkowania numerycznego w obliczeniu współrzędnych (metody Kivioja) z twierdzeniem Clairaut'a dla linii geodezyjnej na powierzchni elipsoidy obrotowej.

Moim skromnym zdaniem powiązanie to polega głównie na tym, że dla każdego kolejnego elementu ds oblicza się (ze wzoru Clairaut'a) wartość azymutu w połowie tego elementu. Można przez to uzyskać lepsze przybliżenie przyrostu szerokości δB_i.

Przedstaw redukcje długości i redukcje kierunków w odwzorowaniu G-K.

Redukcja długości

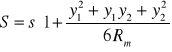
Długości S na płaszczyźnie są w odwzorowaniu G-K zawsze większe lub co najwyżej równe oryginalnym długościom na elipsoidzie S≥ s Na południku osiowym gdy y= 0, S= s

Redukcja kierunków

Wiernokątność odwzorowania odnosi się do kątów między liniami krzywymi. Kąty jakie tworzy cięciwa z łukiem krzywej boku trójkąta na płaszczyźnie oznaczone przez δ nazywamy redukcjami kierunków.

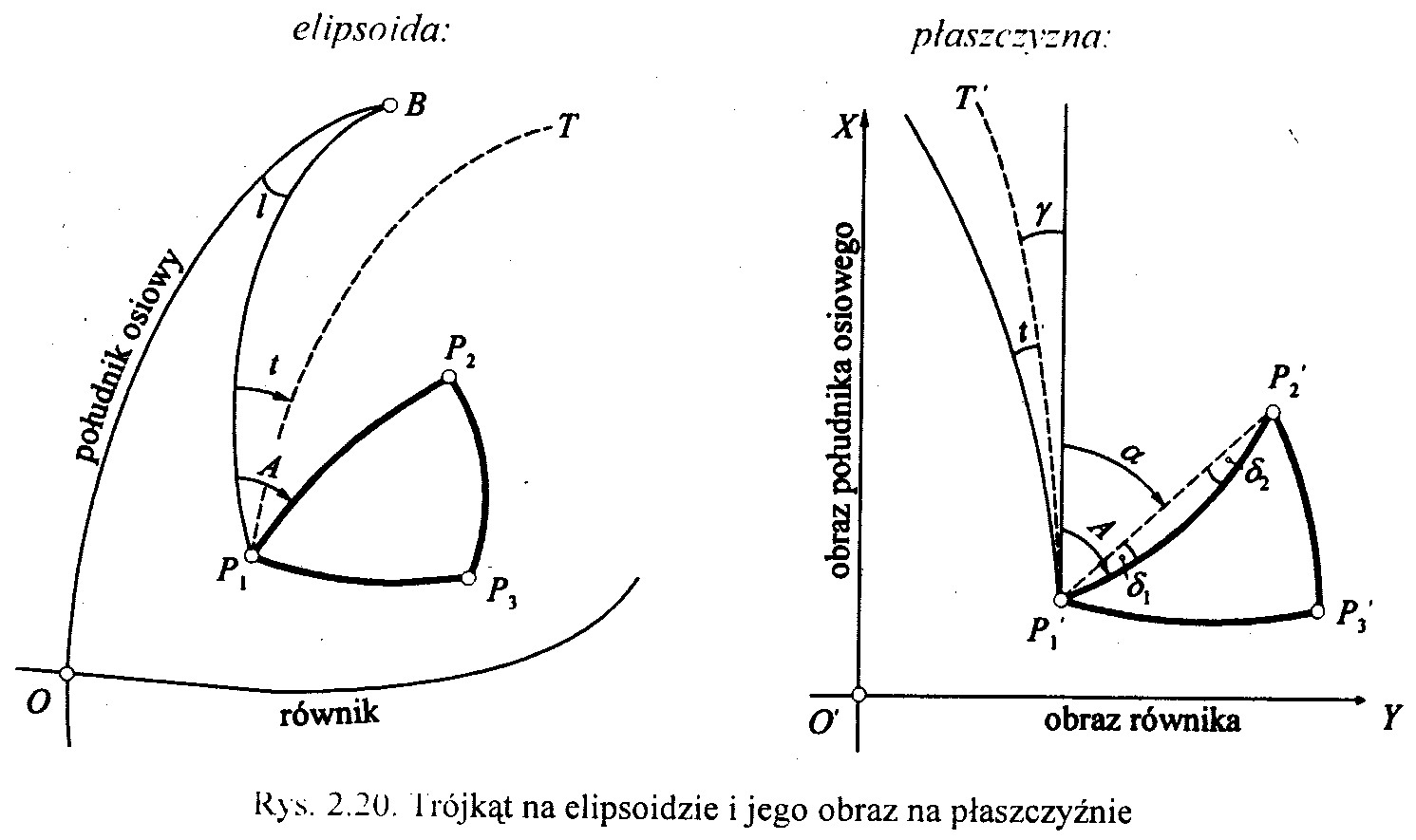
Wielkości α₁₂ w pkcie P₁' i α₂₁ w pkcie P₂' nazywa się kątami kierunkowymi. Suma kątów figury płaskiej wynosi: 360^o + δ₁₂ + δ₂₁ stąd ε = δ₁₂ + δ₂₁ Następnie robimy założenie że łuk krzywej P₁' P₂' jest łukiem kołowym tzn. δ₁₂ = δ₂₁

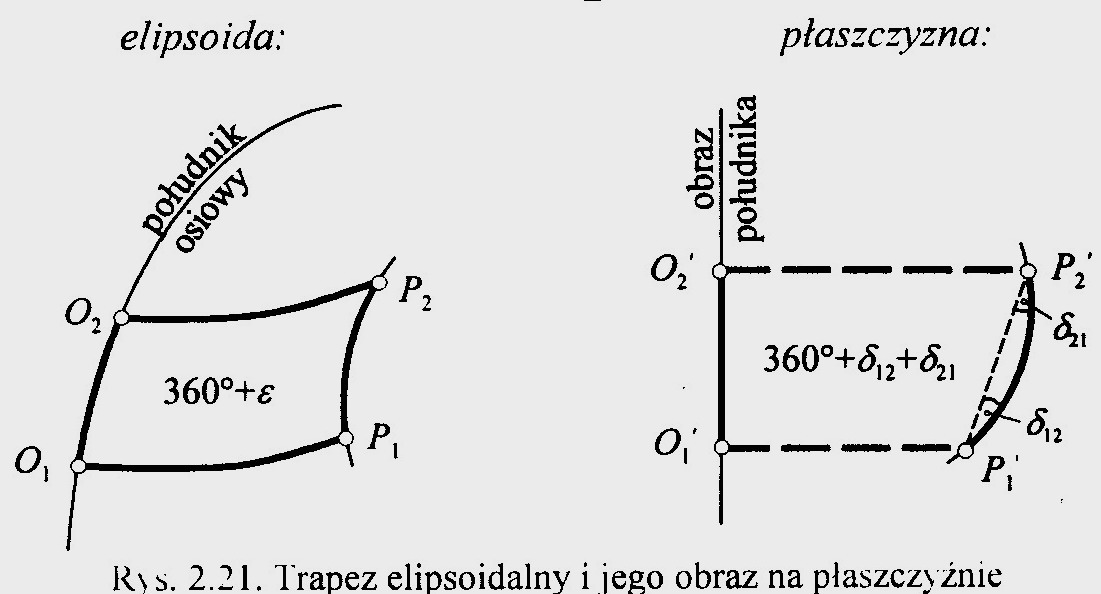
Przybliżony wzór przyjmie zatem postać:

Podaj definicję potencjalnego pola wektorowego oraz warunek potencjalności tego pola.

Pole wektorowe

Jeżeli każdemu punktowi pewnego obszaru (S)przyporządkowany jest jednoznacznie pewien wektor
w to ten obszar nazywamy polem wektorowym w

Potencjalne pole wektorowe

Jeżeli w obszarze (S) pole wektorowe w (P) jest gradientem pewnej funkcji skalarnej V(P) to nazywamy to pole potencjalnym polem wektorowym.

Warunek potencjalności

Operator Hamiltona ∇

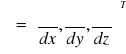
zwięźlej: gradV= ∇ * V

Rotacją albo wirowością pola wektorowego jest wektor rotw=∇×w

Dla potencjalnego pola wekt. ∇×w=∇×(∇V)=( ∇×∇)×V=0

Oznacza to, że pole jest bezwirowym, bezwirowość pola jest warunkiem potencjalności pola wektorowego. Inaczej: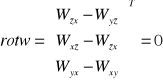
lub inaczej: W_zy=W_yz , W_xz=W_zx , W_yx=W_xy

Co rozumiesz pod pojęciem zagadnień brzegowych teorii potencjału? Objaśnij pierwsze, drugie i trzecie zagadnienie brzegowe.

Zagadnienie brzegowe to poszukiwanie wartości granicznych (brzegowych), które są potrzebne aby otrzymać rozwiązanie szczególne równań różniczkowych.

I zag. brzegowe - zagadn. Dirichleta - dotyczy problemu wyznaczania f. harmonicznych (potencjału) na zewnątrz pewnej powierzchni (S) na podstawie pewnych granicznych (brzegowych) wartości tych funkcji na pow. (S).

II zag. brzegowe - zagadn. Neumanna - wyznaczenie wartości potencjału w przestrzeni wewnętrznej lub zewnętrznej względem (S) dysponując pochodnymi normalnymi potencjału ∂V/∂n (względem zewnętrznej normalnej do (S).

III zag. brzegowe - zagadn. brzeg. geodezji fiz. - na powierzchni (S) znana jest kombinacja liniowa potencjału V i jego pochodnej w kierunku normalnej zewnętrznej do (S) w postaci: hV + k∂V/∂n h, k - stałe. Stanowi ono pewien model wyznaczania tzw. undulacji geoidy z anomalii grawimetrycznych.

Omów te własności wielomianów Legendre'a, które pozwalają na ich zastosowanie do rozwinięcia potencjału grawitacyjnego w szereg harmonicznych strefowych.

????????????????????????????????????????????????????????????????????????????????

Własnością tą jest ortogonalność. Warunki ortogonalności funkcji i wielomianów Legendre'a przedstawiają się następująco:

*całka iloczynu dwóch różnych funkcji lub wielomianów Legendre'a w granicach od -1 do 1 równa jest 0.

*całka iloczynu dwóch takich samych funkcji lub wielomianów Legendre'a wynosi: -1∫1[Pnm(x)] ↑2dx=2/(2n+1)*(n+m)!/(n-m)!

Warunki te rozwinięte na harmoniczne sferyczne prowadzą do wyznaczenia stałych współczynników c nm oraz s nm przy elementarnych harmonicznych sferycznych. Za pomocą tych ostatnich możemy przedstawić każdą funkcję harmoniczną np. potencjał grawitacyjny, który jest także funkcją harmoniczną.

???????????????????????????????????????????????????????????????????????????????????????

Pokaż na rysunku, a następnie objaśnij słowami użyteczność wielomianów P₂₀, P₃₀ do `modelowania' spłaszczenia Ziemi oraz niesymetrii rozkładu mas Ziemi względem płaszczyzny równika.

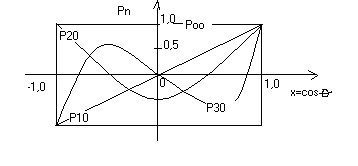
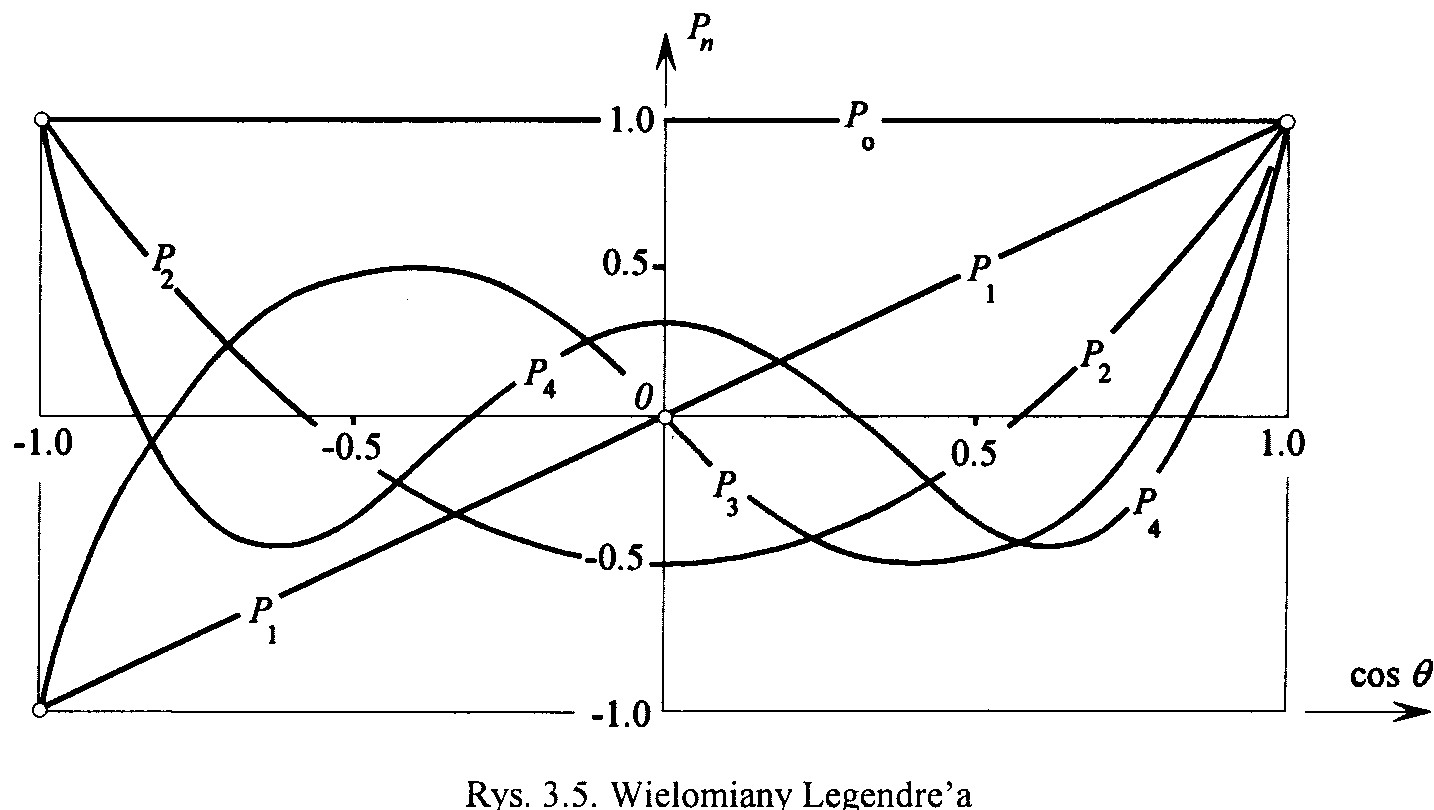
P₂₀=1/2*(3x²-1)

P₃₀= 1/2*(5x³-3x)

Współczynniki wielomianów (n+m) są pochodnymi wielomianu (x²-1)

P₂₀ służy do modelowania spłaszczenia Ziemi gdyż jest symetryczny względem równika (osi Pn). P₃₀ służy do modelowania rozkładu mas względem równika bo jest symetryczny względem osi ox (jest asymetryczny względem równika ) . Funkcje spełniające równania P₂ i P₃ są funkcjami sferycznymi strefowymi, zależą od ϕ i tworzą podział na (n+1) dla m=0 stref równoleżnikowych.

Przy jakich założeniach elipsoida ekwipotencjalna reprezentuje pole normalne siły ciężkości Ziemi?

• Rozmiar i kształt elipsoidy (a,f) są tak dobrane aby powierzchniabyła jak najlepszą aproksymacją geoidy

• masa elipsoidy jest równa masie Ziemi M

• prędkość kątowa wirowania elipsoidy wokół małej osi jest równa prędkości wirowania Ziemi ω

• powierzchnia przyjętej elipsoidy ma być z definicji powierzchnią ekwipotencjalną o potencjale U₀ równym rzeczywistemu potencjałowi siły ciężkości geoidy W₀

Podaj i omów przybliżony wzór na przyspieszenie normalne siły ciężkości.

γ = γ_a (1+f ^* sin²B - (1/4) f₄ sin²2B)

- spłaszczenie grawimetryczne

γ_a - przysp. na równiku f - spłaszczenie geometryczne

γ_b - przysp. na biegunie f₄ = f ( f^*+ (1/4) f )

Jak wyraża się przyspieszenie normalne ponad elipsoidę ekwipotencjalną.

Wyrażenie do wyznaczania wartości przyśpieszenia normalnego na wysokości h nad elipsoidą ekwipotencjalną:

Przy wyznaczaniu przyśpieszenia normalnego na niewielkiej wysokości h w przestrzeni zewn. elipsoidy ekwipotencjalnej używa się równania Brunsa odniesionego do przyśpieszenia normalnego γ.

Co to jest Geodezyjny System Odniesienia 1980? Uzasadnij, że 4 tzw. stałe standardowe stanowią kompletny zbiór danych do zdefiniowania pola normalnego siły ciężkości.

Geodetic Reference System 1980 - przyjęty XVII Zgromadzeniu Generalnym Międzynar. Unii Geodezji i Geofizyki w Canberze w grudniu 1979. System ten oparty jest na teorii geocentrycznej elipsoidy ekwipotencjalnej zdefiniowanej przez następujące stałe standardowe:

• równikowy promień Ziemi a=6378137m.

• geocentryczna stała grawitacyjna Ziemi(włączając atmosferę) GM=3986005*10⁸m³s^-2;

• kątowa prędkość Ziemi ω=7292115*10^-11rads-^1;

• dynamiczny współczynnik kształtu J₂=108263*10^-8;

Za pomocą 4 stałych standardowych można wyliczyć wszystkie wart. dynamiczne i geometryczne potrzebne do obliczeń związanych z elipsoidą odniesienia. Wg tw.

Stokesa rozmiar, kształt, masa i prędkość obr. definiują jednoznacznie funkcję wyrażającą potencjał normalny.

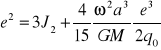
e² - wyznacza się iteracyjnie

Omów w zarysie geodezyjne efekty zjawisk pływowych.

Zjawiska pływowe są spowodowane przyciąganiem księżyca i słońca.

dla sztywnej Ziemi mamy trzy zasadnicze efekty zmian pływowych pola siły ciężkości:

• zmiana modułu wektora siły ciężkości,

• nachylenie powierzchni ekwipotencjalnej i jej przesunięcie.

• Inne efekty jak zmiana wysokości ponad geoidą czy elipsoidą, zmiany różnic wysokości, kątów, długości poziomych, czy zmiany odchyleń pionu można uważać za pochodne trzech zasadniczych. Odchylenie linii pionu określa stosunek składowej horyzontalnej do siły ciężkości.

dla elastycznej Ziemi

Siły pływowe powodują też deformację skorupy ziemskiej co powoduje zmianę kształtu Ziemi, a tym samym zmianę rozkładu mas. Zmiana rozkładu mas powoduje zmianę potencjału grawitacyjnego Ziemi.

Efekty zjawisk pływowych to zakłócenie wyników pomiarów: siły ciężkości, wysokości geoidy nad elipsoidą, wysokości elipsoidalnej, wysokości ortometrycznej oraz długości i kątów.

Objaśnij podstawowe równania geodezji fizycznej przedstawiając interpretację poszczególnych jego wyrazów. Jak rozumiesz `przybliżenie sferyczne' podstawowego równania.

Powierzchnie, do których odnoszą się obydwa składniki anomalii grawimetrycznej, to geoida i elipsoida ekwipotencjalna. Geoidę określa się, w zasadzie, tylko przez wyrażenie na potencjał W₀=const. W praktyce położenie geoidy względem punktów fizycznej pow. Ziemi wyznacz się przez długotrwałe obserwacje średniego poziomu mórz na stacjach mareograficznych, a następnie poprzez uśrednienie wyników tych obserwacji. Elipsoida ekwipotencjalna jest ściśle określona geometrycznie przez wymiar (a) i kształt (spłaszczenie f lub mimośród e), a ponadto jest powierzchnią ekwipotencjalną potencjału normalnego, którego wartość wynosi U₀=W₀. Trzeba zauważyć dodatkowo, że środek elipsoidy pokrywa się ze środkiem mas geoidy. Pokrywają się też obie osie maksymalnych momentów bezwładności obu brył. W celu rozwiązania podstawowego zadania geodezji - należy powiązać geometrycznie geoidę z elipsoidą poprzez wyznaczenie odległości obydwu pow. Taką odległość, liczoną od elipsoidy wzdłuż normalnej do tej pow., nazywamy wysokością albo odległością geoidy N.

Potencjał normalny U w punkcie P₀ na geoidzie można wyrazić poprzez potencjał na elipsoidzie U_e=U₀, gradient tego potencjału oraz odstęp N

Potencjał rzeczywisty W w tym samym punkcie P₀ przedstawiamy, jako sumę potencjału normalnego U i potencjału zakłócającego T:

W=U+T

W=U_e-γN+T

W związku z tym, że potencjały elipsoidy i geoidy są z założenia równe W=W₀=U_e, możemy podstawić W=U_e, a następnie napisać:

T=γN

Stąd zaś otrzymamy związek wielkości fizycznych - potencjałów geoidy i elipsoidy z wielkością geometryczną - wysokością geoidy względem elipsoidy w postaci wzoru Brunsa:

Zwróćmy uwagę, że wzór Brunsa jest zgodny z wzorami definiującymi wysokości, co widać gdy zapiszemy go w postaci:

Wyrażając potencjał zakłócający na fizycznej pow. Ziemi, w formie odnoszącej się do punktu P₀ położonego na geoidzie:

T=W₀-U

Zróżniczkujmy składniki tego wzoru względem normalnych n i n_e do powierzchni odpowiednio:W₀=const. i U=const. i niech to będą normalne zewnętrzne.

Bez istotnych konsekwencji można zaniedbać różnicę pomiędzy kierunkami n^→ i n^→_e , ponieważ kąt odchylenia pionu Θ jest mały i można uważać, że cosΘ=1, co oznaczałoby, że γ można wyrazić po prostu przez γ=∂U/∂n. Tworząc różnicę powyższych wyrażeń wynik różniczkowania można przedstawić:

Otrzymaliśmy wyrażenie pozornie podobne do anomalii grawimetrycznej. W anomalii grawimetrycznej przyśpieszenie normalne γ_e odnosi się do powierzchni elipsoidy ekwipotencjalnej; γ natomiast jest przyśpieszeniem normalnym na geoidzie. Różnicę γg przyśpieszeń rzeczywistego i normalnego, obu wziętych w tym samym punkcie, w szczególności na geoidzie, nazywamy zakłóceniem grawimetrycznym albo właściwą anomalią grawimetryczną. Zakłócenie grawimetryczne to po prostu pochodna potencjału zakłócającego w kierunku normalnej do pow. ekwipotencjalnej W=const. Przyśpieszenie normalne na geoidzie, można wyrazić poprzez przyśpieszenie normalne na elipsoidzie oraz gradient pionowy przyśpieszenia normalnego pomnożony przez wysokość geoidy względem elipsoidy:

Podstawiając za N wyrażenie z wzoru Brunsa:

Po podstawieniu ostatniego wzoru do:

oraz zaniedbaniu różnicy pomiędzy kierunkami n^→ i n^→_e , otrzymamy wyrażenie nazywane podstawowym równaniem geodezji fizycznej :

lub

Δg=δg+U_zzN

Równanie to wiąże anomalie grawimetryczne z zakłóceniami grawimetrycznymi oraz wysokościami geoidy względem elipsoidy. Drugi wyraz prawej strony równania bywa nazywany wyrazem Brunsa. Po zastąpieniu pow. elipsoidy ekwipotencjalnej pow. kuli o takiej samej objętości, otrzymamy:

Równanie to jest warunkiem brzegowym, mieszczącym się w tzw. trzecim zagadnieniu brzegowym teorii potencjału na pow. ekwipotencjalnej (geoidy), gdyż mamy w nim kombinację liniową potencjału zakłócającego i jego pochodnej w kierunku normalnej do pow. ekwipotencjalnej.

W jakim związku ze wzorami Stokesa pozostają wzory Vening-Meinesza? Przedstaw i omów te wzory.

W koncepcji Vening-Meinesz została wykorzystana zależność geometryczna pomiędzy wysokością geoidy ( wyrażona wzorem Stokesa ) a nachyleniem geoidy względem elipsoidy ekwipotencjalnej θ=dN-dN/ds., Rzutowanie kąta θ na południki na I wertykał daje składowe ξ i η . We wzorach na ξ i η mamy różniczki ∂N/∂ϕ i ∂N/∂λ które można wyznaczyć ze wzoru Stokesa.

Poprawka terenowa do pomierzonych wartości siły ciężkości.

Ma na celu obliczeniowe wyrównanie terenu wokół stanowiska aby wartość przyspieszenia odnosiła się do terenu płaskiego. Nadmiar masy po jednej stronie stanowiska i jej niedobór po drugiej powoduje zmniejszenie mierzonego przyspieszenia. Ponieważ nie jest możliwe opisanie terenu w sposób matematyczny poprawkę tą obliczamy dzieląc teren na koncentryczne walce, później na tak zwane segmenty wokół stanowiska. Poprawka stosowana jest do 30 km od stanowiska.

Przedstaw kolejne etapy redukcji grawimetrycznej Poincarego i Preya.

Jest to redukcja, która nie regularyzuje geoidy, ale też i nie zmienia jej masy. Redukcja ma na celu wyznaczenie - na podstawie pomierzonego na fizycznej pow. Ziemi przyśpieszenia g - wartości przyśpieszenia na geoidzie g_P-P, wartości takiej, jaka jest rzeczywiście na pow. geoidy, gdy rozkład przestrzenny mas ponad geoidą pozostaje niezmieniony. Efektem redukcji ma być przyśpieszenie siły ciężkości, jakie pomierzylibyśmy `zanurzywszy' przyrząd pomiarowy w masach skorupy ziemskiej na głębokość równą wysokości nad poziomem morza. Oczywiście, że redukcję można odnosić do dowolnego punktu położonego na linii pionu stacji pomiarowej, na której wyznaczono przyśpieszenie g, zaś nieskończenie do geoidy; może to być na przykład pkt. znajdujący się w połowie wysokości. Bardzo często przyśpieszenie siły ciężkości w takim właśnie punkcie będziemy uznawać jako przybliżenie przeciętnej wartości przyśpieszenia wzdłuż wysokości. Poprawki topograficzne do redukcji Poincarego-Preya oraz wykorzystanie jej do wyznaczania wysokości ortometrycznych wprowadził T. Niethammer.

Niech H oznacz wysokości stacji pom. o znanym przyśpieszeniu g ponad pow., na którą przyśpieszenie to chcemy zredukować w taki sposób, jakby to było przyśpieszenie na tej pow. pomierzone (może to być pow. geoidy). Etapy redukcji:

a)Wprowadzamy poprawkę terenową względem pow. ekwipotencjalnej punktu P, znajdującej się na wys. H. Poprawkę tę oznaczamy przez δg_t (+) oraz zauważymy, że jest ona dodatnia. W wyniku zostanie uformowana płyta Bouguera o wysokości H.

b)Usuwa się płytę Bouguera przez wprowadzenie redukcji Bouguera. Mamy więc następny składnik redukcji δg_B=-0,0419σH (-), który jest ujemny.

c)Wprowadza się redukcję wolnopowietrzną, aby przyśpieszenie odnieść do pkt. P₀ położonego na geoidzie. Redukcja δg_F=0,3086H (+) będzie dodatnia.

d)Przywraca się przyciąganie płyty Bouguera. Jest to przyciąganie oddziaływujące na punkt umieszczony pod płytą. Składnik redukcji δg_B= -0,0419σH (-), który ma wartość ujemną, bowiem zmniejsza przyśpieszenie w punkcie P₀.

e)Ostatni etap redukcji stanowi `przywrócenie' ukształtowania topograficznego (pow. Ziemi) poprzez poprawkę topograficzną, lecz tym razem w odniesieniu do punktu P₀. Oznaczamy tę poprawkę przez δg_t'. Ta poprawka może czsem być ujemna.

Różnicę poprawek topograficznych δgt i δg_t' oznaczamy δg_t

W terenie płaskim lub o nieznacznych deniwelacjach każda z tych poprawek jest niewielka, a zatem ich różnica zazwyczaj jeszcze mniejsza i w wielu przypadkach można te wpływy pominąć. Sumując wszystkie składniki redukcji Poincarego i Preya otrzymamy wzór:

δg_P-P=δg_F-2δg_B+δg_T

Przedstaw wysokości ortometryczne Nithammera i Helmerta.

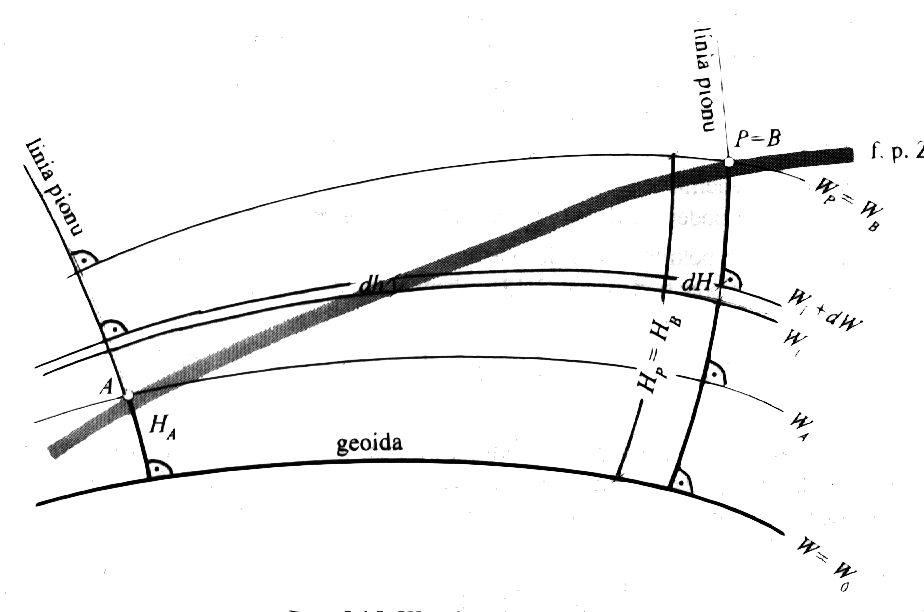
Wysokości te oznaczają odległości punktów fizycznej powierzchni Ziemi od geoidy mierzone wzdłuż linii pionu.

Ortometryczną różnicę wysokości między punktami A,B możemy wyrazić wzorem:

Natomiast poprawka ortometryczna (Niethammera) wyrazi się wzorem:
w którym:

,

zaś κ_A i κ_B są wyrażone w funkcji przeciętnych gęstości mas σ_A i σ_B na odcinkach linii pionu pomiędzy geoidą i punktami A i B oraz średniej gęstości skorupy ziemskiej σ_m.=5.52 gcm^-3. Poprawki i wysokości wyznaczone za pomocą powyższych wzorów nazywa się prawdziwymi poprawkami ortometrycznymi i prawdziwymi wysokościami ortometrycznymi. Poprawka ortometryczna Niethammera najbardziej szczegółowo obejmuje uwzględnienie rzeczywistych gęstości skorupy ziemskiej i ukształtowania powierzchni terenu. Praktyczne wyznaczenie poprawek ortometrycznych Niethamera jest bardzo uciążliwe. Trzeba dysponować wartościami gęstości skorupy ziemskiej w wielu punktach.

Uproszczenie we wzorze Niethamera poczynił Helmert. Zrezygnował z poprawek terenowych
i
w punktach A i B, które będą niewielkie, a w terenach płaskich i nieznacznie pofałdowanych wręcz znikome.

Wysokości ortometryczne uzyskane prze zastosowanie takiego wzoru noszą nazwę przybliżonych wysokości ortometrycznych. Na niewielkich obszarach objętych niwelacją można założyć jedną gęstość dla całego obszaru κ_A=κ_B=κ , otrzymamy wzór na poprawkę ortometryczną:
.

Jakie parametry pola siły ciężkości umożliwiają wyznaczenie krzywizny linii pionu?

Wektor krzywizny linii pionu leży w płaszczyźnie zawierającej wektor gradientu horyzontalnego przyspieszenia ∂g/∂s tzn. w płaszczyźnie ściśle stycznej do linii pionu. Wyznaczenie krzywizny linii pionu jest możliwe poprzez uzyskanie przyspieszenia w rejonie punktu danego i gradientu horyzontalnego przyspieszenia lub przyspieszenia w rejonie punktu danego i potencjałów Wxz i Wyz.

Co to jest względne odchylenie pionu? Jak można wyznaczyć wartości względnych odchyleń pionu w punktach nie będących stacjami astronomicznymi?

Odchyleniem pionu nazywamy kąt θ jaki tworzą kierunki wektorów g₀ (wektor przyśpieszenia rzeczywistego na geoidzie ) i γ₀ (wektor przyśpieszenia na elipsoidzie)

ξ,η - składowe odchylenia pionu ξ=ϕ - B η = (λ - L)cosϕ dla

ϕ,λ - zredukowanych na geoidę

ξ - rzut kąta θ na południk η - rzut kąta θ na pierwszy wertykał

Względne odchylenia pionu zależne są od parametrów elipsoidy (gdy te ulegną zmianie zmieni się normalna do elipsoidy a tym samym odchylenie pionu).

Względne odchylenia pionu możemy obliczać astronomicznie jak i grawimetryczne (wzory Vening - Meinesza ), odchylenia te różnią się.

W punktach stacji astrononicznych mamy wyznaczone względne odchylenia pionu obliczone astronomicznie jak i grawimetryczne możemy więc utworzyć ich różnicę.
,

Jeżeli przyjmiemy, że różnice te pomiędzy sąsiednimi stacjami zmieniają się quasi - liniowo. Można by więc przeprowadzić liniową interpolację różnic Δξ i Δη pomiędzy stacjami astronomicznymi. Trzeba mieć co najmniej 3 stacje astronomiczne, aby na podstawie różnic Δξ i Δη wyznaczyć 6 współczynników interpolacyjnych x₀ ,y₀ ,x₁ ,y₁ ,x₂ ,y₂

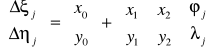
Wziąwszy odpowiednie dla każdego punktu ϕ_j i λ_j , oblicza się względne odchylenia pionu , dodając wyinterpolowane różnice do odchyleń grawimetrycznych : .
,

W praktyce okazało się, że złożenie o liniowych zmianach różnic Δξ_j i Δη_j nie bywa spełnione z dostatecznym przybliżeniem. Sprawiało to, że odległość pomiędzy stacjami astronomicznymi musiała być skracana nawet aż do około 70 km.

Niwelacja astronomiczno - grawimetryczna

Takim terminem określa się procedurę wyznaczania różnic wysokości geoidy względem elipsoidy odniesienia w punktach sieci astronomiczno - geodezyjnej na podstawie odchyleń pionu.

,
gdzie:

α-azymut zrzutowanego odchylenia pionu na płaszczyznę przekroju normalnego.

Wyznaczenie różnic wysokości geoidy za pomocą odchyleń pionu, które wyznaczono za pośrednictwem metody grawimetrycznej, nazwano niwelacją astronomiczno-grawimetryczną.

Objaśnij redukcję szerokości i długości astronomicznej na geoidę w rzeczywistym polu siły ciężkości. Wskaż te elementy redukcji, które dotyczą pola normalnego siły ciężkości.

Głównymi składnikami redukcji są szerokość ϕ' i długość λ' zaobserwowane na fizycznej powierzchni Ziemi. Szerokość geodezyjna B i długość geodezyjna L jest przedstawiona wzorami:

B=ϕ'+δϕ+δB ; L=λ'+δλ+δL,

przy czym δB=-ξ^ag; δL=-ηsecϕ wyrażają odchylenia pionu astronom-geod wyzn ze wsp. astro i geod,

δϕ i δλ (szukane elementy) oznaczają zmianę kierunku pionu wynikającą z krzywizny linii pionu.

δϕ≈ [(-Hf*/M)sin2ϕ]-[(H/γ)(∂Δg/∂x)]

δλ≈ -(H/λ)(∂Δg/∂y)secϕ

[(-Hf*/M)sin2ϕ]- dotyczy redukcji w polu normalnym. δϕ i δλ obliczamy za pomocą średniego promienia równika, przeciętnej wartości przyspieszenia normalnego, promienia krzywizny południka i spłaszczenia grawimetr.

Przedstaw definicję wysokości normalnych Mołodeńskiego. Na czym polega różnica pomiędzy ścisłym i przybliżonym podejściem do wyznaczenia wartości wysokości normalnych?

Wysokością normalną nazywamy iloraz H=c/γ, gdzie c- liczba geopotencjalna (różnica potencjału geoidy i potencjału powierzchni przechodzącej przez punkt), γ- przeciętna wartość przyspieszenia normalnego siły ciężkości między elipsoidą ekwipotencjalną a telluroidą. Ścisłe wyznaczenie wysokości normalnych możemy otrzymać poprzez całkowanie wzoru na przyspieszenie normalne dla wysokości h ponad elipsoidą. Dzięki procesowi iteracyjnemu możemy dokładnie wyznaczyć wysokość normalną. Przybliżoną wysokość normalną otrzymujemy z różnicy wysokości normalnych. Różnica ta jest sumą poprawki normalnej (wyznaczanej z przeciętnej przyspieszenia normalnego na elipsoidzie dla średniej szerokości i średniej wysokości) i sumy pomierzonych różnic wysokości.

Grawimetry statyczne: omów jeden ze znanych ci modeli grawimetru statycznego.

Grawimetry statyczne służą do pomiaru względnego przyspieszenia siły ciężkości. Grawimetrem statycznym jest pionowa sprężyna obciążona stałą masą. Ze zmiany przyspieszenia siły ciężkości wynika zmiana długości sprężyny. Przyspieszenie siły ciężkości jest zrównoważone siłą sprężyny: mg=k(l-lo), gdzie k- stała danej sprężyny, l- długość sprężyny obciążonej, lo- długość sprężyny nie obciążonej. Zmianę przyspieszenia siły ciężkości Δg możemy obliczyć różniczkując powyższy wzór.

Opisz znane ci poprawki pomiarów grawimetrami.

Poprawki eliminujące wpływ warunków zewnętrznych:

- temperatura- grawimetr powinien być kalibrowany w różnych temperaturach, do obliczeń należy przyjmować współczynnik temperat., do systemu mierzącego stosuje się kompensację i izolację termiczną

- ciśnienie atmosferyczne- zmiana powoduje zmienne przyciąganie mas atmosfery i deformacje skorupy ziemskiej pod wpływem mas atmosfery. Badamy zależność zmian grawitacji od ciśnienia metodą teoretyczną i eksperymentalną

- popr. pływowa-deformacje spowodowane oddziaływ. księżyca i słońca powodują na skorupie ziemskiej rozbieżności 40-60 cm na lądach i 10 cm na oceanach. Aby obliczyć poprawkę wprowadzamy współczynnik grawimetru, przyspieszenie ziemskie, paralaksę równikową i odległości zenitalne księżyca i słońca

Poprawki instrumentalne:

- nieliniowość skali licznika grawimetru- wyznaczana podczas kalibracji i dodawana do odczytu grawimetru

- poprawka chodowa- dryft polega na zmianie miejsca zera grawimetru i dlatego wprowadzamy czas pomiaru. W celu ustalenia poprawek obserwacje na tych samych pkt. powtarzamy w określonych odstępach czasu

Omów ogólne zasady transformacji współrzędnych geodezyjnych.

Zadanie transformacji między dwoma układami geodezyjnymi polega na obliczeniu współrzędnych w układzie wtórnym dla punktów, których współrzędne znane są w układzie pierwotnym na podstawie współrzędnych pewnych punktów „łącznych” znanych w obu układach. Punkty łączne służą do określenia modelu transformacji, gdy jednak model jest znany w postaci ogólnych związków matematycznych pomiędzy współrzędnymi w obu układach punkty łączne stanowią podstawę do wyznaczenia parametrów transformacji.

Przypadki transformacji:

- klasyczny gdy punkty łączne pokrywają tylko nieznaczny obszar wspólny obydwu układów

- metody pomiarów satelitarnych gdzie punkty objęte obydwoma układami przenikają się całkowicie

- punkty należące do układu satelitarnego wiążą ze sobą obydwa układy.

Omów transformację afiniczną współrzędnych x, y, z; przedstaw zawężenie modelu transformacji do jednego współczynnika skali (transformacja 7-parametrowa).

Jest przejściem z jednego układu do drugiego za pomocą param transformacji.

Nachylenie dwóch prostokątnych układów wsp. określa się za pomocą kątów obrotów α,β,γ, zniekształcenia w poszczególnych kierunkach osi układu oraz wektora przesunięcia początku układu.

Transformacja 7-mio parametrowa (Bursy- Wolfa) układa się trzy macierze obrotów elementarnych i składa w macierz obrotu. Kwadrat wiersza lub kolumny macierzy obrotu ma spełniać warunek ortogonalności to znaczy równać się 1 a iloczyn 2 wierszy lub kolumn 0. Macierz ta zapewnia 1 cm. dokładność obliczeń.

r_i″=(1+κ)R(α,β,γ)r_i'+r₀ ;

Podaj definicje niwelacji satelitarnej; omów zasadnicze podejście do niwelacji satelitarnej w skali globalnej i regionalnej.

(skala globalna i regionalna)

Nazywamy czynności których rezultatem jest wyznaczenie wysokości ortometrycznych na podstawie wys. geometr. wyznaczanych techniką satelitarną GPS oraz informacji o ziemskim polu siły ciężkości które pozwalają wyznaczyć odstęp geoidy od elipsoidy N. Do regionalnych wyznaczeń model potencjału grawitacyjnego wprowadzamy regionalne i lokalne anomalie grawim. a w podejściu lokalnym numeryczne modele terenu. Są trzy sposoby wyznaczenia geoidy w skali globalnej:

- całkowanie anomalii grawimetrycznych za pomocą wzoru Stokesa

- kolokacja metodą najmniejszych kwadratów (możemy włączyć różne dane np: astronomiczne odchylenia pionu, wys. ort. znane z niwelacji)

- szybka transformacja Fouriera (obliczamy N na płaszczyźnie lub w nowszych rozwiązaniach sferze) jest to metoda do obliczenia całki Stokesa.

---