 | Pobierz cały dokument wyzsza.gik.semestr.4.wyzsza.gw.doc Rozmiar 928 KB |
Część pytań opracowałem sam na podstawie czarneckiego a cześć zerżnąłem z innych opracowań, który były zrobione również na podstawie czarneckiego. Mam dość! Wszystkiego!
Geodezja wyższa jest sztuką dla sztuki!!!! :-P
Objaśnij układ współrzędnych naturalnych; jak uzasadnisz przymiotnik „naturalnych”; jak można wyznaczyć położenie punktu w przestrzeni poprzez P, P, WP.
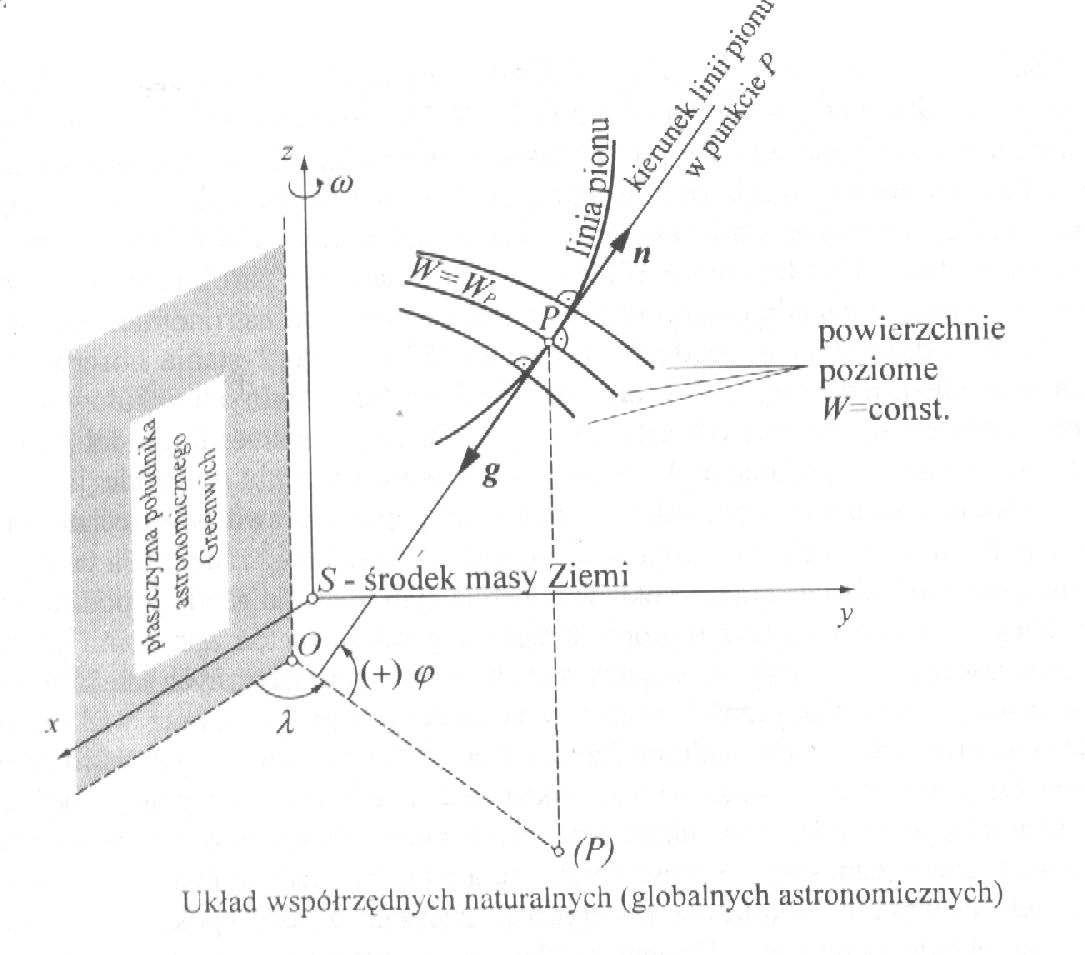
Kierunek linii pionu jest podstawą układu horyzontalnego, będącego z reguły lokalnym układem obserwacyjnym na pow. Z czyli układem który realizujemy za pomocą osi i płaszczyzn spoziomowanych instr obserwacyjnych. Związek tego układuz układem globalnym następuje poprzez tzw układ współrzędnych naturalnych. Osią układu jest chwilowa oś obrotu Z (![]()
), przechodząca przez punkt S środka masy Z. Płaszczyzna przechodząca przez pkt S i prostopadła do osi obr nazywamy płaszczyzna równika astronomicznego. Przez kier linii pionu obserw. Greenwich prowadzimy pęk płaszczyzn wertykalnych i wybieramy tę która jest równoległa do (![]()
) i nazywamy ją płaszczyzną południka astronomicznego Greenwich. Podobnie wyznacza się płaszczyznę południka w miejscu obserwacji w punkcie P.
Szerokość geograficzno - astronomiczna - kąt jaki tworzy kierunek linii pionu w pkcie P z płaszcz. równika ϕ (0o - ±90o)
Długość geograficzno - astronomiczna - kąt dwuścienny utworzony przez opisanie płaszczyzny południków astronomicznych (Greenwich i punktu P) λ(0o - 360oE lub 0o - ±180oE,W).
Kierunek linii pionu w pkcie P (g=gradWp) można określić kątami ϕ i λ wyznaczanymi met. astr. Zdefiniowane kąty i wartość potencjału W tworzą trojkę wsp. naturalnych punktu P. W polu siły ciężkości możemy wyróżnić trzy powierzchnie ϕ=const λ=const W=const których przecięcie wyznacza punkt P.
Pokaż, że średni promień krzywizny elipsoidy obrotowej jest średnią geometryczną głównych promieni krzywizny.
Na podst. wzoru Eulera ![]()
możemy wyzn średni promień krzywizny jako granicy do której dąży średnia arytmetyczna krzywizn przekrojów normalnych w rozpatrywanym pkcie. Sumę nieskończenie wielu promieni krzywizn wyznaczamy z całki, której rozwiązaniem jest średni promień krzywizny ![]()
 | Pobierz cały dokument wyzsza.gik.semestr.4.wyzsza.gw.doc rozmiar 928 KB |