PAŃSTWOWA WYŻSZA SZKOŁA ZAWODOWA INSTYTUT POLITECHNICZNY |
||||
2004/2005 |
LABORATORIUM Z AUTOMATYKI I STEROWANIA |
|||
Ćwiczenie nr 2 |
BADANIE CZŁONU CAŁKUJĄCEGO I RÓŻNICZKUJĄCEGO |
|||
Budowa i Eksploatacja Maszyn ST. Zaoczne Semestr III |
Dyksik Arnold Stefaniak Łukasz Kania Mateusz |
|||
Data wykonania |
|
Data |
Ocena |
Podpis |
2005-05-08 |
T |
|
|
|
|
S |
|
|
|
Cel ćwiczenia
Celem ćwiczenia jest zbadanie właściwości dynamicznych członów różniczkujących i całkujących opisanych następującymi transmitancjami:
![]()
- dla członu różniczkującego
![]()
- dla członu całkującego
Przebieg ćwiczenia
Badanie rzeczywistego członu różniczkującego
wymuszenie typu skok jednostkowy
Odpowiedź układu jest następująca
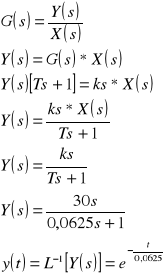
wymuszenie typu impuls jednostkowy
Odpowiedź układu jest następująca
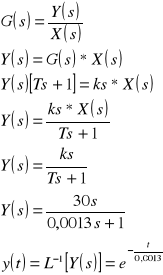
wymuszenie typu sygnał liniowo - narastający
Odpowiedź układu jest następująca
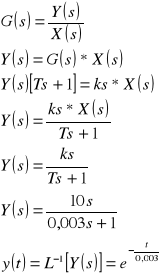
wyznaczanie charakterystyki amplitudowo-fazowej (wykres Nyquista).
Odpowiedź układu jest nastepująca
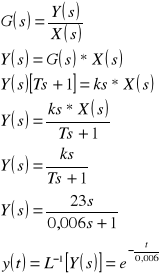
wyznaczanie charakterystyki amplitudowo-fazowej (wykres Bodego).
Odpowiedź układu jest następująca
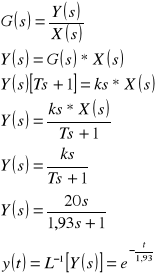
Badanie członu całkującego
wymuszenie typu skok jednostkowy
Odpowiedź układu jest następująca
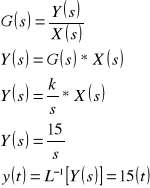
wymuszenie typu impuls jednostkowy
Odpowiedź układu jest następująca
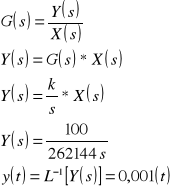
wymuszenie typu sygnał liniowo - narastający
Odpowiedź układu jest następująca
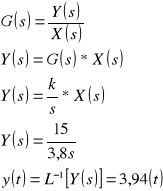
wyznaczanie charakterystyki amplitudowo-fazowej (wykres Nyquista).
Odpowiedź układu jest następująca
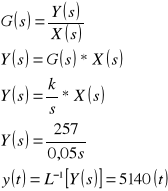
wyznaczanie charakterystyki amplitudowo-fazowej (wykres Bodego).
Odpowiedź układu jest następująca
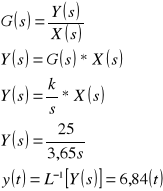
3. Wnioski
Człon całkujący - wyznacza sygnał sterujący na podstawie całki dotychczasowych wartości uchybu; jego zaletą jest to, że sprowadza uchyb ustalony do zera, bo nawet przy minimalnej wartości uchybu, w odpowiednio długim przedziale czasowym całka z tego uchybu będzie wystarczająco duża, aby wpłynąć na stan obiektu; przy odpowiednio wolnym zakłóceniu wpłynie na stan obiektu dokładniej niż człon proporcjonalny,
G(s) = ![]()
Gdzie Ti - stała czasowa całkowania
Człon różniczkujący - wyznacza sygnał sterujący na podstawie pochodnej (czyli prędkości narastania) chwilowego uchybu; oznacza to że na szybkozmienne zakłócenie zareaguje szybciej niż regulator proporcjonalny; jego zaletą jest możliwość wpływania na zmiany stanu obiektu szybciej, niż potrafiłby to zrobić człon proporcjonalny.
G(s) = ![]()
Gdzie Td - stała czasowa różniczkowania
Charakterystyki Bodego są charakterystykami logarytmicznymi. Tą nazwą obejmujemy dwie charakterystyki.
Logarytmiczna charakterystyka modułu - krzywa we współrzędnych prostokątnych, gdzie na osi odciętych odkładamy pulsację w skali logarytmicznej, a na osi rzędnych moduł M( ) transmitancji widmowej G(j ) wyrażony w decybelach odkładamy na skali liniowej
M( )|[dB] = 20 log ( |G(j )| ) = 20 log A( )
Logarytmiczna charakterystyka fazy - krzywa we współrzędnych prostokątnych, gdzie na osi odciętych odkładamy również pulsację w skali logarytmicznej, a na osi rzędnych faza ( ) w skali liniowej wyrażoną w stopniach
( ) = arg [G(j )].
Charakterystyki te łącznie w pełni opisują liniowy układ dynamiczny. Charakterystyki Bodego mają tę zaletę, iż można je łatwo przedstawić za pomocą asymptot. Taka przybliżona charakterystyka zwana charakterystyką asymptotyczną jest linią łamaną składającą się z odcinków asymptot charakterystyki rzeczywistej. Prostota polega na tym, że w transmitancjach widmowych występuje kilka typowych wyrażeń o charakterystycznym rozłożeniu zer i biegunów i można do nich stosować kilka prostych reguł.
Charakterystyka Nyquista jest wykresem transmitancji widmowej T(j)=P()+jQ() we współrzędnych zespolonych (P,Q).
W praktyce interesuje nas jedynie część wykresu charakterystyki dla pulsacji dodatnich. Strzałka na charakterystyce określa wzrost pulsacji . Z wykresu można odczytać maksimum charakterystyki amplitudowej A()=K dla pulsacji =0 oraz pulsację 1 przy której
. Dla T odczytujemy, że = - 45. Przy dążącej do nieskończoności amplituda zmierza do zera a faza do -90. Z wykresu Nyquista możemy odczytać, że =0 gdy punkt charakterystyki leży na dodatniej półosi rzeczywistej, = - 90. Amplitudę odczytujemy jako odległość danego punktu charakterystyki od środka układu współrzędnych.
Wyszukiwarka
Podobne podstrony:
człon inercyjny-laborka, mechanika, BIEM- POMOCE, automatyka i sterowanie
badanie silnika krokowego, mechanika, BIEM- POMOCE, automatyka i sterowanie
układy kombinacyjne, mechanika, BIEM- POMOCE, automatyka i sterowanie
Bramka+AND, mechanika, BIEM- POMOCE, automatyka i sterowanie, laborka ais
przerzutnik schmitta, mechanika, BIEM- POMOCE, automatyka i sterowanie, laborka ais
układ schmitta, mechanika, BIEM- POMOCE, automatyka i sterowanie, laborka ais
podst elektroniki, mechanika, BIEM- POMOCE, automatyka i sterowanie, laborka ais
Badanie członu inercyjnego I, mechanika, BIEM- POMOCE, automatyka i sterowanie
maszyny2, mechanika, BIEM- POMOCE, eksploatacja i niezawodność
układy elektroniczne-laborka, mechanika, BIEM- POMOCE, laborki elektra
ochrona środowiska, mechanika, BIEM- POMOCE
Fizyka II s. Elektrostatyka 2, mechanika, BIEM- POMOCE, laborki z fizy, moje, laboratorium z fizyki,
maszyny wirujące, mechanika, BIEM- POMOCE, eksploatacja i niezawodność
PWSZ w PILE, mechanika, BIEM- POMOCE, pkm
lab ćw3, mechanika, BIEM- POMOCE, laborki z fizy
cin2, mechanika, BIEM- POMOCE, laborki z fizy, fizyka laborki
więcej podobnych podstron