Laboratorium z metrologii elektrycznej i elektronicznej
II ELEKTR	Temat : Zastosowanie interfejsu IEC-625 do pomiaru wzorcowych konduktywności.	Data: 17.03.1998
Gr.	Arkadiusz Krzywda, Kroczak Janusz	Ocena:

Celem ćwiczenia jest pomiar konduktywności dla próbki miedzi przy użyciu cyfrowego układu pomiarowego, na który składa się układ pomiarowy analogowy, system komunikacji oraz blok programująco - sterujący, którym jest komputer.

Komunikacja układu pomiarowego z komputerem odbywa się za pośrednictwem interfejsów. Najpopularniejszym i najczęściej stosowanym jest interfejs równoległy IEC-625.

Zautomatyzowany laboratoryjny układ pomiarowy do pomiaru konduktywności jest zbudowany z urządzeń, które poprzez system interfejsu mogą komunikować się z komputerem. otrzymują one informacje o przebiegu procesu pomiaru, czyli o jego inicjacji, zmianie konfiguracji podłączeń punktów pomiarowych, końca rejestracji itp..

Układ laboratoryjny do pomiaru konduktywności:

Schemat montażowy układu do pomiaru konduktywności:

W trakcie procesu pomiaru wartości napięć UN1, UX1, UN2, UX2, są rejestrowane przez komputer. Na ich podstawie wyliczone są poszczególne wartości rezystancji i konduktancji.

Rezystancja RX1 wyliczana jest na podstawie wzoru:

gdzie:

UX1 - wartość zmierzonego napięcia na RX

UN1 - wartość zmierzonego napięcia na RN

RN - wartość oporu wzorcowego 0.001.

Rezystancja RX2 - według wzoru:

gdzie:

UX2 - wartość zmierzonego napięcia na RX

UN2 - wartość zmierzonego napięcia na RN

RN - wartość oporu wzorcowego 0.001.

Wzór na rezystancję średnią RX ma postać:

gdzie wzory na RX1 i RX2 zostały podane wyżej.

Rezystancja R20 wyliczana jest ze wzoru:

gdzie:

R20 - wartość rezystancji RX przeliczona na temperaturę 20C, w przypadku

gdy temperatura próbki w trakcie trwania pomiaru różna jest od 20C

r - temperaturowy współczynnik rezystancji.

Rezystancja średnia z n pomiarów Rśr wyliczana jest na podstawie wzoru:

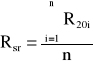
Konduktancja jednego pomiaru wyliczana jest na podstawie wzoru:

gdzie:

l - długość danej próbki

s - przekrój danej próbki.

Konduktancja średnia śr z n pomiarów wyliczona jest ze wzoru:

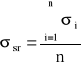
Odchylenie standardowe pomiaru rezystancji SR z n pomiarów według wzoru:

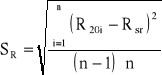
Przykładowe obliczenia sprawdzające:

Korzystając z wyżej wymienionych wzorów sprawdziłyśmy pomiar próbki miedzi.
Obliczenia wykonaliśmy dla pomiarów numer 1, 4 i 8 z pierwszej serii pomiarów, natomiast z drugiej serii - pomiary numer 1, 2 i 3.

1. Pierwsza seria (pomiar 1):

UN1 = 0.01215V UN2 = 0.01194V α = 0.00399

UX1 = 0.0083V UX2 = 0.0080V t = 24 oC

l = 0.575m s = 0.00015m2

wyliczona rezystancja RX1:

rezystancja odczytana z tabeli pomiarowej:

RX1 = 6.831310-5

wyliczona rezystancja RX2:

rezystancja odczytana z tabeli pomiarowej:

RX2 = 6.700210-5

wyliczona rezystancja RX:

rezystancja odczytana z tabeli pomiarowej:

RX = 6.765710-5

wyliczona rezystancja R20:

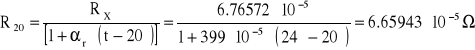
rezystancja odczytana z tabeli pomiarowej:

R20 = 6.659410-5

wyliczona konduktancja :

konduktancja odczytana z tabeli pomiarowej:

= 5.7562107 1/m

2. 
   Pierwsza seria (pomiar 4):

UN1 = 0.01213V

UX1 = 0.00081V

UN2 = 0.01219V

UX2 = 0.00084V

l = 0.575m

s = 0.00015m2

3. 
   Pierwsza seria (pomiar 8):

UN1 = 0.01214V

UX1 = 0.00081V

UN2 = 0.01207V

UX2 = 0.00083V

l = 0.575m

s = 0.00015m2

4. 
   Druga seria (pomiar 1):

UN1 = 0.01272V

UX1 = 0.00087V

UN2 = 0.01248V

UX2 = 0.00083V

l = 0.575m

s = 0.00015m2

5. 
   Druga seria (pomiar 2):

UN1 = 0.01258V

UX1 = 0.00085V

UN2 = 0.01250V

UX2 = 0.00084V

l = 0.575m

s = 0.00015m2

6. 
   Druga seria (pomiar 3):

UN1 = 0.01269V

UX1 = 0.00085V

UN2 = 0.01249V

UX2 = 0.00083V

l = 0.575m

s = 0.00015m2

WNIOSKI:

W ćwiczeniu tym pomiar rezystancji i konduktywności dla próbek miedzi
i aluminium dokonywałyśmy za pomocą zautomatyzowanego układu pomiarowego z wykorzystaniem programu komputerowego KONDUKT.EXE przeznaczonego specjalnie do tego celu.

Naszym zadaniem było tylko:

ustawienie wartości początkowych (tzn. wprowadzenie parametrów próbki i parametrów wzorca)

podanie liczby pomiarów n

załączenie źródła prądowego i napięciowego

zmiana Uk tak aby uzyskać minimalną wartość wskazywaną przez wskaźnik zera

zmiana polaryzacji.

Porównując wartości obliczone przez nas z wartościami otrzymanymi z komputera można zauważyć tylko niewielkie różnice. Różnice między pomiarami możemy zaobserwować dopiero od dziewiątego miejsca po przecinku. Jednak patrząc na wszystkie dziesięć pomiarów widać, że różnice między konduktancjami są wyraźniejsze. Może to być spowodowane niedokładnym odczytem pomiarów.

W drugiej części ćwiczenia widać, że wartości wyznaczonych konduktancji są trochę bardziej zbliżone do siebie. Również wartości konduktancji wyznaczone ze wzorów są bardziej zbliżone do konduktancji wyliczonych przez komputer.

	wyliczone	odczytane
RX1	6.6776510-5	6.677710-5
RX2	6.8908910-5	6.890910-5
RX	6.7842710-5	6.784310-5
R20	6.6777010-5	6.677710-5
	5.74049107 1/m	5.7405107 1/m

	wyliczone	odczytane
RX1	6.6721510-5	6.672210-5
RX2	6.8765510-5	6.876610-5
RX	6.7743510-5	6.774410-5
R20	6.6679310-5	6.667910-5
	5.74890107 1/m	5.7489107 1/m

	wyliczone	odczytane
RX1	6.8396210-5	6.839610-5
RX2	6.6506410-5	6.650610-5
RX	6.7451310-5	6.745110-5
R20	6.6391710-5	6.639210-5
	5.77381107 1/m	5.7738107 1/m

	wyliczone	odczytane
RX1	6.7567510-5	6.756810-5
RX2	6.7210-5	6.7210-5
RX	6.7383710-5	6.738410-5
R20	6.6325210-5	6.632510-5
	5.77960107 1/m	5.7796107 1/m

	wyliczone	odczytane
RX1	6.6981810-5	6.698210-5
RX2	6.6453110-5	6.645310-5
RX	6.6717510-5	6.671810-5
R20	6.5669410-5	6.566910-5
	5.83731107 1/m	5.8373107 1/m

I

-

-

+

+

U_n

U_x

R_n

R_x

P₂

P₁

2

1

G

V

V

Stabilizowane źródło prądu

Stabilizowane źródło napięcia

U_k

1

2

---