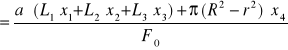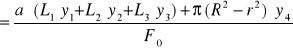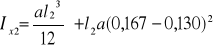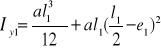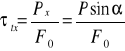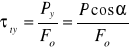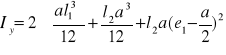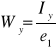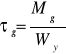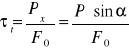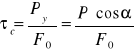DANE	OBLICZENIA I SZKICE	WYNIKI
P = 10 kN α = 75°	1. Założenia projektu Konstrukcja obciążona jest statycznie siłą P zaczepioną pod kątem α w „uchu” na końcu belki.
Materiał: St3s	2. Dobór materiału Elementy z których składa się konstrukcja wykonane są ze stali niestopowej konstrukcyjnej o oznaczeniu St4s. Wartości kr, kc, kg, ks, kt zostały odczytane z książki A.Rutkowskiego „Części Maszyn”.	kr = 120 MPa kc= kr = 120 MPa kg = 145 MPa ks = 75 MPa kt = ks = 75 MPa
H = 0,3 m g = 0,038 m h = 0,120 m b = 0,080 m l =0,4 m P = 10 kN α = 75° Wz= 2,05⋅10^-4m^3 Fo= 6,84⋅10^-3m^2 b = 0,080 m l = 0,4 m σg = 16,45 MPa σr = 0,34 MPa τt = 1,41 MPa kg = 145 MPa	3. Szkic teoretyczny 4.Obliczenia dla przekroju A-A Pole przekroju: Fo = (H-h)⋅g Wskaźnik wytrzymałości przekroju na zginanie: W układzie występuje złożony stan naprężeń (rozciąganie, zginanie, ścinanie): - moment zginający σg = σg = - naprężenie zginające σr = = σr = - naprężenie rozciągające τt = = τt = - naprężenie ścinające Dominującym naprężeniem jest zginanie. Z hipotezy wytężeniowej Hubera naprężenie zastępcze wynosi: σzast. = Porównanie naprężenia zastępczego z dopuszczalnym: σzast. < kg 17,02 MPa < 145 MPa	Fo= 6,84⋅10^-3 m^2 Wz= 2,05⋅10^-4 m^3 σg = 16,45 MPa σr = 0,34 MPa τt = 1,41 MPa σzast = 17,02MPa Materiał nie ulegnie zniszczeniu w przekroju A-A
d = 0,06 m D = 0,14 m g = 0,038 m P = 10 kN α = 75° Fo = 3,04 ⋅10^-3 m^2 σr = 0,86 MPa τt = 3,17 MPa kt = ks = 75 MPa	5.Obliczenia dla przekroju B-B Pole przekroju: Fo = g ⋅(D-d) W układzie występuje złożony stan naprężeń (rozciąganie, ścinanie): σr = = σr = - naprężenie rozciągające τt = = τt = - naprężenie ścinające Dominującym naprężeniem jest ścinanie. Z hipotezy wytężeniowej Hubera naprężenie zastępcze wynosi: τzast. = Porównanie naprężenia zastępczego z dopuszczalnym τzast. < kt 3,21 MPa < 75 MPa	Fo = 3,04 ⋅10^-3m^2 σr = 0,86 MPa τt = 3,17 MPa τzast. = 3,21 MPa Materiał nie ulegnie zniszczeniu w przekroju B-B

a = 0,026 m L1= 0.400 m L2= 0,300 m L3= 0,400 m R = 0,06 m r = 0,05 m O1=(0,226; 0,339) O2=(0,013; 0,176) O3=(0,226; 0,013) O4=(0,226; 0,176) a = 0,026 m L1= 0.400 m L2= 0,300 m L3= 0,400 m R = 0,06 m r = 0,05 m e1=0.141 e2=0.259 Ix= 2,44* 10^-^4 cm^4 Iy=33,97* 10^-^4cm^4 P = 10 kN α = 75° Fo = 32,7 ⋅10^-3 m^2 τtx = 0,08 MPa τty = 0,3 MPa r1 = 0,25 m r2 = 0,31 m r3 = 0,28 m r4 = 0,20 m I0 =3,64⋅ 10^-3m^4 W01=14,56⋅10^-3m^3 W02=11,74⋅10^-3m^3 W03=13,01⋅10^-3m^3 W04=18,21⋅10^-3m^3 Ms= 4760 Nm τwyp=0,53 MPa kt= 75 MPa	6. Sprawdzanie wytrzymałości spoiny pachwinowej: a=0,7⋅g=0,026 m Przekrój obliczeniowy: Fo=a⋅(L1+L2+L3+L4)+Π⋅(R^2-r^2) 6a. Współrzędne środków ciężkości poszczególnych części spoiny pachwinowej: O1=(0,226; 0,339) O2=(0,013; 0,176) O3=(0,226; 0,013) O4=(0,226; 0,176) 6b. Wyznaczanie środków ciężkości dla całej spoiny pachwinowej: = 6c. Obliczenie momentów bezwładności spoiny pachwinowej: 6d. Biegunowy moment bezwładności: I0 = Ix + Iy 6e. Wyznaczenie naprężenia ścinającego od siły P: τt obliczam z Twierdzenia Pitagorasa: 6f. Wyznaczanie momentu skręcającego działającego na spoinę: Ms = Px(b+0,046) + Py(l+0,059)= P⋅sinα(b+0,046) + P⋅cosα(l+0,059) 6g. Wskaźniki wytrzymałościowe na skręcanie: 6h. Wyznaczanie naprężeń skręcających: 6i. Wyznaczanie naprężenia wypadkowego: Metoda graficzna Skala: 1:10 Skala sił: 1 [mm]-1 MPa Zgodnie z rysunkiem: τs2 = 0,41 MPa τt = 0,31 MPa Wyznaczona (na podstawie sumy wektorowej )na rysunku wypadkowa τ zgodnie z podaną wyżej skalą ma wartość τ= 0,72 MPa 6j. Porównanie naprężenia wypadkowego z naprężenie dopuszczalnym: τwyp. ≤ 0,65 kt 0,72 MPa ≤ 48,75 MPa	Fo = 32,7 ⋅10^-3 m^2 Xc = 0,167 m Yc = 0,130 m Ix1=0,02 ⋅ 10^-4cm^4 Ix2=0,7 ⋅ 10^-4cm^4 Ix3=1,45 ⋅ 10^-4cm^4 Ix4=0,25 ⋅ 10^-4cm^4 Ix =2,44 ⋅10^-4 cm^4 Iy1=1,79 ⋅ 10^-4cm^4 Iy2=10,89⋅10^-4cm^4 Iy3=16,4 ⋅ 10^-4cm^4 Iy4= 4,9 ⋅10^-4cm^4 Iy=33,97 ⋅10^-4cm^4 I0 = 3,64 ⋅ 10^-3m^4 τtx = 0,08 MPa τty = 0,3 MPa τt = 0,31 Mpa Ms= 4760 Nm W01=14,56⋅10^-3m^3 W02=11,74⋅10^-3m^3 W03=13,01⋅10^-3m^3 W04=18,21⋅10^-3m^3 τs1 = 0,33 MPa τs2 = 0,41 MPa τs3 = 0,37 MPa τs4 = 0,26 MPa Spoina pachwinowa wytrzyma dane naprężenia
P = 10 kN α = 75° Β = 30° g = 0,038 m l0 = 0,227 m z1=0,093 m z2=0,023 m g = 0,038 m l0 = 0,227 m P = 10 kN α = 75° Β = 30° Fo = 8,6 ⋅10^-3 m^2 Wx=3,26⋅10^-4m^3 z1=0,093 m z2=0,023 m σr = 1,06 MPa τt = 0,47 Mpa σg = 1,79 MPa kg = 145 MPa σzast =2,97 MPa	7. Sprawdzanie wytrzymałości spoin - spoina czołowa Przekrój obliczeniowy spoiny: Fo = lo ⋅ g Wskaźnik wytrzymałości przekroju na zginanie: W układzie występuje złożony stan naprężeń (zginanie, rozciąganie, ścinanie): σr = = σr = - naprężenie rozciągające τt = = τt = - naprężenie ścinające - moment zginający σg = σg = - naprężenie zginające Dominującym naprężeniem jest zginanie. Z hipotezy wytężeniowej Hubera naprężenie zastępcze wynosi: σzast. = Porównanie naprężenia zastępczego z dopuszczalnym: σzast. < 0,9 kg 2,97 MPa < 130,5 MPa	Fo = 8,6 ⋅10^-3 m^2 Wx=3,26⋅10^-4m^3 σr = 1,06 MPa τt = 0,47 Mpa σg = 1,79 MPa σzast =2,97 MPa Spoina czołowa wytrzyma dane naprężenia
l1= 0,6 m l2 = 0,038m a = 0,026 m e1= 0,326 m e2= 0,326 m l1= 0,6 m l2 = 0,038 m a = 0,026 m e1= 0,326 m e2= 0,326 m Iy=1,156⋅10^-3m^3 e1= 0,326 m P = 10 kN α = 75° h=0,480 m l=0,500 m Mg = 6,08 kNm Wy=3,5⋅10^-3m^3 F0=0,0339 m^2 τg=1,72MPa τt=0,08 MPa τc=0,28 MPa τz=2,00MPa kr = 120 MPa kc= kr	8. Sprawdzenie spoiny pachwinowej przy podstawie Przekrój obliczeniowy: F0=2al1+2al2=2a(l1+l2) 8a. Moment bezwładności spoiny pachwinowej: e1=e2 8b. Wskaźnik wytrzymałości przekroju na zginanie: Mg=Py⋅l+Px⋅h=Pcosα⋅l+Psinα⋅h 8c. Naprężenie zginające: 8d. Naprężenie ścinające: 8e. Naprężenie ściskające: 8f. Wyznaczenie naprężenia zastępczego: Porównanie naprężenia zastępczego z dopuszczalnym: τz < 0,65 kr 2,00 MPa < 78 MPa	F0=0,0339 m^2 Iy=1,156⋅10^-3m^3 Wy=3,5⋅10^-3m^3 Mg = 6,08 kNm τg=1,72 MPa τt=0,08 MPa τc=0,28 MPa τz=2,00MPa Spoina pachwinowa przy podstawie wytrzyma dane obciążenie.
	9. Wnioski: Na podstawie przeprowadzonych wyżej obliczeń można stwierdzić, iż dana konstrukcja o dobranych wymiarach i dobranym materiale przeniesie zadane obciążenie P=10 kN i nie ulegnie zniszczeniu.

POLITECHNIKA ŚLĄSKA W GLIWICACH WYDZIAŁ TRANSPORTU W KATOWICACH

PODSTAWY KONSTRUKCJI MASZYN

PROJEKT numer 1

Temat : Połączenia spawane

Wykonał:

Sienkiewicz Patryk

T36 LT

10

L₃

P

L₁

L₂

---