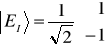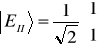Temat: Inny przykład układu o dwóch stanach: cząstka amoniaku

Konstrukcja macierzy Hamiltona dla cząstki amoniaku

Chemicy ustalili, że cząstka amoniaku zbudowana jest z jednego atomu azotu i trzech atomów wodoru. Jego formuła chemiczna to NH₃. Ustalono, że cząstka ta ma kształt piramidy. W jej podstawie znajdują się atomy wodoru. Atom azotu może się znajdować w dwóch stanach - poniżej i powyżej podstawy. Oprócz tego cała cząstka amoniaku może poruszać się ruchem postępowym i obracać się, a atomy z której jest ona zbudowana mogą drgać dookoła położeń w wierzchołkach piramidy. Założymy, że molekułę
nie działają zewnętrzne pola.

Rys. 11.1

Niech π będzie płaszczyzną, w której leżą atomy wodoru. Jak powiedzieliśmy atom azotu N może znajdować się pod płaszczyzną π albo nad nią. Cząstka
porusza, obraca się i drga. Niech parametr s charakteryzuje wszystkie ruchy oprócz zmiany położenia atomu azotu względem płaszczyzny π. Będziemy zajmowali się jedynie położeniem atomu azotu względem tej płaszczyzny. Dlatego przyjmiemy, że parametr s jest ustalony. Umówimy się, że pierwszym stanem molekuły amoniaku jest „atom N nad π”, a drugim „atom N pod π” Możliwe są tylko dwa położenia atomu azotu - dwa jego stany. Dlatego dwa wektory stanu
,
tworzą bazę fizyczną pozwalającą opisać tę własność cząstki azotu do której ograniczyliśmy się. Dowolny wektor stanu cząstki amoniaku w momencie czasu t można zapisać w postaci superpozycji

. (11.1)

Zbudujemy operator Hamiltona badanego układu kierując się różnego rodzaju wskazówkami. Niech O będzie obserwatorem znajdujący się nad π, natomiast O^/ - obserwatorem znajdują­cym się pod π. Przyjmijmy, że obserwator O widzi molekułę
w stanie określonym przez wektor
. Wtedy obserwator
widzi ją w stanie
. Ponieważ nie istnieje wyróżniony zwrot osi prostopadłej do płaszczyzny π, wyniki pomiarów wykonane przez O i
nie mogą się różnić.

W bazie wektorów stanu
operator
reprezentuje macierz
o elementach

,
,
,
. Ponieważ operator
musi być hermitowski więc elementy macierzowe spełniają związki

,
,
. (11.2)

Niediagonalne elementy operatora Hamiltona określają przejścia pomiędzy stanami
i
. Ponieważ
macierz H może zależeć od czterech parametrów (
). Jednak nie wszystkie one muszą być niezależne. Będziemy się starali zmniejszyć liczbę niezależnych parametrów.

Niech
będzie operatorem odpowiadającym przekształceniu odbiciu w płaszczyźnie π. Będziemy go nazywali operatorem odbicia. Działając na wektory stanu molekuły azotu operator przeprowadza jeden wektor w drugi

,
. (11.3)

W bazie wektorów stanu
elementy macierzowe operatora odbicia znikają

,
. (11.4a,b)

Natomiast nie znikają elementy niediagonalne

,
. (11.4c,d)

Zatem operator odbicia w bazie wektorów
reprezentuje macierz

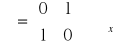
. (11.5a)

Macierz
jest jedną z macierzy Pauliego. Podobnie jak macierz
(8.7b) macierz
spełnia związek

. (11.5b)

Z definicji operatora odbicia wynika, że

,
,

a więc

. (11.6)

Podkreślmy - wektory
nie są wektorami własnymi operatora odbicia. Diagonalne elementy macierzy H nie mogą się różnić, bo element macierzowy, który obserwator O uważa za
obserwator O^/ uważa za
, więc

. (11.7a)

Na podstawie podobnego argumentu, stwierdzamy, że

. (11.7b)

Zatem w bazie stanów
operator Hamiltona reprezentuje macierz o bardzo prostej strukturze

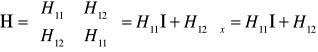
. (11.8)

Ponieważ macierz reprezentująca hamiltonian nie jest diagonalna więc wektory
nie są jej wektorami własnymi.

Pokażemy, że operator Hamiltona komutuje z operatorem odbicia. W tym celu rozpatrzymy elementy macierzowe
. Mamy

.

Na podstawie relacji (11.7a) stwierdzamy, że

. (11.9a)

Podobnie

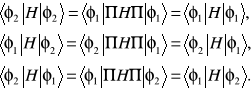
Jak widać słuszna jest relacja

.

Po pomnożeniu jej z lewej albo z prawej strony przez operator odbicia stwierdzamy, że
, albo

. (11.10)

O operatorze komutującym z hamiltonianem mówimy, że jest całką ruchu. Operator odbicia jest całką ruchu. Zdaje ona przekształcenie dyskretne, dlatego nie jest związana z jakim­kol­wiek generatorem.

11.2 Wartości własne i wektory własne hamiltonianu molekuły amoniaku

Za Feynmanem [1] wprowadzimy oznaczenia

.

Znajdziemy wektory własne i wartości własne macierzy H. Przyjmiemy, że dwa wektory własne w bazie
mają składowe a_γ, b_γ (
). Powinniśmy rozwiązać równanie

.

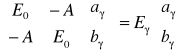
Nietrudno znaleźć wartości własne

. (11.12a,b)

Jak widać dopuszczalnymi wartościami energii
są
- jest ona kwantowana. Składowe
wektorów własnych są proporcjonalne

. (11.12c)

Podstawiając do wzoru (11.12c) wyrażenie dla E_I (11.12a) otrzymamy
, natomiast dla E_II (11.12b) otrzymamy
. Teraz już możemy podać postać wektorów własnych

,
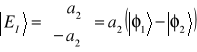
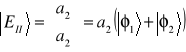
. (11.13a,b)

Powinny być one ortogonalne
i unormowane do jedności
. Z ostatniego warunku wynika, że
. Wektory własne i wartości własne operatora
zebraliśmy w Tabeli 11.1

Γ	Wektor własny	Wartość własna	Wartość własna
I			-1
II			1

Tabela 11.1

Gdy
, tj. gdy
, mamy do czynienia z parą niezależnych równań

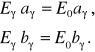
Wartości własne
są jednakowe
. Mówimy wtedy o zwyrodnieniu widma energii. Gdy stopniowo będziemy powiększać parametr A od zera do skończonej wartości A to dwa początkowo zwyrodniale poziomy energii stopniowo będą się rozsuwać, mówimy wtedy o ich rozczepieniu. Dla
różnica energii poziomów E_II i E_I wynosi 2A (Rys. 11.2). W bazie stanów
macierz Hamiltona nie jest diagonalna, pozadiagonalne wyrazy
związane są z przejściem układu ze stanu
w
i odwrotnie. By podkreślić kwantową naturę tych przejść będziemy mówili o tunelowaniu atomu azotu z konfiguracji 1 do konfiguracji 2 i o procesie odwrotnym. Gdy pozadiagonalne elementy macierzowe znikają takich przejść nie ma. Tunelowanie powoduje rozczepienie (usunięcie zwyrodnienia) poziomów energii układu. Jest to wniosek ogólny, słuszny nie tylko dla cząstki amoniaku.

Rys. 11.2

Zbadajmy jak działa operator odbicia na wektory własne hamiltonianu. Po uwzględ­nieniu związku (11.3) otrzymamy

,
. (11.14a,b)

Wektorowi
odpowiada wartość własna (-1), natomiast
- wartość własna (+1). Jak widać wektor
jest nieparzysty, zaś wektor
jest parzysty względem operacji odbi­cia. Parzystość
jest liczbą kwantową pozwalającą klasyfikować stany cząstki amoniaku. Stany o energiach
mają określoną parzystość. Natomiast stany
nie są stanami o określonej parzystości. Dla nich parzystość
nie jest dobrą liczbą kwantową. W reprezentacji stanów I i II macierze operatorów są diagonalne

,
.

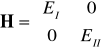
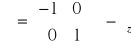
Macierz
spełnia związek (11.5b). Macierze Pauliego
nie komutują.

Zauważymy, że reprezentacji energii kwadrat macierzy
także spełnia warunek (11.6). Gdy we wzorze (11.8) zapiszemy macierz
w reprezentacji energii to otrzymamy diagonalną postać macierzy
, zatem

. (11.15)

11.3 Ewolucja wektorów stanu cząstki amoniaku z upływem czasu

Zajmijmy się ewolucją wektorów stanu

. Przyjęliśmy, że na cząstkę tę nie działają pola zewnętrzne, więc hamiltonian nie zależy od czasu. Dlatego operator ewolucji
ma prostą postać (10.31)

.

Ponieważ operator ewolucji jest funkcją hamiltonianu, więc także komutuje z operatorem odbicia

. (11.16)

Zbadajmy wynik działania operatora odbicia na wektor

.

Stwierdzamy więc, że możemy poddać operacji odbicia wektor
albo poddać tej operacji wektor początkowy, a następnie tak przekształcony wektor poddać ewolucji w ciągu interwału czasowego (t₀, t). Wynik będzie ten sam. Ta własność jest konsekwencją symetria układu nie ulega zmianie w czasie ewolucji.

11.4 Rozwiązanie równania Schródingera

Zajmijmy się teraz rozwiązaniem równania Schrödingera. Niech
będzie początkowym wektorem stanu, a
- wektorem stanu w momencie czasu t. Dla amplitud
wprowadzimy specjalne oznaczenie
. Amplitudy te spełniają równanie Schrödingera

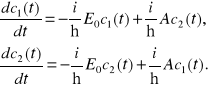
. (11.17a,b)

Będziemy szukać rozwiązań postaci

. (11.18a)

Uzasadnimy ją później. Dla tej postaci współczynników równanie różniczkowe zamienia się w równanie algebraiczne

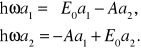
Te ostatnie równania nie różnią się od równań na wartości i wektory własne macierzy H (11.8). Zatem

,
. (11.19a,b)

Ostatecznie

. (11.18b)

11.4 Ewolucja stanu cząstki amoniaku z upływem czasu

Zbadamy zachowanie się rozwiązań równania Schrödingera z upływem czasu. Przyjmiemy, że rozpoczęliśmy obserwację w momencie czasu
. Ponieważ hamiltonian nie zależy od czasu więc, wyniki nie zależą od wyboru momentu początku odczytu czasu. Ponownie oprze­my się na zasadzie superpozycji

. (11.20)

Zajmijmy się amplitudą prawdopodobieństwa
zdarzenia polegającego na tym, że cząstka amoniaku będąca w stanie
zachowuje się jak gdyby była w stanie o energii
. Ponieważ wektor bra
jest także wektorem własnym hermitowskiego operatora Hamiltona

, (11.21)

a to jest postać (11.16).

Jawna zależność od czasu amplitud
zależy od wyboru stanu początkowego. Aby zrozumieć ten wpływ rozpatrzymy przykład. Niech
. Obliczymy odpowiednie amplitudy

. (3.22a,b)

Jak widać dla wybranego przez nas stanu początkowego

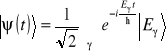
. (3.23)

Ustalimy zależność od czasu amplitudy
i prawdopodobieństwa
znalezienia układu po czasie t w stanie

,

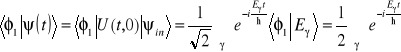
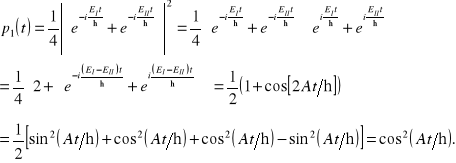
(11.24a)

Podobnie

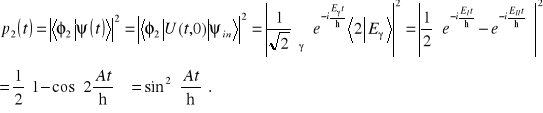
(11.24b)

Rzecz jasna, w każdym momencie t czasu suma prawdopodobieństw
,
równa jest jedności.

Pokażemy, że prawdopodobieństwa
,
można otrzymać na innej, bardziej formalnej drodze. Zauważymy, że zgodnie ze wzorem (11.15) operator Hamiltona można przedstawić w postaci kombinacji liniowej dwóch operatorów
, a operator
spełnia warunek (11.6). Przedstawimy operator ewolucji
w postaci szeregu potęgowego, który podobnie jak w przypadku operatora ewolucji (10.24) podzielimy na dwie części. Oto ostateczny wynik

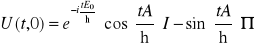
. (11.25)

Zbadajmy jak operator ewolucji zmienia wektor
, zauważymy przy tym, że dla przyjętego warunku początkowego wynik działania operatora
na
jest stanem

.

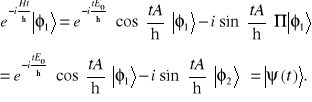
Nietrudno znaleźć elementy macierzowe

,
,

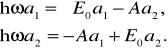
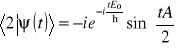
a więc także i prawdopodobieństwa

.

Wykres zależności prawdopodobieństw od czasu przedstawia Rys. 11.3

Rys.11.3

Gdy układ znajduje się w stanie stacjonarnym, tj. w jednym ze stanów własnych operatora energii to zgodnie ze wzorem (10.40) zawsze w takim stanie pozostanie i odpowiednie prawdopodobieństwo nie zależy od czasu.

11.5 Iloczyn prosty wektorów stanu

Jak powiedzieliśmy atom azotu N może znajdować się pod płaszczyzną π (w stanie 1) albo nad nią (w stanie 2). Oprócz tego cząstka
ma jeszcze inne stopnie swobody - bo cała może się poruszać i obracać się, dodatkowo atomy całej cząstki w skoordynowany sposób drgają wokół położeń równowagi w wierzchołkach piramidy. Jeżeli te ruchy są niezależne, tj. jeżeli słabo albo w ogóle na siebie nie wpływają, to każdy z nich określają odpowiednie, niezależne od pozostałych parametry. Inaczej mówiąc każdy z tych parametrów przyjmuje odpowiednie wartości niezależnie od wartości parametrów charakteryzujących pozostałe stopnie swobody. Z niezależnymi stopniami swobody związane są operatory, które działają na wektory stanu numerowane wartościami parametrów charakteryzujących te stopnie swobody. Te wektory stanu należą do podprzestrzeni liniowych. Położenie środka masy cząstki charakteryzuje wektor
. Nasza cząstka może się znajdować w punkcie przestrzeni r i znajdować się w stanie 1 albo 2. Stan cząstki
określa wektor stanu
, który jest iloczynem prostym (iloczynem tensorowym) wektorów stanu
i

.

Najczęściej zapisujemy iloczyn prosty pomijając znak
:
.

Przyjmijmy, że w ogólnym przypadku mamy do czynienia z N przestrzeniami
. Wprowadzimy iloczyn tensorowy wektorów (po jednym z każdej przestrzeni)

takie, że dla każdego
i dowolnych dwóch wektorów
należących do

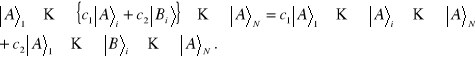
(11.26)

Zbiór wektorów
tworzy przestrzeń liniową
nazywaną iloczynem tensorowym przestrzeni
. Rozpatrzymy iloczyn skalarny dwóch wektorów

. (11.27)

Z założenia w każdej z przestrzeni

istnieje zupełny, ortonormalny zbiór wektorów
. Zbiór iloczynów tensorowych tych wektorów tworzy bazę w przestrzeni
.

Niech operator
działa na wektory stanu w przestrzeni
. W przestrzeni
odpowiada mu operator

, (11.28)

który działa na wektory należące do
w następujący sposób

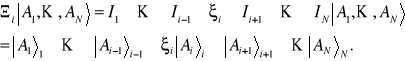
(11.29)

Operatory działające w
są sumami i iloczynami takich operatorów. Operatory
, które działają w różnych przestrzeniach, związane są z różnymi, niezależnymi stopniami swobody, komutują

. (10.30)

Tak skonstruowane przestrzenie i operatory są szczególnie przydatne w opisie układów wielu cząstek.

W szczególnym przypadku cząstki amoniaku wektor stanu
można przedstawić w postaci
, gdzie wektor
związany jest z wszystkimi pozostałymi stopniami swobody i też jest iloczynem tensorowym.

11.6 Komutujące obserwable

Literatura

[1] R.P. Feynman, R.B. Leighton, M. Sands, Feynmana wykłady z fizyki, Warszawa, PWN, 1972, R. 9.

[2] Z. Opial, Algebra Wyższa, PWN, Warszawa, 1967, R. XIII, § 2

[3] B.W. Medwedew, Naczała teoreticzeskoj fiziki, Nauka, Moskwa, 1977, § 10.81.

1

Szukasz gotowej pracy ?

To pewna droga do poważnych kłopotów.

Plagiat jest przestępstwem !

Nie ryzykuj ! Nie warto !

Powierz swoje sprawy profesjonalistom.

---