POLITECHNIKA CZĘSTOCHOWSKA

Laboratorium z

Elektrotechniki Teoretycznej

Ćwiczenie nr 3

Temat : Linia długa.

Wykonali:

Radosław Urbańczyk

Piotr Janikowski

Piotr Szelag

1. Cel ćwiczenia.

Celem ćwiczenia jest doświadczalne zapoznanie się ze zjawiskami falowymi zachodzącymi w modelu linii długiej, przy różnych obciążeniach.

2. Spis przyrządów.

- woltomierz cyfrowy V 531

- model linii długiej

- generator drgań sinusoidalnych

3. Układy pomiarowe.

a) Schemat jednego ogniwa układu zastępczego linii długiej.

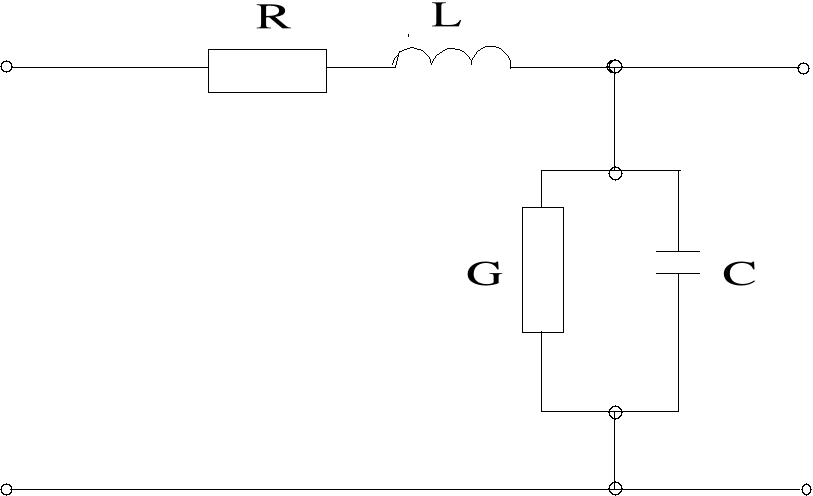
b) Schemat połączeń układu do pomiaru fali napięciowej modelu linii długiej.

4. Tabele pomiarowe.

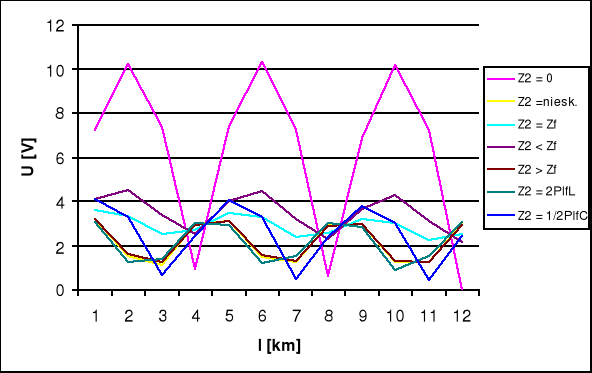
1. Rozkład napięcia wzdłuż linii długiej.

Lp.	U[V] dla f=350 Hz
		Z2 = 0	Z2 = *	Z2 = Zf	Z2 < Zf	Z2 > Zf	Z2 = 2*fL	Z2 = 1/2*fC
1	7,24	3,25	3,63	4,1	3,25	3,1	4,1
2	10,24	1,54	3,34	4,54	1,66	1,24	3,27
3	7,36	1,13	2,51	3,36	1,24	1,41	0,68
4	0,96	2,97	2,72	2,53	2,95	3,06	2,48
5	7,42	3,12	3,48	3,98	3,11	2,96	4,03
6	10,3	1,51	3,26	4,48	1,6	1,2	3,27
7	7,22	1,23	2,4	3,22	1,29	1,52	0,49
8	0,64	2,92	2,56	2,33	2,88	3,03	2,39
9	6,91	3	3,21	3,64	2,97	2,85	3,83
10	10,16	1,24	3,03	4,27	1,31	0,92	3,02
11	7,21	1,23	2,28	3,11	1,25	1,53	0,42
12	0	2,98	2,49	2,18	2,93	3,09	2,46

2. Zmiana napięcia w funkcji częstotliwości.

f [Hz]	Zacisk nr 6			Zacisk nr 12
		Z2 = 0	Z2 = *	Z2 = Zf	Z2 = 0	Z2 = *	Z2 = Zf
200	0,41	1,01	0,72	0,003	1,03	0,63
400	0,39	2,02	0,65	0,003	1,65	0,46
600	0,31	1,73	0,6	0,003	1,11	0,35
800	0,76	0,24	0,41	0,003	0,27	0,18
1000	0,004	0,004	0,004	0,003	0,003	0,003
1100	0,003	0,003	0,003	0,003	0,003	0,003

5. Wykresy charakterystyk.

1. Wykresy amplitudy w funkcji odległości U=f(l) od początku linii.

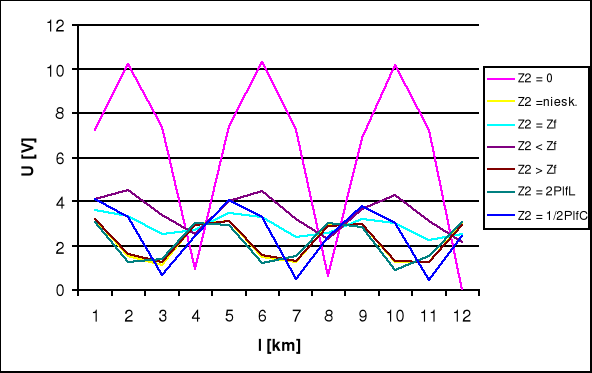
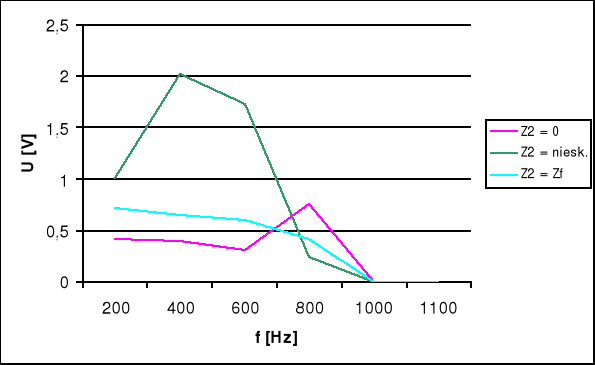
2. Charakterystyka napięciowo-częstotliwościowa U = f ( f ) w połowie długości linii.

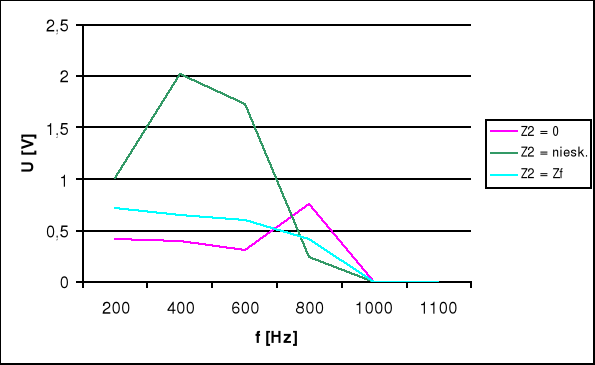
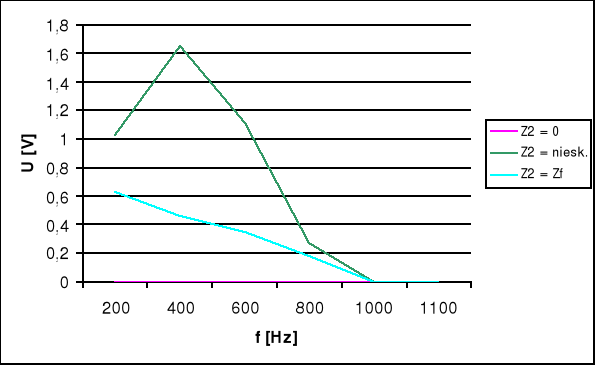
c) Charakterystyka napięciowo-częstotliwościowa U=f(f) na końcu linii.

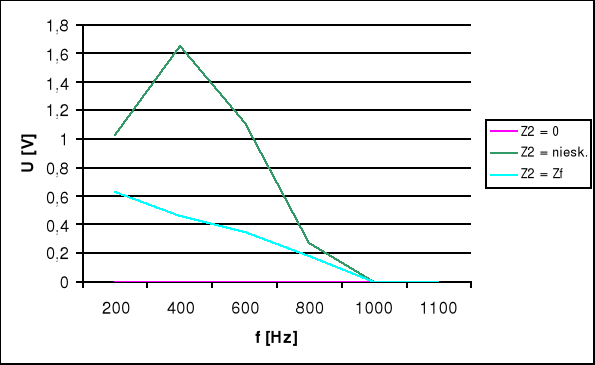
6. Obliczenia i wnioski

a) Wyprowadzenie zależności napięcia i prądu w funkcji odległości x od początku linii.

Do rozważań teoretycznych najłatwiej całą linię długą podzielić na elementarne sekcje o długości ∧x, których schemat ogólny zawiera powyżej wymienione parametry jednostkowe.

Rysunek w części teoretycznej. Wartości chwilowe prądów i napięć są funkcjami dwóch zmiennych: odległości - x i czasu - t. Korzystając z bilansu napięć w oczku można zapisać równania:

u(x,t) = R_o ∧x i(x,t) + L_o ∧x ( δi(x,t) / δt ) + u(x+∧x,t)

i(x,t) = G_o ∧x u(x+∧x,t) + C_o x ( δu(x+∧x,t) / δt ) + i(x+∧x,t)

Po przekształceniu otrzymujemy:

- (δu / δx) = R_o i + L_o (δi / δt)

-(δi / δx) = G_o u + C_o (δu / δt)

Równania te noszą nazwę równań telegrafistów.

Wartość napięcia i prądu w funkcji x (od początku linii) opisana jest równaniami:

U = U₁ ch γ x - I₁ sh γ x

I = (U₁ / Z_f ) sh γ x + I₁ ch γ x

a dla określenia napięcia i prądu w funkcji x od końca linii przyjmujemy:

x = l ; U = U₂ ; I = I₂ i równania przyjmują postać:

U = U₂ ch γ x + Z_f I₂ sh γ x

I = (U₂ / Z_f ) sh γ x + I₂ ch γ x

Podstawiając x=l ; U=U₁ ; I=I₁ obliczamy impedancję wyjściową

Z_we = (U₁ / I₁ ) = Z_f { [ (Z₂/Z_f) + th γ l ] / [ (Z₂/Z_f) th γ l + 1 ] }

i stąd otrzymujemy:

Z_{we 0} = Z_f th γ l

Z_{we ∞} = Z_f cth γ l

b) Wyprowadzenie wzorów dla linii bezstratnej.

Linia długa bezstratna w rzeczywistości nie istnieje. Jednak przyjmuje się, że dla

R_o << ω L_o i G_o << ω C_o można ją rozpatrywać jako bezstratną. Przyjmując R_o = 0

i G_o = 0 otrzymamy:

Z_c = =

γ = = jω

stąd dla linii bezstratnej :

α = 0

β = ω

i równanie napięcia i prądu f funkcji x od początku linii:

U(x) = U₁ cos β x - j Z_c I₁ sin β x

I(x) = I₁ cos β x - j (U₁/Z_c) sin β x

c) Obliczenia parametrów linii przy założeniu, że jest bezstratna.

G_o = (R_o/L_o) C_o = 50 μS/km

Z_c = = 360.5 *

n

n'

n-1

(n-1)'