Cel ćwiczenia

• Zapoznanie się ze sposobem pomiaru amplitudy i faz poszczególnych harmonicznych przebiegów niesinusoidalnych.

• Praktyczna realizacja pomiaru współczynnika zawartości harmonicznych przebiegów niesinusoidalnych.

• Doświadczalne potwierdzenie wpływu indukcyjności i pojemności na wyższe harmoniczne.

Część 1 - Pomiar amplitudy i fazy harmonicznych przebiegów niesinusoidalnych.

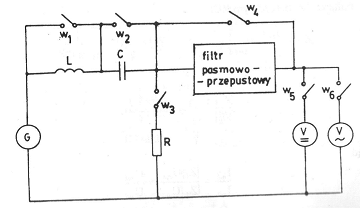
Rysunek 1 - Układ pomiarowy

W tej części ćwiczenia naszym zadaniem był pomiar wartości skutecznej (za pomocą miernika) oraz wartości maksymalnej (odczytywanej na oscyloskopie) harmonicznych przebiegów niesinusoidalnych, które zostały dostarczone przez generator o częstotliwości podstawowej równej 100 Hz. Porównywanie przebiegów podstawowych z poszczególnymi harmonicznymi pozwala na określenie fazy początkowej tych harmonicznych.

Podczas pierwszej części ćwiczenia do układu pomiarowego są dołączone dwa woltomierze oraz opór R, zaś elementy L i C na wejściu układu są zwarte. Kanał A oscyloskopu dołączyliśmy do wyjścia generatora, a kanał B do wyjścia pomiarowego układu. Następnie podawaliśmy odpowiedni sygnał na wyjściu filtru pasmowo-przepustowego. Aby otrzymać odpowiednią harmoniczną na wyjściu filtra pasmowo-przepustowego musieliśmy wybrać odpowiedni zakres częstotliwości przepuszczanych przez filtr, a potem pokrętłem regulacyjnym ustawić częstotliwość przepuszczania filtru równą dokładnie częstotliwości badanej harmonicznej, która odpowiada maksymalnemu wskazaniu woltomierza. Dla badanego przebiegu mierzyliśmy wartości skuteczne i maksymalne wszystkich harmonicznych, których częstotliwości mieszczą się w możliwych do uzyskania zakresach przepuszczania filtru. Fazy początkowe badanych harmonicznych odczytywaliśmy na ekranie oscyloskopu przez porównanie z przebiegiem podstawowym. Wyniki pomiarów zamieściliśmy w tabeli 1.

Tab.1 Wartości napięć harmonicznych dla przebiegu trójkątnego i prostokątnego

			Wartości odczytane z miernika i oscyloskopu		Wartości obliczone
Przebieg			Trójkątny	Prostokątny	Trójkątny	Prostokątny
Wartość maksymalna		V	7	5,8	7	5,8
Składowa stała		V	0	0	0	0
Wartości maksymalne harmonicznych	1	V	5,4	7,2	5,68	7,39
		2	V	-	-	-	-
		3	V	0,36	2,2	0,63	2,463
		4	V	-	-	-	-
		5	V	0,034	0,9	0,23	1,48
		6	V	-	-	-	-
		7	V	Nie udało się odczytać	0,5	-	1,06
		8	V	-	0,19	-	0
		9	V
	Wartości skuteczne harmonicznych	1	V			4,02	5,23
		2	V			-	-
		3	V			0,45	1,74
		4	V			-	-
		5	V			0,163	1,05
		6	V			-	-
		7	V			0,082	0,75
		8	V
		9	V
	Wartości początkowe harmonicznych	1		0^0	0^0
		2		-	-	-	-
		3		180^0	0^0
		4		-	-	-	-
		5		0^0	0^0
		6		-	-	-	-
		7			0^0
		8			-	-	-
		9			0^0

Podstawowe wzory i przykłady obliczeń:

• Przebieg trójkątny w postaci przebiegu Fouriera:

F(ωt)=
[sin(ωt) +
sin (3ωt) +
sin(5ωt) + … +
sin (kωt)]

• Przebieg prostokątny w postaci przebiegu Fouriera:

F(ωt)=
[sin(ωt) +
sin(3ωt) +
sin(5ωt) + … +
sin(kωt)]

• Obliczanie napięcia maksymalnego U_maxdla przebiegu trójkątnego:

W przypadku pierwszej harmonicznej:

• Obliczanie napięcia maksymalnego U_max dla przebiegu prostokątnego:

W przypadku pierwszej harmonicznej:

• Obliczanie napięcia skutecznego U_sk dla przebiegu trójkątnego:

W przypadku pierwszej harmonicznej:

• Obliczanie napięcia skutecznego U_sk dla przebiegu prostokątnego:

W przypadku pierwszej harmonicznej:

• Obliczamy wartości maksymalne kolejnych harmonicznych dla przebiegu trójkątnego:

• Obliczamy wartości maksymalne kolejnych harmonicznych dla przebiegu prostokątnego:

• Obliczamy wartości skuteczne kolejnych harmonicznych dla przebiegu trójkątnego:

• Obliczamy wartości skuteczne kolejnych harmonicznych dla przebiegu prostokątnego:
  

Część 2 - Pomiar współczynnika zawartości harmonicznych przebiegów niesinusoidalnych.

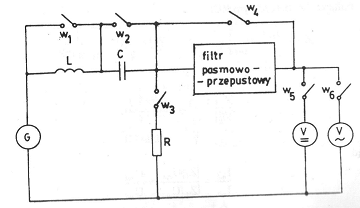
Rysunek 2 - Układ pomiarowy

Pomiar współczynnika zawartości harmonicznych wykonywaliśmy za pomocą miernika zniekształceń nieliniowych.

Na samym początku podłączony został miernik zniekształceń nieliniowych do wyjścia generatora. Następnie podawaliśmy kolejne badane przebiegi, mierząc współczynnik zawartości harmonicznych. Oprócz tego w tabelce 2 zamieściliśmy wartość skuteczną, a także składową stałą.

Tab.2 Pomiar współczynnika zawartości harmonicznych

Lp.	Przebieg	Wartość skuteczna	Składowa stała	Współczynnik kh
								Pomierzony	Obliczony
-	-	V	V	%	%
1	Trójkątny	8,85	0	11	7
2	Prostokątny	9,56	0	36	32

Przykładowe wzory i obliczenia:

• Obliczanie wartości skutecznej napięcia dla przebiegu trójkątnego:

• Obliczanie wartości współczynnika zawartości harmonicznych dla przebiegu trójkątnego:

0,07 * 100% = 7%

• Obliczanie wartości skutecznej napięcia dla przebiegu prostokątnego:

• Obliczanie wartości współczynnika zawartości harmonicznych dla przebiegu prostokątnego:

= 0,32*100% = 32%

WNIOSKI:

- Dla przebiegu prostokątnego mogliśmy zaobserwować więcej harmonicznych niż dla przebiegu trójkątnego.

- Dla przebiegu trójkątnego wartość maksymalna amplitudy jest większa od wartości maksymalnej pierwszej harmonicznej, zaś dla przebiegu prostokątnego wartość maksymalna jest mniejsza od wartości maksymalnej pierwszej harmonicznej. Zależy to od współczynnika zawartości harmonicznych, który dla przebiegu prostokątnego wynosi 36%, zaś dla przebiegu trójkątnego 11%.

- Szereg Fouriera zawiera tylko nieparzyste harmoniczne, ponieważ są to funkcje asymetryczne o odwrotnej zgodności półokresów.

- Szereg Fouriera nie posiada składowej stałej ponieważ wartość średnia badanych funkcji za okres jest równa 0.

- W wynikach pojawiły się niewielkie różnice pomiędzy wartościami obliczonymi ze wzoru, a wartościami odczytanymi z oscyloskopu. Odchylenia te wynikają z niedokładności przyrządów pomiarowych oraz nieprecyzyjnym odczytywaniu wartości z oscyloskopu.

- Przebieg trójkątny i prostokątny różnią się od siebie ilością harmonicznych oraz amplitudą

- Im przebieg jest bardziej zbliżony do sinusoidalnego tym zawartość harmonicznych jest mniejsza, dlatego współczynnik zawartości harmonicznych się różni w zależności od badanego przebiegu

Do przygotowania sprawozdania korzystaliśmy ze skryptu „Laboratorium z podstaw elektrotechniki” Jadwiga Bek, Ewa Hojnacka, Stanisław Hałgas, Marek Korzybski, Sylwia Kozłowska, Andrzej Kuczyński, Hanna Morawska.

---