26-03-2001

• Test dla wskaźnika struktury - test parametryczny

Założenia:

• populacja generalna ma rozkład dwupunktowy z parametrem p - tzn. frakcją elementów wyróżnionych w populacji

• z populacji tej wylosowano niezależne do próby dużą liczbę n elementów (n>100) i w oparciu o wyniki tej próby weryfikujemy H₀, że wskaźnik struktury równa się wartości hipotetycznej

Stawiamy hipotezy:

H₀: p = p₀ H₁: p ≠ p₀

p - (nieznany) wskaźnik struktury populacji generalnej

p₀ - hipotetyczna wartość wskaźnika struktury populacji generalnej

Obliczamy statystykę u:

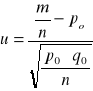
gdzie: m - liczba elementów wyróżnionych

n - liczebność próby

q₀ = 1 - p₀

Wartość statystyki u porównujemy z wartością krytyczną u_α odczytaną dla danego poziomu istotności:

• jeżeli wartość statystyki u znajduje się w obszarze krytycznym - hipotezę zerową odrzucamy,

• jeżeli wartość statystyki u znajduje się poza obszarem krytycznym - nie ma podstaw do odrzucenia hipotezy zerowej.

• Test dla dwóch wskaźników struktury - test parametryczny

Założenia:

• badamy ze względu na cechę niemierzalną dwie populacje generalne o rozkładach dwupunktowych z parametrami p₁ i p₂

• z populacji tej wylosowano niezależne dwie duże próby o liczebnościach n₁ i n₂ elementów (n₁,n₂>100) i w oparciu o wyniki tej próby weryfikujemy H₀, że wskaźniki struktury obu populacji p₁ i p₂ są jednakowe

Stawiamy hipotezy:

H₀: p₁ = p₂ H₁: p₁ ≠ p₂

p₁, p₂ - (nieznane) wskaźniki struktury populacji generalnej

Na podstawie prób obliczamy wartość średniego wskaźnika struktury z obu prób:

Obliczamy wartość pseudoliczebności próby:

Obliczamy statystykę u:

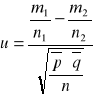
gdzie: m₁, m₂ - liczba elementów wyróżnionych w każdej z prób

n₁, n₂ - liczebności każdej z prób

Wartość statystyki u porównujemy z wartością krytyczną u_α odczytaną dla danego poziomu istotności:

• jeżeli wartość statystyki u znajduje się w obszarze krytycznym - hipotezę zerową odrzucamy,

• jeżeli wartość statystyki u znajduje się poza obszarem krytycznym - nie ma podstaw do odrzucenia hipotezy zerowej.

• Test zgodności χ² (Pearsona) - test nieparametryczny

Test zgodności χ² pozwala na weryfikację hipotezy, że populacji ma określony rozkład, a więc test ten pozwala zweryfikować rozkład empiryczny.

• Stosujemy hipotezę zerową, że populacja generalna ma rozkład normalny.

• Hipoteza alternatywna zaprzecza hipotezie zerowej (rozkład nie jest normalny).

Założenia:

• z populacji generalnej losujemy dużą n elementową próbę

• rozkład populacji generalnej nie jest znany

Z wyników próby tworzymy rozkład empiryczny o r - rozłącznych klasach - otrzymujemy rozkład hipotetyczny

Z rozkładu hipotetycznego obliczamy dla każdej r klasy prawdopodobieństwo p_i. Mnożąc p_i przez liczebność całej próby otrzymujemy liczebności teoretyczne.

Porównujemy liczebności teoretyczne i empiryczne:

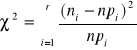
gdzie: n_i - liczebność empiryczna i-tego przedziału klasowego

r - liczba przedziałów klasowych

n_i⋅p_i - liczebność teoretyczna w i-tym przedziale klasowym

Obszar krytyczny w tym teście buduje się prawostronnie - wartość statystyki χ² porównujemy z wartością krytyczną odczytaną z tablicy χ² przy α poziomie istotności i przy r - 1 lub r - k - 1 stopniach swobody:

(k - liczba parametrów szacowanych na podstawie próby, np. (m, σ) szacowane na podstawie (
, S_x) → k=2)

• jeżeli χ² ≥ χ_α² - hipotezę zerową odrzucamy,

• jeżeli χ² < χ_α² - nie ma podstaw do odrzucenia hipotezy zerowej.

ANALIZA STATYSTYCZNA - c.d.

b. ANALIZA WSPÓŁZALEŻNOŚCI - RACHUNEK KORELACJI I REGRESJI

W badaniu współzależności zjawisk rozróżniamy dwa rodzaje zależności:

• zależność funkcyjną - polega na tym, że zmiana wartości jednej zmiennej powoduje ściśle określoną zmianę wartości drugiej zmiennej - oznacza to, że określonej wartości jednej zmiennej odpowiada ściśle określona i tylko jedna wartość drugiej zmiennej

• zależność stochastyczna - to zależność pomiędzy dwoma zmiennymi losowymi polegająca na tym, że ze zmianą jednej z nich zmienia się rozkład prawdopodobieństwa drugiej zmiennej

• z tą zależnością mamy do czynienia wtedy, gdy wpływ jednej zmiennej na drugą zależny jest od czynników przypadkowych wspólnie działających na obie zmienne

• szczególnym przypadkiem tej zależności jest zależność korelacyjna - występuje ona wówczas, gdy określonym wartościom jednej zmiennej przyporządkowuje się pewne średnie z kilku wartości drugi zmiennej

• Metody wyznaczania zależności korelacyjnej

1. Najprostszym sposobem jest zgrupowanie materiału w szeregi statystyczne wg cech, które chcemy badać:

• jeżeli wzrostom wartości danych jednego szeregu statystycznego odpowiadają spadki wartości drugiego szeregu, wówczas mamy do czynienia z korelacją ujemną

• jeżeli wzrostom wartości danych jednego szeregu statystycznego odpowiadają wzrosty wartości danych drugiego szeregu, a spadkom odpowiadają spadki wówczas mamy do czynienia z korelacją dodatnia

2. Diagram korelacyjny - jest to przeniesienie na wykres w fazie punktów danych liczbowych, co w efekcie daje pewien rozrzut

• Diagram korelacyjny umożliwia wstępną ocenę siły i kierunku zależności, a także daje podstawę do wyboru odpowiedniej funkcji matematycznej opisującej zależność między badanymi zmiennymi.

skutek

y y y

. _. .^._. . .^. _. ^.. _.

. _.. ^. . _. . . ^.. _. .. _. ^.. _. . . ^{. .}_. .

. . _. ^. _. .^. . . . _. ^. . _. . . . ^. .. _.^. . ^. .

. . . _. ^. . . ^. . . ^.. _. ^. _. . ^. . _. ^. . ^. .

. . ^. . ^. . ^. . _. . ^. . ^{. .}. ^{. .}

x x x

przyczyna

korelacja dodatnia korelacja ujemna brak zależności

x ↑ to y ↑ x ↑ to y ↓ między badanymi

x ↓ to y ↓ x ↓ to y ↑ cechami

3. Współczynnik korelacji Pearsona

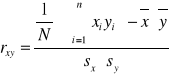
Wskazuje na kierunek powiązania:

• jeżeli r_(x;y) = -1 - doskonała korelacja ujemna,

• jeżeli -1 < r_(x;y) < 0 - niedoskonała korelacja ujemna,

• jeżeli r_(x;y) = 0 - brak związku między badanymi cechami,

• jeżeli 0 < r_(x;y) < 1 - niedoskonała korelacja dodatnia,

• jeżeli r_(x;y) = 1 - doskonała korelacja dodatnia.

Wskazuje na siłę powiązania:

• jeżeli r_(x;y) zbliża się do 0, oznacza to, że nie ma związku między badanymi cechami,

• jeżeli r_(x;y) zbliża się do 1 lub -1, oznacza to, że związek między badanymi cechami jest silny.

x, y - cechy ilościowe (mierzalne)

• Równanie regresji

• jest ilościowym wyrazem zależności między określonymi wartościami zmiennej niezależnej i odpowiadającymi im średnimi wartościami zmiennej zależnej

Mamy dwa równania regresji:

X - zmienna niezależna

Y - zmienna zależna

X - zmienna zależna

Y - zmienna niezależna

a_(x) , a_(y) - wyrazy wolne równania regresji - nie posiadają samodzielnej treści ekonomicznej - nie interpretujemy ich

b_(x) , b_(y) - współczynniki regresji - wartość współczynnika regresji wyraża o ile przeciętnie zmieni się (wzrośnie lub zmaleje) zmienna zależna, jeśli zmienna niezależna wzrośnie o jednostkę

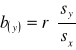
y y y y y

x
x x
x x

r_(x;y) = -1 0 < r_(x;y) < 1 r_(x;y) = 0 -1< r_(x;y) < 0 r_(x;y) = -1

im mniejszy kąt,

tym zależność

jest silniejsza

• Odchylenie standardowe składnika resztowego (średni błąd szacunku)

• szacując wartość y na podstawie wartości x (lub odwrotnie) musimy się liczyć z możliwością popełnienia błędu - jeśli porównamy wartości empiryczne z wielkościami teoretycznymi (obliczonymi na podstawie funkcji regresji), to zauważymy, że pomiędzy nimi występują różnice

Pomiaru tych odchyleń dokonujemy obliczając średni błąd szacunku S.

• względem cechy y:

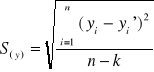
gdzie: y_i - wartości empiryczne

y_i' - wartości teoretyczne (wyzn. na podst. równania regresji)

n - liczebność próby

k - liczba szacowanych parametrów

- gdy znamy r_(x;y)

gdzie: s_y - odchylenie standardowe

• względem cechy x:

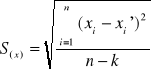
Wielkość odchylenia standardowego składnika resztowego informuje o ile przeciętnie można się pomylić szacując wartości zmiennych x i y na podstawie funkcji regresji.

(Wielkość błędu mierzy dokładnie przewidywanie zmiennej na podstawie funkcji regresji.)

• Miary dobroci dopasowania

• służą do oceny stopnia dopasowania funkcji regresji do danych empirycznych

• współczynnik determinacji - informuje jaki procent zmienności zmiennej objaśnianej jest wyjaśnione przez wyznaczone równanie regresji:

• współczynnik indeterminacji - pomnożony przez 100 określa procent zmienności zmiennej objaśnianej niewyjaśniony daną regresją

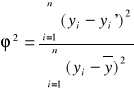
• gdy współczynnik determinacji dąży do jedności, a współczynnik indeterminacji dąży do zera, wówczas statystyczna dobroć dopasowania funkcji rośnie

• gdy współczynnik determinacji dąży do zera, a współczynnik indeterminacji dąży do jedności, wówczas statystyczna dobroć dopasowania funkcji maleje

• w przypadku gdy współczynnik determinacji równa się jedności, a współczynnik indeterminacji równa się zeru mamy sytuację, w której zaobserwowane punkty leżą dokładnie na prostej

• w przypadku gdy współczynnik determinacji równa się zeru, a współczynnik indeterminacji równa się jedności wówczas występuje maksymalne możliwe odchylenie się punktów od dopasowanej prostej

• współczynnik zmienności resztowej - informuje jaki procent zaobserwowanej zmienności zmiennej objaśnianej stanowią odchylenia przypadkowe

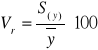
gdzie: S_(y) - odchylenie standardowe składnika resztowego

• Test istotności dla współczynnika korelacji - test parametryczny

W analizie korelacji dokonuje się sprawdzenia dotyczącej otrzymanego z próby współczynnika korelacji. W zależności od przyjętych założeń test istotności dla współczynnika korelacji jest następujący:

Założenia:

• mamy dwuwymiarowy rozkład badanych cech x i y w populacji generalnej, który jest normalny lub zbliżony do normalnego

• z populacji tej wylosowano n elementową próbę i na podstawie tej próby należy zweryfikować hipotezę zerową, że zmienne x i y nie są skorelowane

H₀: ρ = 0 H₁: ρ ≠ 0 ∨ H₁: ρ < 0 ∨ H₁: ρ > 0

ρ - współczynnik korelacji w populacji generalnej

Obliczamy statystykę:

• dla n ≥ 122 - statystyka u:

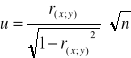
• dla n < 122 - statystyka t:

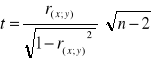
Obliczone wartości statystyk porównujemy z odpowiednimi wartościami krytycznymi: u_α (odczytaną z tablicy rozkładu normalnego) lub t_α (odczytaną z tablicy t-studenta przy poziomie istotności α i n-2 stopniach swobody).

Jeżeli wartość danej statystyki leży w obszarze krytycznym - odrzucamy hipotezę zerową (o braku związku między cechami) na korzyść hipotezy alternatywnej. Jeżeli wartość statystyki leży poza obszarem krytycznym - nie ma podstaw do odrzucenia hipotezy zerowej.

• Test istotności dla współczynnika regresji liniowej - test parametryczny

Bardzo często zdarza się, że w analizie regresji dokonuje się sprawdzenia hipotezy dotyczącej istotności otrzymanego z próby współczynnika regresji liniowej.

• Jeśli współczynnik ten okaże się istotnie różny od zera, to dopiero wówczas można używać otrzymanej funkcji regresji jako narzędzia przy dokonywaniu prognozy wartości badanej cechy na podstawie wartości drugiej skorelowanej z nią cechy.

• Jeżeli natomiast współczynnik regresji otrzymany z próby nie okaże się istotnie różny od zera, to wskazuje to na brak zależności między badanymi zmiennymi.

Założenia:

• mamy dwuwymiarowy rozkład badanych cech x i y w populacji generalnej, który jest normalny lub zbliżony do normalnego

• z populacji tej wylosowano n elementową próbę i na podstawie wyników tej próby należy zweryfikować hipotezę zerową, że współczynnik regresji β liniowej funkcji regresji w populacji generalnej ma określoną wartość

H₀: β = β₀ H₁: β ≠ 0

β - współczynnik regresji populacji generalnej

β₀ - wartość hipotetyczna

Na podstawie wyników n elementowej próby szacujemy równanie regresji:

y_(x)' = a_(y) + b_(y)⋅ x (b_(y) - współczynnik regresji obliczony na podstawie próby)

Obliczamy odchylenie standardowe składnika resztowego:

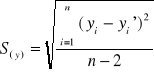
gdzie: y_i - wartości empiryczne zmiennej y

y_i' - wartości teoretyczne zmiennej y (wyzn. na podst. równania regresji)

n - liczebność próby

Obliczamy statystykę t:

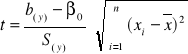
gdzie: S_(y) - odchylenie standardowe składnika resztowego

Wartość statystyki t porównujemy z wartością krytyczną t_α:

• jeżeli |t| ≥ t_α - H₀ odrzucamy,

• jeżeli |t| < t_α - nie ma podstaw do odrzucenia H₀ .

• Test serii - test nieparametryczny

Należy do najważniejszych nieparametrycznych testów istotności.

Serią nazywamy każdy podciąg złożony z kolejnych elementów jednego rodzaju utworzony w ciągu uporządkowanych w dowolny sposób elementów drugiego rodzaju.

Test serii jest zazwyczaj stosowany do sprawdzania hipotezy o liniowej postaci funkcji regresji.

Założenia:

• daną populację badamy ze względu na dwie cechy x i y

• z populacji tej wylosowano n elementową próbę i na podstawie wyników tej próby należy zweryfikować hipotezę zerową, że funkcja regresji y_(x) w populacji generalnej jest liniowa

Stawiamy hipotezy:

H₀: y_(x)' = α + β ⋅ x H₁: y_(x)' ≠ α + β ⋅ x

Z wyników próby wyznaczamy funkcję regresji:

y_(x)' = a_(y) + b_(y) ⋅ x

Porównujemy wartości empiryczne i teoretyczne:

• jeżeli wartości empiryczne y_i są większe od wartości teoretycznych y' - nadajemy im symbol a

• jeżeli wartości empiryczne y_i są mniejsze od wartości teoretycznych y' - nadajemy im symbol b

• jeżeli wartości empiryczne y_i są równe wartościom teoretycznym y' - nie bierzemy tego przypadku pod uwagę

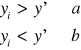
Liczymy serie (k - liczba serii):

• jeżeli k ≥ k_* - odrzucamy H₀

• jeżeli k > k_* - nie ma podstaw do odrzucenia H₀ (o liniowości funkcji regresji)

09-04-2001

• Korelacja wieloraka i cząstkowa

• Korelacja wieloraka - występuje wówczas, porównujemy ze sobą więcej niż dwie cechy.

• Korelacja cząstkowa - polega na tym, że porównujemy ze sobą dwie cechy z równoczesnym założeniem, że istnieją i mają wpływ na dane zjawisko inne cechy, od których świadomie się abstrahuje poprzez ich eliminację.

• Współczynnik korelacji cząstkowej w przypadku trzech zmiennych:

y - zmienna objaśniana

x₁, x₂ - zmienne objaśniające

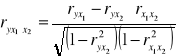
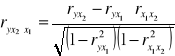
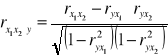
• Współczynnik korelacji wielorakiej w przypadku trzech zmiennych:

• Regresja wieloraka

gdzie: Y' - zmienna objaśniana

X_i - zmienne objaśniające

a₀ - wyraz wolny funkcji regresji

a_i - współczynnik regresji

ξ - składnik losowy

• W przypadku trzech zmiennych:

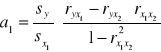
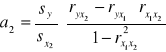
gdzie: s_y ,
- odchylenia standardowe zmiennych y, x₁, x₂

• Odchylenie standardowe składnika resztowego

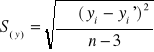
• Współczynniki β - miara relatywnego wpływu zmiennych objaśniających na zmienną objaśnianą

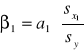
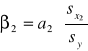
• Korelacja rang - Spearmana

Metoda zwana korelacją rang (lub korelacją kolejności) ma zastosowanie wówczas, gdy badana zbiorowość jest nieliczna, mniejsza niż 30 jednostek.

W przypadku, gdy pomiędzy badanymi zjawiskami lub cechami występuje związek, wówczas ranga (kolejność) rozpatrywana według wielkości skojarzonych wartości zmiennych x i y będzie taka sama lub też bardzo podobna.

• Współczynnik korelacji Spearmana

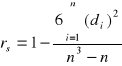
-1 < r_s < 1

gdzie: n - liczebność próby

d_i - różnica pomiędzy rangą cechy x i y (
)

• Test istotności dla współczynnika korelacji rang

H₀: ρ_s = 0 H₁: ρ_s ≠ 0 ∨ H₁: ρ_s < 0 ∨ H₁: ρ_s > 0

• dla n < 10 - statystyka t:

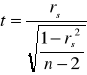
gdzie: ρ_s - współczynnik korelacji rang populacji generalnej

r_s - współczynnik korelacji rang obliczony z próby

n - liczebność próby

• dla n ≥ 10 - rozkład współczynnika korelacji rang jest normalny - test weryfikujący H₀ jest oparty o statystykę u o rozkładzie normalnym:

Wartość obliczonej statystyki porównujemy z odpowiednimi wartościami krytycznymi: t_α (odczytaną z tablicy t-studenta przy poziomie istotności α i n - 2 stopniach swobody) lub u_α (odczytaną z tablicy rozkładu normalnego).

Jeżeli wartość danej statystyki leży w obszarze krytycznym - odrzucamy hipotezę zerową na korzyść hipotezy alternatywnej. Jeżeli wartość statystyki leży poza obszarem krytycznym - nie ma podstaw do odrzucenia hipotezy zerowej.

Przykład 1

Produkcja budowlano-montażowa oraz przeciętne zatrudnienie w Polsce w latach 1987-1996 przedstawia się następująco:

Lata	Produkcja (x) [mld zł]	Zatrudnienie (y) [tys. osób]	Rangi		d = Rx - Ry	d^2
								Rx	Ry
1987	50	646	1	2	-1	1
1988	53	645	2	1	1	1
1989	61	716	3	7	-4	16
1990	66	692	4	3	1	1
1991	71	693	5	4	1	1
1992	78	714	6	6	0	0
1993	79	738	7	9	-2	4
1994	86	704	8	5	3	9
1995	92	732	9	8	1	1
1996	99	756	10	10	0	0

Σ = 34

Wyznaczanie współczynnika korelacji rang:

• uporządkowanie wyjściowych danych wg rosnących wariantów jednej z cech (tu: wg produkcji)

• uporządkowanym wartościom zmiennych nadajemy następne numery kolejnych liczb naturalnych - czynność tę nazywamy rangowaniem (sposób rangowania musi być jednakowy dla obu zmiennych)

• w przypadku gdy występują jednakowe wartości zmiennych przyporządkowujemy im średnią arytmetyczną obliczoną z ich kolejnych numerów

• wyznaczamy wartości d i d²

• obliczamy wartość współczynnika korelacji rang:

Odp. Pomiędzy produkcją budowlano-montażową a zatrudnieniem istnieje silna dodatnia zależność korelacyjna. Wraz ze wzrostem produkcji wzrasta zatrudnienie.

Przykład 2

Spożycie mięsa na jedną osobę oraz dochód w przeliczeniu na osobę w gospodarstwie domowym w próbie dziewięciu gospodarstw pracowniczych w Poznaniu w 1994r. przedstawia tabela:

Dochód (x) [mln zł/os]	Spożycie mięsa (y) [kg/os]	Uporządkowanie (rosnące)		Rangi		d	d^2
				x	y			Rx	Ry
9	20	9	20	1	1	0	0
11	24	11	24	2	2	0	0
12	25	12	25	3	3	0	0
15	27	15	27	4	5	-1	1
17	29	17	29	5	7,5	-2,5	6,25
18	29	18	29	6	7,5	-1,5	2,25
28	32	18	26	7	4	3	9
22	28	22	28	8	6	2	4
18	26	28	32	9	9	0	0

Σ = 22,5

1. Czy prawdziwe jest przypuszczenie, że pomiędzy wyróżnionymi zmiennymi występuje związek korelacyjny?

2. Sprawdzić istotność obliczonego współczynnika korelacji rang na poziomie istotności α = 0,05.

ad. a)

Odp. Między badanymi cechami zachodzi silna dodatnia zależność korelacyjna. Wraz ze wzrostem dochodów wzrasta spożycie mięsa.

ad. b)

H₀: ρ_s = 0 H₁: ρ_s ≠ 0

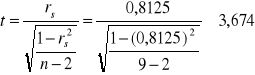
wartość krytyczna odczytana z tablic:

|t| > t_α

- ∞ -2,365 2,365 3,674 ∞

Odp. Odrzucamy hipotezę zerową, co oznacza istotną statystycznie korelacją między badanymi cechami.

• Korelacja cech jakościowych

W badaniach statystycznych zachodzi często potrzeba ustalenia kontyngencji między badanymi cechami x i y, z których obie (lub przynajmniej jedna z nich) mają charakter jakościowy.

W takim przypadku buduje się tablice wielodzielne o określonej liczbie kolumn i wierszy.

Najprostsza tablica wielodzielna jest tablicą kontyngencji 2 × 2, tj. o 2 wierszach i 2 kolumnach:

y x	+	−	razem
+	a	b	a + b
−	c	d	c + d
razem	a + c	b + d	n

a - liczba jednostek posiadających cechę x i y

b - liczba jednostek posiadających cechę x i nie posiadających cechy y

c - liczba jednostek posiadających cechę y i nie posiadających cechy x

d - liczba jednostek nie posiadających cechę x i y

• Współczynnik kontyngencji Pearsona

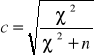
Kres górny współczynnika zależy od liczby kolumn i wierszy w tablicy wielodzielnej. Im więcej kolumn i wierszy, wartość współczynnika jest większa. Dlatego też otrzymaną z obliczeń wartość współczynnika kontyngencji należy rozpatrywać w stosunku do wartości maksymalnej dla danej tablicy wielodzielnej:

• w przypadku tablicy kwadratowej:

gdzie: k - liczba kolumn

• dla tablic prostokątnych:

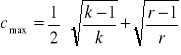
gdzie: k - liczba kolumn

r - liczba wierszy

Wartość skorygowana współczynnika kontyngencji:

Przykład 3

W pewnym przedsiębiorstwie przeprowadzono badanie wśród 200 pracowników mające na celu uzyskanie odpowiedzi na pytanie, czy płeć wywiera wpływ na palenie papierosów? Otrzymane wyniki przedstawia tabela:

płeć palenie pap.	M	K	Razem
TAK	70	30	100
NIE	50	50	100
Razem	120	80	200

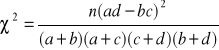
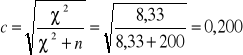
Odp. Pomiędzy cechami zachodzi słaby związek korelacyjny.

Przykład 4

W pewnym zakładzie pracy postanowiono sprawdzić czy absencja w pracy zależy od płci pracowników. Zebrano dane:

płeć absencja [dni]	M	K	Razem
0 - 5	300	500	800
5 - 20	80	70	150
20 i więcej	20	30	50
Razem	400	600	1000

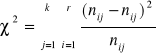
• Obliczamy liczebności teoretyczne
  (mnożąc sumę liczebności i-tego wiersza przez sumę liczebności j-tej kolumny i dzieląc przez ogólną liczebność):

Liczebności empiryczne n	Liczebności teoretyczne
300	320	-20	400	1,25
80	60	20	400	6,67
20	20	0	0	0,00
500	480	20	400	0,85
70	90	-20	400	4,44
30	30	0	0	0,00
				Σ^2 = 13,19

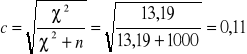
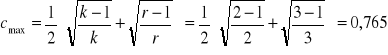
Odp. Pomiędzy cechami istnieje mały stopień skojarzenia.

23-04-2001

c. ANALIZA DYNAMIKI

Analiza dynamiki dotyczy szeregów czasów:

• szereg czasowy - to ciąg wartości badanego zjawiska obserwowanego w kolejnych jednostkach czasu

• szereg czasowy momentów - gdy zmienność cechy jest skokowa

• szereg czasowy okresów - gdy zmienność cechy jest ciągła

W analizie statystycznej posługujemy się liczbami absolutnymi i względnymi:

• wielkości absolutne - powstają przez zliczenie, mierzenie, ważenie i wycenę jednostki; wyrażają one rozmiar badanego zjawiska; każda liczba absolutna jest liczbą mianowaną

• wielkości względne - powstają przez porównanie dwóch liczb ze sobą; wyrażają one zatem rozmiary jednego zjawiska w porównaniu z rozmiarami drugiego zjawiska

Dopiero zestawienie liczb absolutnych i liczb względnych daje pełen obraz badanego zjawiska.

Do liczb względnych zaliczamy wskaźniki, wśród których wyróżnić można:

• wskaźniki struktury - określają jaką część całości przedstawiają wyróżnione elementy

• wskaźniki natężenia - powstają przez porównanie dwóch różnych (ale pozostających do siebie w logicznym związku) wielkości ze sobą, np. gdy porównujemy liczbę ludności z powierzchnią - powstaje gęstość zaludnienia

• wskaźniki dynamiki - powstają przez porównanie dwóch wielkości z różnych okresów; należą do nich mierniki dynamiki i indeksy dynamiki

Wskaźniki dynamiki

a. Mierniki dynamiki

• Przyrost absolutny - najprostszy miernik dynamiki - jest to różnica pomiędzy poziomem zjawiska w okresie badanym a poziomem zjawiska w okresie przyjętym za podstawę porównania:

• przyrost absolutny jednopodstawowy - ma jedną stałą podstawę porównania

• przyrost absolutny łańcuchowy - podstawa badania zmienia się z okresu na okres

gdzie: Y_n - poziom zjawiska w okresie badanym

Y₀ - poziom zjawiska w okresie podstawowym (bazowym)

Y_n-1 - poziom zjawiska w okresie poprzedzającym okres badany

• przyrosty te informują, o ile wzrósł lub zmalał poziom badanego zjawiska w porównaniu z okresem przyjętym za podstawę badania

• przyrosty absolutne są wielkościami mianowanymi wyrażanymi w tych samych jednostkach, co badane zjawisko

• nadają się do porównywania ze zmianami innych zjawisk, które są wyrażone w innych jednostkach miary

• zazwyczaj za podstawę badania wybiera się rok, który stanowił jakiś przełom, przeobrażenie w badanym zjawisku (np. w Polsce - 1990r.); nie wybiera się skrajnych wartości zjawiska

• Przyrost względny - jest to stosunek przyrostu absolutnego zjawiska do jego poziomu w okresie przyjętym za podstawę porównania

• przyrost względny jednopodstawowy:

• przyrost względny łańcuchowy:

• jeśli przyrost względny pomnożymy przez 100, to otrzymamy tempo przyrostu

• Przyrosty mogą być wielkościami dodatnimi, ujemnymi lub równymi zero:

• jeśli przyrost jest dodatni oznacza to, że wystąpił wzrost badanego zjawiska w okresie badanym w stosunku do okresu porównawczego,

• jeśli przyrost jest ujemny - nastąpiło zmniejszenie się zjawiska,

• jeśli przyrost jest równy zero - nie nastąpiły zmiany w poziomie zjawiska.

b. Indeksy dynamiki

INDEKSY

INDYWIDUALNE AGREGATOWE

jednopodstawowe łańcuchowe wielkości wielkości

absolutnych stosunkowych

wartości ilości cen wydajności wykonania

pracy normy

L P L P

L - Laspeyres'a

P - Paasche'go jednopodstawowe jednopodstawowe

łańcuchowe łańcuchowe

INDEKS INDYWIDUALNY - jest to stosunek wielkości zjawiska w okresie badanym do wielkości tegoż zjawiska w okresie przyjętym za podstawę badania.

Indeksy indywidualne są narzędziem wykorzystywanym przy analizie zjawisk jednorodnych.

• Indeks indywidualny jednopodstawowy:

• Indeks indywidualny łańcuchowy:

• Indeks jest wielkością niemianowaną i może być wyrażony w ułamku lub w procentach:

• jeżeli indeks przyjmuje wartości z przedziału (0;1) lub (0%;100%) świadczy to o spadku wielkości zjawiska w okresie badanym w stosunku do okresu porównawczego

• jeżeli indeks przyjmuje wartości powyżej 1 lub 100% świadczy to o wzroście wielkości zjawiska w okresie badanym w stosunku do okresu porównawczego

• jeżeli indeks = 1 lub = 100% oznacza to, że poziomy zjawiska w okresie badanym i w okresie porównawczym są takie same

• zależności: przyrost względny - indeks indywidualny:

• Średnioroczne tempo zmian - wzrost w dłuższych okresach czasu może być charakteryzowany za pomocą jednej liczby - średniorocznego tempa wzrostu;

W zależności od posiadanych informacji można je obliczyć:

• opierając się na ekstremalnych wielkościach absolutnych (pierwszy i ostatni z badanych okresów):

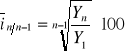
• na podstawie indeksów łańcuchowych:

• na podstawie ekstremalnych indeksów o podstawie stałej przy założeniu, że pierwszy badany okres = 1 lub = 100:

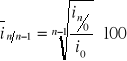
• na podstawie tablic średniego tempa wzrostu

• Średnioroczne tempo zmian w czasie:

lub

Przykład 1

Uczniowie LO w Polsce w latach 1990-1999:

ozn. ind. indywid. jednpodst. ozn. ind. indywid. łańcuchowych

Lata	Uczniowie [tys.]	Przyrost absolutny		Przyrost względny		Indeksy
				jednopod.	łańc.	jednopod.	łańc.		1990 = 100	rok poprzedni = 100
1990	359	0	⋅	0	⋅	100,0	⋅	⋅
1991	363	4	4	0,011	0,011	101,1	101,1	2,0048
1992	371	12	8	0,033	0,022	103,3	102,2	2,0095
1993	373	14	2	0,040	0,005	104,0	100,5	2,0022
1994	375	16	2	0,045	0,005	104,5	100,5	2,0022
1995	383	24	8	0,067	0,021	106,7	102,1	2,0090
1996	400	41	17	0,114	0,044	111,4	104,4	2,0187
1997	422	63	22	0,175	0,055	117,5	105,5	2,0233
1998	444	85	22	0,237	0,052	123,7	105,2	2,0220
1999	463	104	19	0,290	0,043	129,0	104,3	2,0183

Σ = 18,1097

• P_{ab (jednopod.)} - w roku 1999 w stosunku do roku 1990 liczba uczniów LO w Polsce przyrosła o 104 tys.

• P_{ab (łańc.)} - w roku 1999 w porównaniu z rokiem 1998 liczba uczniów LO w Polsce przyrosła o 19 tys.

• przyrosty absolutne są wielkościami dodatnimi - w każdym następnym roku liczba uczniów przyrastała

• i_{n/o (jednopod.)} - w roku 1999 w stosunku do roku 1990 liczba uczniów LO w Polsce wzrosła o 29%.

• indeksy są dodatnie - od roku 1990 można zaobserwować nieprzerwany wzrost liczby uczniów LO

• i_{n/n-1 (łańc.)} - w roku 1999 w porównaniu z rokiem 1998 liczba uczniów LO w Polsce wzrosła o 4,3%.

• z roku na rok tempo zmian było dodatnie - w granicach od 0,5% do 5,5%

• ponieważ wszystkie tempa mają jednakowy znak, można obliczyć średnioroczne tempo zmian (średnioroczne tempo zmian liczymy tylko, gdy dane zjawisko wykazuje jednokierunkowe zmiany + lub - ):

I sposób: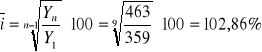

II sposób:

III sposób:

korzystając z funkcji odwrotnej:

• średnioroczne tempo zmian informuje, że liczba uczniów LO w Polsce w latach 1990-1999 wzrastała przeciętnie z roku na rok o 2,86%.

• Zmiana podstaw indeksów

• zamiana indeksów indywidualnych jednopodstawowych na indeksy jednopodstawowe o innej podstawie porównania:

zamiany tej dokonujemy dzieląc każdy indeks jednopodstawowy przez indeks jednopodstawowy z tego okresu, który ma stanowić nową podstawę porównania i mnożąc przez 100

Lata	Indeks: 1990 = 100	Działania	Indeks: 1995 = 100
1990	100,0	(100,0⋅117,9)÷100	84,8
1991	103,4	(103,4⋅117,9)÷100	87,7
1992	107,4	(107,4⋅117,9)÷100	91,1
1993	111,2	(111,2⋅117,9)÷100	94,3
1994	112,9	(112,9⋅117,9)÷100	95,8
1995	117,9	(117,9⋅117,9)÷100	100,0
1996	122,1	(122,1⋅117,9)÷100	103,6
1997	127,1	(127,1⋅117,9)÷100	107,8
1998	131,5	(131,5⋅117,9)÷100	111,5
1999	135,7	(135,7⋅117,9)÷100	115,1

• zamiana indeksów indywidualnych jednopodstawowych na indeksy łańcuchowe:

zamiany tej dokonujemy dzieląc każdy indeks jednopodstawowy przez bezpośrednio poprzedzający go i mnożąc przez 100

Lata	Indeks: 1990 = 100	Działania	Indeks: rok poprzedni = 100
1990	100,0	⋅	⋅
1991	103,4	(103,4÷100,0)⋅100	103,4
1992	107,4	(107,4÷103,4)⋅100	103,9
1993	111,2	(111,2÷107,4)⋅100	103,5
1994	112,9	(112,9÷111,2)⋅100	101,5
1995	117,9	(117,9÷112,9)⋅100	104,4
1996	122,1	(122,1÷117,9)⋅100	103,6
1997	127,1	(127,1÷122,1)⋅100	104,1
1998	131,5	(131,5÷127,1)⋅100	103,5
1999	135,7	(135,7÷131,5)⋅100	103,2

69

---