1. ![]()
;
PRZYKŁADOWE ZADANIA EGZAMINACYJNE
MECHANIKA
Oblicz:
1. ![]()
;
2. ![]()
;
3. ![]()
;
4. ![]()
;
5. ![]()
;
6. ![]()
;
7. ![]()
.
Przedstaw w postaci trygonometrycznej:
![]()
;
![]()
;
![]()
;
![]()
.
Korzystając z postaci trygonometrycznej oblicz:
1. ![]()
;
2. ![]()
;
3. ![]()
;
4. ![]()
;
5. 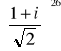
;
6. 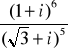
.
Oblicz:
1. ![]()
;
2. ![]()
;
4. ![]()
;
5. ![]()
.
W III. ORAZ IV. WYNIK PRZEDSTAW W POSTACI ALGEBRAICZNEJ !!!
Rozwiąż równania:
![]()
.
![]()
;
![]()
;
![]()
;
![]()
;
![]()
.
Oblicz:
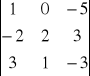
;

;
![]()
oraz ![]()
gdy: 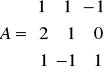
, 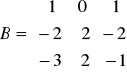
;
![]()
oraz ![]()
gdy: 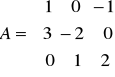
, 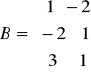
;
![]()
oraz ![]()
gdy ![]()
oraz 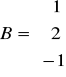
;
![]()
, gdy: 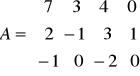
,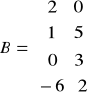
, 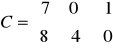
;
![]()
, gdy 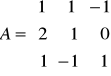
.
Rozwiąż układ równań:
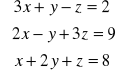
;
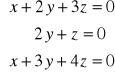
;
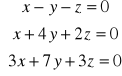
;
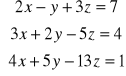
;
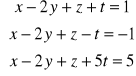
;
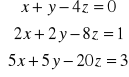
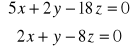
;
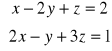
;
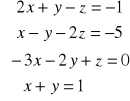
.
Rozwiąż równania macierzowe:
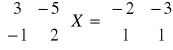
;
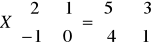
;
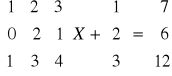
;
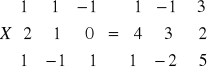
.
Oblicz pole trójkąta o wierzchołkach ![]()
, ![]()
, ![]()
.
Oblicz objętość równoległościanu rozpiętego na wektorach ![]()
, ![]()
, ![]()
.
Znaleźć wektor jednostkowy prostopadły do wektorów ![]()
i ![]()
jednocześnie.
Czy wektory ![]()
i ![]()
są:
prostopadłe?
równoległe?
Napisz równanie płaszczyzny przechodzącej przez punkty ![]()
, ![]()
, ![]()
.
Napisz równanie płaszczyzny przechodzącej przez punkty ![]()
, ![]()
i prostopadłej do płaszczyzny ![]()
.
Napisz równanie płaszczyzny przechodzącej przez punkt ![]()
i prostopadłej do prostej ![]()
.
W jakich punktach płaszczyzna ![]()
przecina osie układu współrzędnych?
Napisz w postaci kierunkowej i parametrycznej równania prostej danej w postaci krawędziowej: 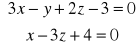
.
Napisz w postaci kierunkowej i parametrycznej równania prostej prostopadłej do płaszczyzny ![]()
i przechodzącej przez punkt ![]()
.
Znajdź współrzędne punktów przecięcia prostej ![]()
z płaszczyznami układu współrzędnych.
Znajdź punkt symetryczny do punktu ![]()
względem płaszczyzny ![]()
.
Znajdź punkt symetryczny do punktu ![]()
względem prostej ![]()
.
Dla jakiej wartości parametru ![]()
prosta ![]()
jest równoległa do płaszczyzny ![]()
?
Dla jakiej wartości parametru ![]()
płaszczyzny ![]()
oraz ![]()
są prostopadłe?
Czy punkty ![]()
, ![]()
, ![]()
![]()
leżą w jednej płaszczyźnie?
Zbadaj monotoniczność ciągu:
1. ![]()
,
2. ![]()
,
3. 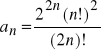
,
4. ![]()
.
Oblicz:
![]()
,
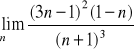
,
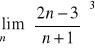
,
![]()
,
![]()
;
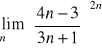
,
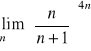
,
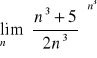
,
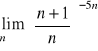
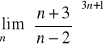
.
Oblicz pochodną funkcji:
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
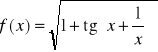
,
![]()
,
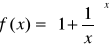
,
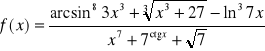
Oblicz ekstrema i zbadaj monotoniczność funkcji:
![]()
.
![]()
.
![]()
,
![]()
,
![]()
,
![]()
,
![]()
.
Znajdź punkty przegięcia wykresu funkcji:
1. ![]()
,
2. ![]()
,
3. ![]()
,
4. ![]()
.
Oblicz:
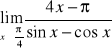
,
![]()
,
![]()
,
![]()
,
![]()
,
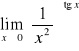
,
![]()
,
![]()
.
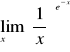
,
![]()
,
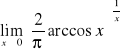
.
Wyznacz wszystkie asymptoty funkcji:
![]()
,
![]()
,
![]()
.
Oblicz całki:
![]()
,
![]()
,
![]()
,
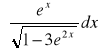
,
![]()
,
![]()
,
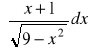
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
,
![]()
![]()
,
![]()
,
![]()
,
![]()
![]()
,
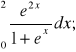
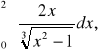
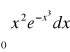
,
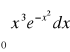
,
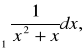
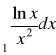
.
Oblicz pole obszaru ograniczonego liniami:
![]()
;
![]()
;
![]()
;
![]()
;
![]()
;
![]()
;
![]()
.
Oblicz długość łuku krzywej
![]()
dla ![]()
;
![]()
![]()
.
Oblicz objętość bryły powstałej przez obrót dookoła osi ox:
krzywej:
![]()
![]()
.
figury płaskiej ograniczonej liniami:
![]()
;
![]()
;
![]()
.
Oblicz pole powierzchni bryły powstałej przez obrót dookoła osi ox krzywej:
![]()
;
![]()
dla ![]()
;
![]()
dla ![]()
;
![]()
.
XIV. Oblicz pochodne cząstkowe I i II rzędu funkcji:
![]()
![]()
![]()
,
![]()
![]()
![]()
![]()
,
![]()
.
Dla danej funkcji ![]()
obliczyć zadane pochodne cząstkowe:
![]()
![]()
;
![]()
, 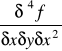
;
![]()
, 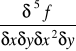
.
XVI. Oblicz ekstrema funkcji dwóch zmiennych:
![]()
![]()
;
![]()
;
![]()
;
![]()
.
1
5
7
9