wagi i po wysuszeniu ustalamy jego ciężar gs. Różnica g_m i g_s daje wagę, czyli objętość wody wyparowanej. Przyjmując, że pory były całkowicie wypełnione wodą, znajdujemy porowatość objętościową V = (gm-gs): przy czym V = objętość ciała próbnego. Z natury rzeczy metoda ta nie jest ścisła, bo nie ujawnia porów kulistych.

b) Doświadczalna na podstawie gęstości. Najpierw ustalamy ciężar gatunkowy całkowicie wysuszonego ciała zaczynowego przez ustalenie jego pojemności V i wagi G wynosi on γ=G/V; następnie rozdrabniamy zaczyn na mączkę i ustalamy jego absolutny ciężar gatunkowy γa. Porowatość wynosi wtenczas w % objętości Vo=(1-γ/ γ_a)*100.

g) Pełna hydratacja i optymalna ilość wody.

Na podstawie wspomnianego wyżej (§ e ) twierdzenia Andregg'a i Hubell'a, że związki uwodnionego cementu maja jednakowy ciężar gatunkowy ciężar gatunkowy γg=2,13 (ściślej ok. 2,2), możemy w przybliżeniu obliczyć tę ilość wody, której potrzebuje cement do pełnej hydratacji; mianowicie powinno być :

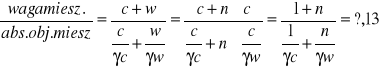
dla c = 3,23 i γ _w =1 wynika stąd n=0,3 ;czyli cement dla pełnej hydratacji potrzebuje wody w ilości ok. 30% swej wagi.

Wartość 30% jest o tyle niedokładna, że wyliczona została przy γ _c =3,23 i γ _g =2,13. z innym otrzymałoby się inne . Poza tym założyliśmy, że objętość zaczynu skamieniałego równa się objętości zaczynu świeżego, co jest nieścisłe. Z dokładniejszą bowiem hydratacją rośnie objętość stwardniałego zaczynu, obserwujemy to jako narastanie w wodzie. 1) wartość 30% jest zatem tylko orientacyjnie słuszna i podlega wahaniom. W każdym razie jednak badacze stwierdzili w zaczynach obecność wody związanej już w ilości 30% jak np. W. Paszkowski w tabl. 48. Ale właśnie w przykładzie Paszkowskiego pełna hydratacja została osiągnięta nie przez sama ilość wody zarobowej ale poprzez przechowywanie ciała próbnego w wodzie czyli przez dalsze doprowadzenie wody podczas tężenia.

Gdybyśmy dodali do cementu tylko 30% wody, a poza tym od zewnątrz niedoprowadzalibyśmy jej więcej podczas tężenia, ilość chemicznie związanej wody byłaby znacznie niższa , bo część wody by wyparowała. Istotnie znaleźli dla cementu typu portl. Wg: H. Wąsowicz przy w./c=0,25....... 13,5% wody związ.

w./c>0,38....... 16,4%

Goslich i Otzen dla norm. Zaczynów 10,3→16,5% wody związ.

Candlot „ 11,5→ 15,5% `' `'

Lea i Desch [40] dla betonu 1:2:4 14→16% '' ''

Z powiększeniem dodatku wody rośnie też ilość wody związanej. Normalnie przyjmuje się że w betonach o wyższym w/c ilość związanej wody wynosi po 28 dniach tężenia na powietrzu ok. 16-28% wagi cementu.

Wg. Lerch'a i Bogue'go ²) można wagę ostatecznie związanej wody dla normalnych warunków obliczyć ze wzoru

Ho= (CaO-1,87* SiO₂)*0,32+1,87*SiO₂*0,16+0,36*Fe₂O₃+0,53*Al₂O₃+0,45*MgO, przy czym

Ho= odsetek wody w stosunku do wagi cementu

CaO itd.= odsetek wagowy danego składnika w cemencie.

Ilość wody obliczona powyższym wzorem wynosiłaby np. dla cementu Kuhl'a wg przykładu § IV 6 a

Ho= (65,3-1,87*18)*0,32+1,87*18*0,16+0,36*5,3+0,53*7,1+0,45*1,5=21,9%

Dla cementu glinowego wg przykładu § IV 6 d ilość wody wynosiłaby:

Ho= (39,1-1,87*5,8)*0,32+1,87*5,8*0,16+0,36*7,1+0,53*45+0,45*0=37,4%

Interesujące jest, że zawartość Ho dla cementu glinowego jest wyższa, co zresztą stwierdzono również doświadczalnie (tabl.47). Częściowo należy to przypisać wpływowi szybkiego tężenia, która zmniejsza ilość wyparowanej wody. To szybsze tężenie w części może być przypisane drobniejszemu przemiałowi cementu glinowego, ale głównie polega ono na odmienności reakcji chemicznych. Wartość Ho zależy u cementu glinowego zresztą również od temperatury otoczenia. Przy temperaturze wody i otoczenia +15 stopni jest ona najwyższa i wynosi do ok. 50% przy czym uwodnienie zaczynu jest prawie całkowite i jego ciężar gat. wynosi γ =2,11. Przy temperaturze +45 stopni hydratacja jest niezupełna , cement glin. wiąże wtenczas tylko ok. 27% wody i jego ciężar gatunkowy jest odpowiednio wyższy i wynosi γ=2,64 [40].

Reasumując stwierdzamy, że chcąc osiągnąć za pomocą wody zarobowej możliwie pełną hydratację cementu, musimy jej dać znacznie więcej niż ta ilość, która ostatecznie będzie związana. Naturalnie możemy pełną hydratację osiągnąć również doprowadzając wodę podczas tężenia przez nawilżanie betonu, takie postępowanie jest lepsze. Wzmagając bowiem przez większy dodatek wody zarobowej intensywność hydratacji powiększamy co prawda ilość gelu, ale zmniejszamy jego gęstość czyli wytrzymałość zaczynu.

Optymalną ilością wody jest zatem ta praktyczna ilość wody zarobowej przy której cement wprawdzie nie ulegnie całkowicie hydratyzacji, ale przy której gel będzie najmniej porowaty.

Ta optymalna ilość wody jest dla różnych cementów różna: średnio wynosi dla zaczynów

z cem. typu portl. w/c = 0,2→0,3

z cem. glinowego w/c = 0,2→0,4 (ale i 0,5, zależnie od cementu).

Przy cemencie glinowym ilość wody, potrzebnej do pełnej hydratacji, i ilość wody optymalnej się prawie pokrywają. Ciała próbne z zaprawy normowej z cementem glinowym o konsystencji wilgotnej przy zawartości 8% wody w stosunku do zaprawy (w/c = 0,32) zawierają na ogół za mało wody. Cement glinowy wogóle nie powinien być przerabiany przy zbyt suchej konsystencji, gdyż może nie starczyć wody na dostateczną jego hydratację.

h) Graniczna wytrzymałość zaczynu bezporowatego.

Przy całkowitym uwodnieniu cementu i jednoczesnym całkowitym zawiązaniu wody, co zresztą możliwe jest tylko w warunkach laboratoryjnych, występuje maksymalna wytrzymałość betonu, będąca wykładnikiem maksymalnej ilości i gęstości gelu. Gęstość gelu jest jednak nawet w tym wypadku jeszcze niezupełna. Cement i woda zawierają bowiem pory powietrzne, które przy normalnym wykonywaniu zaczynu nie dają się usunąć i działają tak jakby cement zarobiony był z nadmiarem wody. Tym się tłumaczy, że nawet najlepszy beton nie osiąga wytrzymałości twardych skał. Laboratoryjnie może jednak i to powietrze być usunięte przez wytwarzanie próżni lub skomprymowanie zaczynu, ¹) , wtenczas jego wytrzymałości mogą osiągnąć bardzo duże wartości. Szczególnie efektowne wyniki osiąga się przez kompresję. Takie doświadczenie przeprowadził Francuz l'Hermite ²). Zarobił on mianowicie cement z 8% wody i sprasował go pod ciśnieniem 3000 at. Wytrzymałość wynosiła już po kilku dniach Rs=1600 kg/cm². Ta ilość wody okazała się o tyle optymalną, że już małe przekroczenie obniżało wytrzymałość. Dla kontroli, ile z tej wytrzymałości przypisać należy reakcji chemicznej, a ile działaniu mechanicznemu wykonał ten autor próbne cylindry z bazaltu zmielonego na miałkość cementu i dodawszy 8 % wody ( błonka na ziarnach grb. ~ 0,001mm) sprasował cylindry pod ciśnieniem 500→2000 at . Wytrzymałość cylindrów bazaltowych wyniosła Rs = ~ 450 kg/cm². Wynika stąd, że większa część wytrzymałości cementu była wynikiem reakcji chemicznych .- Przykład prawie bezporowatego zaczynu widzimy poza tym na rys. 59. wg Eigera [9], gdzie osiągnięta została wytrzymałość przeszło 1700 kg/ cm² .

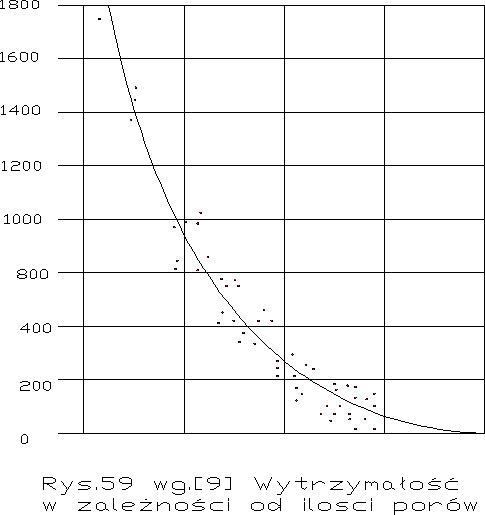
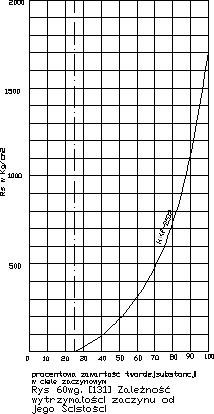
Jeżeli mierzymy próżnie w stwardniałym zaczynie ,- obojętnie jak one powstały , - wtenczas możemy ustalić za A. Eigerem zależności wytrzymałości od porowatości wg. rys.59 lub od zawartości twardej substancji w ciele zaczynowym wg.rys.60. Zależność ta jest mało ścisła i jak stwierdzili Werner i Hedstrom (131) wytrzymałości zaczynów o tej samej zawartości twardej substancji są tym niższe, im wyższe było w/c. Niemniej zależność ta jest wyraźna i może być wyrażona przez krzywą matematyczną. Krzywa rys.60 ma kształt

Rs=0,305. (f-25)²

gdzie f= objętość twardej substancji w %.

Przez ekstrapolację możemy dojść do granicznej i nieprzekraczalnej wytrzymałości zaczynu zawierającego 100% twardej substancji, czyli zaczynu bezporowatego. Wg [9] znaleźli:

Eiger 2200 kg/cm² (por.rys.59)

Hedstrom 1800→1900 kg/cm² (por.rys.60)

Anderegg 2660 kg/cm²

Różnice tłumaczą się po większej części różnicę wymiarów badanych próbek. Jest to w każdym razie wytrzymałość najlepszych skał, a zarazem graniczna wytrzymałość zaczynu, uwarunkowana jedynie wytrzymałością cząsteczkową. Wytrzymałość zwykła jest zatem wg Eigera [7] „wypadkową wytrzymałości molekularnej i czynników, które tę wytrzymałość umniejszają”. Teoretycznie powyższe cyfry nie są jeszcze absolutną górną granicą wytrzymałości. Wg teorii atomowej wytrzymałość ta mogłaby być jeszcze kilkunastokrotnie wyższa, gdyby nie istniały wewnątrz kryształków drobne pęknięcia, pochodzące od naprężeń wewnętrznych na które narażone jest każde większe ciało przy tężeniu. Jaki wpływ ma przekrój ciała na wytrzymałość, widzimy na przykładzie doświadczenia Griffitha [44] z nitkami ze szkła kwarcowego, wyciągniętymi przy temperaturze + 730 stopni ze stopu, który osiągnął uprzednio temperaturę + 1300 stopni.

średnica w mm	1,02	0,107	0,0508	0,0336	0,0178	0,0127	0,0033
wytrzym. na rozrywanie w kg/cm^2	1750	2980	5610	7010	11500	13700	34600

W technologii betonu podobne ciała są oczywiście pozbawione jakiegokolwiek znaczenia. Zawsze jednak wskazuje powyższy przykład dodatkowo na to, że zmniejszenie ilości drobnych rys wewnętrznych np. przez skomprymowanie betonu może dać bardzo dodatnie wyniki. Istotnie wkroczono obecnie już na tę drogę nawet w praktyce.

3.Wytrzymałość na ściskanie.

1. Porowatość, w/c i wytrzymałość zaczynu.

Dopóki ilość wody w zaczynie nie przekracza optymalnej granicy, rośnie wytrzymałość zaczynu z ilością wody na skutek wzrostu ilości gelu i lepszego wypełnienia jam cementu. Gęstość gelu jest przy tym praktycznie prawie niezmienna, bo nie ma nadmiaru wody, więc gel się nie rozrzedza. Dla wzrostu wytrzymałości jest zasadniczo bez różnicy czy ilość gelu wzrasta przez dokładniejszą hydratację, czy też przez większą ilość cementu w jednostce betonu. Zależność między wytrzymałością stwardniałych zaczynów a stopniem hydratacji cementu widzimy według Eigera na rys. 61, przy czym stopień hydratacji został obliczony przez niego wg. wykresu rys.56. Na rys. 61 uderza to, że zasadnicza krzywa nie przechodzi przez punkt zerowy; potrzebny jest pewien minimalny odsetek hydratacji cementu, by w ogóle mogło wystąpić pewne minimum wytrzymałości. Ilość ta wynosi wg Eigera 13% wagi cementu, wg Nedstroma i Werner'a natomiast 25%, różnica polega na tym, że pierwszy badał zaczyny, drudzy natomiast zaprawy wzgl. Betonu. Rys 61 obejmuje wytrzymałości szeregu bardzo różniących się cementów i z bardzo różnych okresów od 1→90 dni, pomimo to zależność wytrzymałości od stopnia hydratacji jest zupełnie wyraźna i wprost proporcjonalna do ilości gelu. Nasuwa się stąd bardzo ważny wniosek, że zarówno wpływ czasu jak i wpływ tzw. jakości cementu na wytrzymałość sprowadzona być może do ilości gelu, które cementy w określonym czasie wytwarzają. Lepsze cementy będą te których wydajność pod względem gelu będzie większa, przy czym obojętne będzie czy ta większa wydajność będzie skutkiem odpowiedniejszego chemicznego składu czy też lepszego przemiału czy też nawet staranniejszego przechowywania na budowie. Jest to odkrycie bardzo ważne, a sformułowanie jego zawdzięczamy A.Eigerowi.

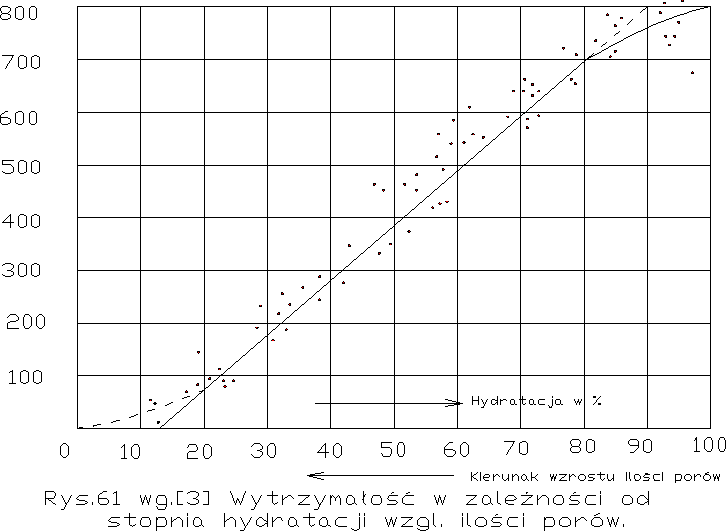
Br. Bukowski doszedł w swej pracy [23] do analogicznego wniosku na całkiem innej drodze. Stwierdził on mianowicie że betony o tej samej wytrzymałości po n dniach mają na ogół równą wytrzymałość również po (n+x) dniach i to niezależnie od ich składu, od jakości cementu i od stosunku w/c ¹) . Da się to wytłumaczyć w ten sposób że równa wytrzymałość betonów po n dniach była wynikiem jednakowej ilości gelu. Ponieważ szybkość wydzielania się gelu u pokrewnych cementów jest niezależna od innych czynników prócz wielkości i ilości ziaren cementowych w betonie, ilość gelu musi być u różnych betonów jednakowa w czasie późniejszym, jeżeli była taka sama w czasie wcześniejszym. Hipoteza Eigera jest zatem w dobrej zgodzie z innymi doświadczeniami.

Zależność między wytrzymałością betonu a ilością cementu przy tym samym stosunku wody do cementu w/c <w/c_opt widzimy na rys. 62. Różnice wytrzymałości pochodzą w tym wypadku również tylko z różnicy ilości gelu w jednostce betonu, gdyż jakość (gęstość) gelu jest u wszystkich betonów jednakowa.

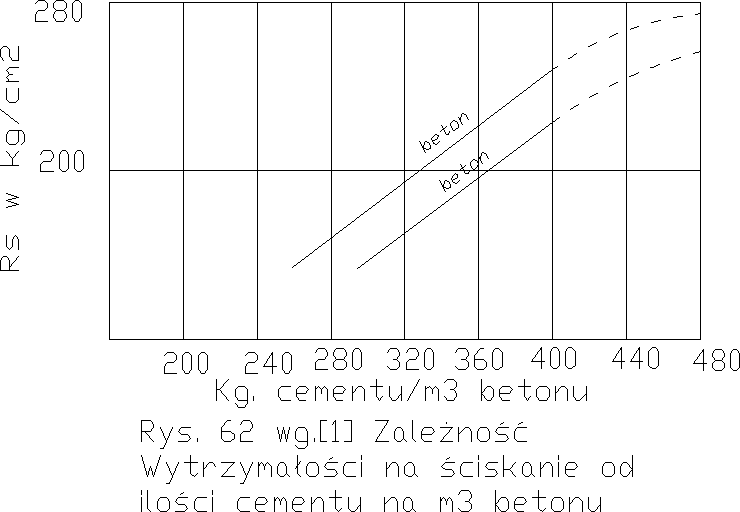
Przykład zależności wytrzymałości betonu od miałkości cementu podaje Herrmann [14] dla zaprawy norm. 1:3, czyli w/c= ~ w/c_opt.

cement	R7	R28(w)	R28(wp)
norm.	220	356	426
odsiany przez sito /4900/	352	510	548

Również w tym wypadku wytrzymałość wzrosła ze zwiększeniem ilości gelu w jednostce betonu na skutek lepszej hydratacji drobniejszych ziaren cementu, zatem mamy to samo zjawisko, tylko na skutek innej przyczyny zewnętrznej.- Wzrost wytrzymałości zaczynu wzgl. betonu ze zwiększeniem ilości gelu występuje jednak tylko dopóty, dopóki jamy kruszywa i próżnie nie zostaną wypełnione gelem. Z chwilą kiedy beton staje się ”nasycony” gelem dalsze wytwarzanie tegoż nie przysporzy mu już wytrzymałości, o czym w rozdz. C.

Wracając do rys.61 można byłoby zamiast wzrastającej hydratacji wykreślić spadającą porowatość. Ze wzrostem porowatości, spowodowanym w tym wypadku przez spadek stopnia hydratacji czyli przez brak gelu, zmniejszy się wytrzymałość. Maksimum wytrzymałości nastąpi wtenczas, kiedy hydratacja będzie zupełna przy jednoczesnym minimum porów.

Jeżeli powiększamy ilość wody dowolnie ponad optimum, hydratacja zawsze będzie pełna, czyli gelu będzie dość, ale będzie porowaty. Zależność wytrzymałości zaczynu od tego stanu widzimy na rys. 63, tylko że w tym wypadku nie jest podany stopień hydratacji, który jest niezmienny i wynosi 100% ¹), lecz porowatość zaczynu wywołana nadmiarem wody.

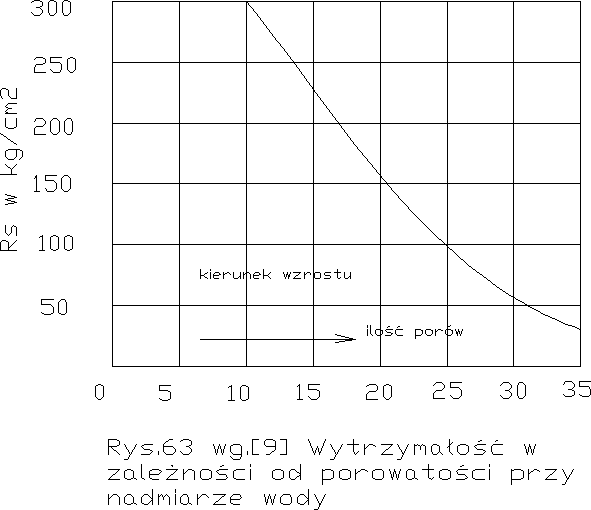
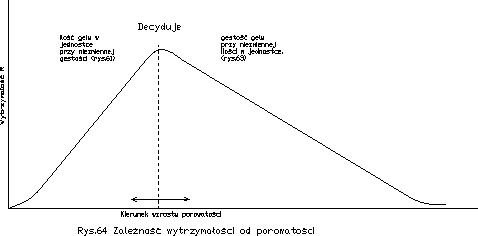
Widzimy więc, że wytrzymałość zaczynu sprowadzić się daje w każdym wypadku do ilości porów w nim : im więcej porów w zaczynie, tym mniejsza jest jego wytrzymałość. Toteż możemy obie krzywe z rys. 61 i 63 połączyć w jedną wspólną krzywą wg. rys. 64, gdzie wytrzymałość R uzależniono od porowatości. Maksimum wytrzymałości jest tam , gdzie porowatość jest minimalna, tj. gdzie teoretycznie cały cement został zhydratyzowany i cała woda zużyta na hydratację. Ponieważ „sprawcą” porowatości jest woda, możemy więc porowatość również zastąpić stosunkiem wody do cementu czyli współczynnikiem wodocementowym w/c lub c/w, który w technologii betonu odgrywa decydującą rolę.

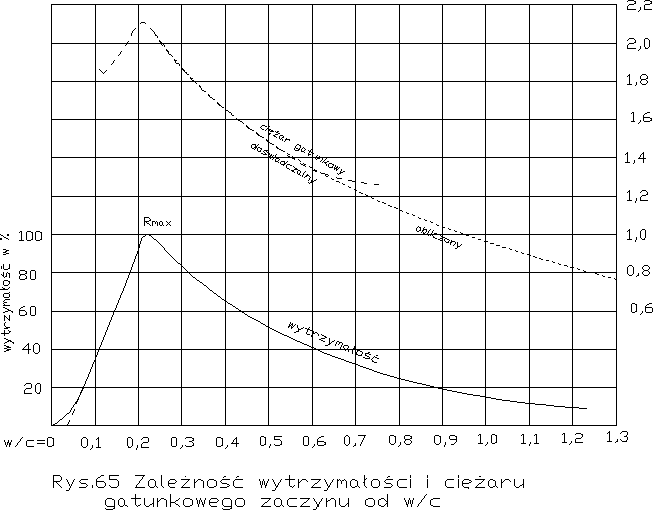
Przebieg krzywej wytrzymałości w zależności od w/c dla zaczynów widzimy na rys. 65, gdzie wytrzymałość wyrażona jest w procentach wytrzymałości R_max przy opt. w/c. Krzywa widoczna na tym rysunku, przedstawia krzywą znalezioną przez różnych badaczy (m.in. Abrams'a, Hummel'a) doświadczalnie jako średnia dla cementów portlandzkich przy zmiennym w/c. Zgodność jej przebiegu z krzywą rys. 64, wzgl. z krzywymi macierzystymi rys. 61 i 63 dowodzi, że porowatość istotnie utożsamiona być może ze stosunkiem w/c. Tę ważną rolę wody w zaczynie ujął W. Paszkowski bardzo trafnie w następującymi słowami [42]: „ilość wody zaczynowej warunkuje i przesądza strukturą zaczynu. Dalsza hydratacja zmniejsza zawartość porów bardzo znacznie, ale zawsze zaczyn bardziej wodnisty zostaje bardziej porowatym.”

b/ Optymalna ilość wody przy dodatku kruszywa

i wpływ rozrzedzenia zaczynu.

Wyżej określiliśmy jako optymalną ilość wody zarobowej tę ilość, która zapewnia najmniejszą porowatość zaczynu, czyli tę ilość, przy której otrzymamy maksymalną wytrzymałość betonu. Tę optymalną ilość wody podaliśmy wyżej orientacyjnie na w/c =0,2→0,4 dla zaczynu z cementu glinowego, a w/c =0,2→0,3 dla pozostałych cementów; u większości cementów w/c_opt mieści się w podanych granicach, ale zdarzają się również znaczne przekroczenia tych granic szczególnie u cementów glinowych.- Dalej podaliśmy na rys. 65 stosunki R/R_max dla różnych w/c. - I te wartości są tylko średnie i zmieniają się od cementu do cementu; zmienność stosunku R/R_max przy tym samym w/c różnych cementów nazywaliśmy wrażliwością na rozrzedzenie zaczynu, przytaczając rys.13 wg Solacolu, gdzie wpływ rozrzedzenia związany jest ze składem chemicznym cementu.

Zarówno wartość w/c_opt. jak i wpływ rozrzedzenia doznają dalszych wahań i zmian, jeżeli od zaczynów przejdziemy do zapraw i betonów. Wtenczas bowiem część wody zostaje wyeliminowana z bezpośredniej akcji uwadniania cementu przez to, że oblepia błonkowo ziarna kruszywa lub nawet wnika w ich pory. Jest ona tym większa, im chudsza jest mieszanka i im większa jest wewnętrzna powierzchnia kruszywa. Woda ta nie tworzy bezpośrednich porów w gelu, ale mimo to powiększa jego ogólną porowatość przez tworzenie kawern na powierzchni styku zaczynu z ziarnami kruszywa. Wpływ porów zaczynowych na wytrzymałość staraliśmy się ująć na rys. 65, wpływ kawern na wytrzymałość będzie podobny, ale nie identyczny. I tu leży największa trudność technologii betonu, zjawiska porowatości są tak złożone że nie mamy jeszcze możliwości zupełnie dokładnego obliczania wytrzymałości betonu na podstawie właściwości materiałów składowych. Dopiero liczne i coraz subtelniejsze badania, uwzględniające z jednej strony podział związków cementu na kryształy i galarety, a z drugiej strony uwzględniając miałkość i strukturę powierzchni kruszywa, pozwolą nam się zbliżyć coraz bardziej do ideału. Ogólna zależność R betonów od w/c jest już dość dobrze, choć tylko z grubsza ujęta, omawiamy ją w rozdz. C. Dokładniejszych badań nad przyczynami odchyleń od tej zależności mamy natomiast dotychczas mało, a nawet zbyt mało.

Niektóre badania w tym kierunku przeprowadzili Probst i Hummel [269], starając się wyjaśnić wpływ gatunku cementu na w/c_opt, i na wrażliwość rozrzedzeniową. W tym celu wykonali oni zaczyny i zaprawy 1:3 o różnym w/c, badając wytrzymałość Rs₂₈ przy przechowaniu komb. wodno-powietrznym. Wyniki porównania cementu glinowego, portl. przedniego i portl.. normalnego mamy na rys.66.

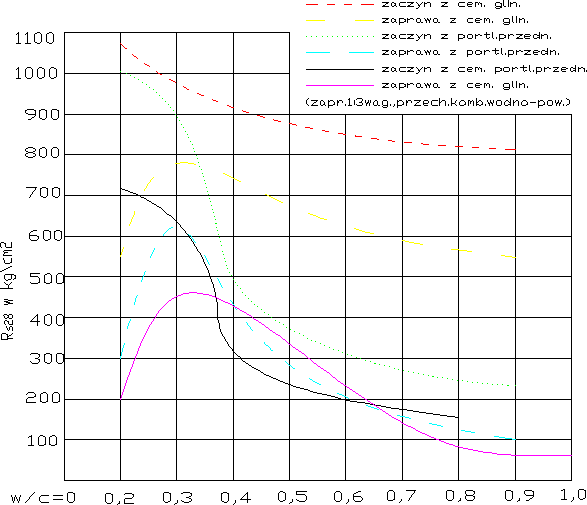
Rys.66 wg [269]. Zależność Rs od w/c zaczynów i zapraw z różnych cementów

Widzimy naprzód, że w w/c_opt. dla zaczynów wynosi 10,2 przesuwając się dla zapraw na 0,3 u wszystkich trzech gatunków cementu. Poza tym jednak zachowują się poszczególne cementy różnie. Cement glinowy jest stosunkowo mało wrażliwy na rozrzedzenie ¹) za to różnica wytrzymałości zaczynu i zaprawy jest w nim dość znaczna i to niezależnie od wielkości w/c. Cementy portlandzkie przedni i normalny , zachowują się dość podobnie, różnica R zaczynu i zaprawy przy w/c=0,3 jest znaczna, przy w/c=0,4 nikła. Od tego punktu różnica u cementu przedniego znowu wzrasta ze wzrostem w/c>0,6, w obydwu wypadkach R zaczynu w porównaniu z R zaprawy jest tym wyższe, iż wyższe jest w/c. Wytłumaczenia tego zjawiska autorzy nie dają. Zapewne stoi ono w związku z faktem , że przy zbyt dużym w/c zaczyn nie jest w stanie więzić wodę ¹) która wycieka i tym samym zmniejsza faktyczny stosunek w/c; gdyby woda nie mogła wyciec, byłyby zapewne R zaczynu i R zaprawy więcej do siebie zbliżone. Charakterystyczne jest to, że cement przedni wykazuje o wiele wyższą wytrzymałość tylko przy niskim w/c (kons. wilg.) i że przy wyższym w/c prawie się nie różni od cementu normalnego. Cement przedni jest wrażliwszy na rozrzedzenie niż normalny. Słusznie wyciągają autorzy stąd wniosek, że obowiązująca dotychczas próba normowa stawia cementy przednie w lepszym świetle, niż odpowiada rzeczywistości. ²)

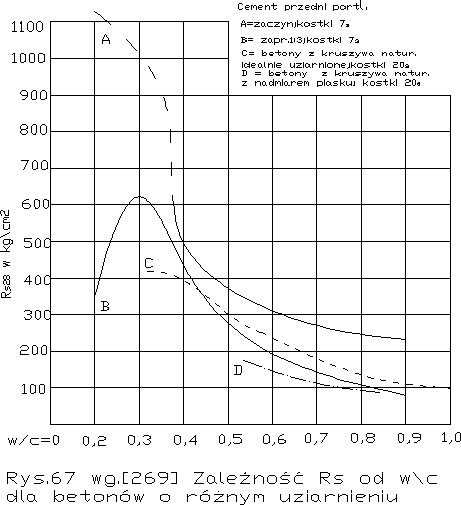
Na rys. 67 rozszerzyli Probst i Hummel swe doświadczenie odnośnie przedniego cementu portl. Jeszcze na 2 betony o tej samej zwartości cementu, ale raz z grubszym /C/, drugi raz z bardziej miałkim /D/ kruszywem, przyrównując je do zaprawy /B/ i zaczynu /A/. Zaczyn i zaprawa są te same co na rys. 66. Ponieważ zaczyn i zaprawa zbadane zostały w kostkach 73 cm betony natomiast w kostkach 20³ cm należy wytrzymałości betonów pomnożyć przez 1,15 co zresztą oznacza nieduże tylko przesunięcie krzywych C i D w górę. Po tej korekcie widzimy, że beton dobrze uziarniony C ma przy tym samym w/c wyższe R niż zaprawa B lub bardziej miałki beton D.

Dalej badali Probst i Hummel jeszcze wpływ ochudzania betonu, tj. zwiększenia ilości kruszywa (ciągle uziarnionego) w zaprawie i znaleźli wartości wg. tabl. 51. Widzimy że wpływ ochudzania jest mały i że na ogół ochudzanie wraz ze zgęstnieniem konsystencji poprawia nieco wytrzymałość. Ale zbyt daleko idących wniosków nie można z doświadczeń rys. 67 i tabl. 51 wyciągnąć.

Tabl. 51 wg. [269]
Wpływ ochudzenia na Rs przy tym samym w/c.
w/c	cement: krusz.	Rs28 w kg/cm^2	Konsyst.
0,35	1:5	420	wilg.
0,40	1:5 1:6	429 400	plast. wilg.
0,50	1:5 1:6 1:8	322 330 325	płynna plast. wilg.
0,6	1:6 1:8 1:10	225 242 241	płynna plast. gęsto-plast.
0,7	1:8 1:10	165 190	płynna plast.
0,8 0,9 1,0	1:10 1:15 1:15	145 119 102	rzadko-plast. wilg. plast.

Powyżej opisane doświadczenia zostały doskonale rozszerzone i uzupełnione doświadczeniami W. Weissgerber'a (Hiszpania) oraz A. Hummel'a. Weissgerber [268] badał również wpływ ochudzania na w/c_opt. i na Rs stosując betony z kruszywa zawierającego 44,5% piasku 0/7 i 55,5% żwiru 7/25 o składach 1:4-1:6-1:8 z cementem portlandzkim. Rezultaty mamy na rys.68.

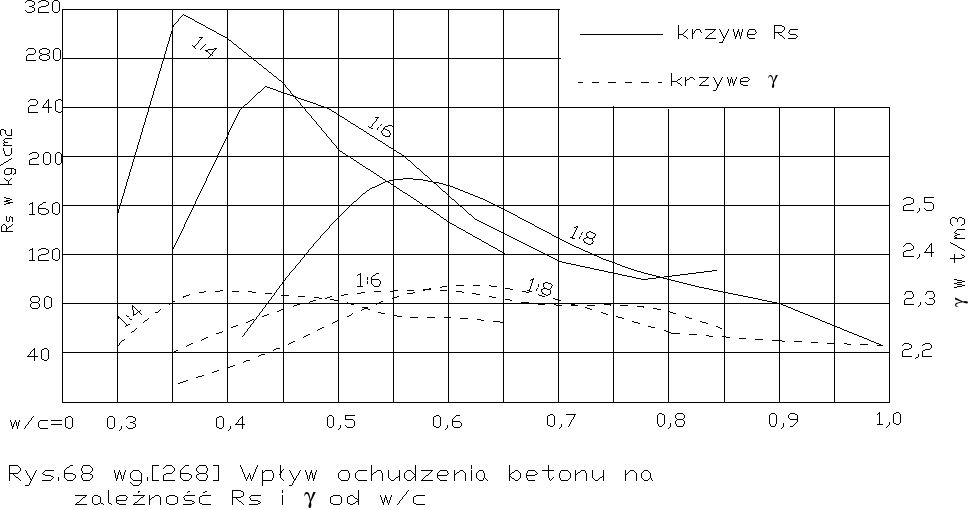
Widzimy, że optimum w/c zwiększa się ze wzrostem chudości betonu i wynosi wg. autora:

cement: krusz.	w/copt	Rs max kg/cm^2	γ	Ilośc cem. kg/m^3
1:0 1:4 1:6 1:8	0,25 0,36 0,44 0,54	552 312 256 183	2,108 2,319 2,319 2,304	1690 432 312 242

poza tym zmieniają się ze wzrostem ochudzania punkty zwrotne w linie zwrotne.- To samo widzimy na rys. 69 wg. A Hummel'a,

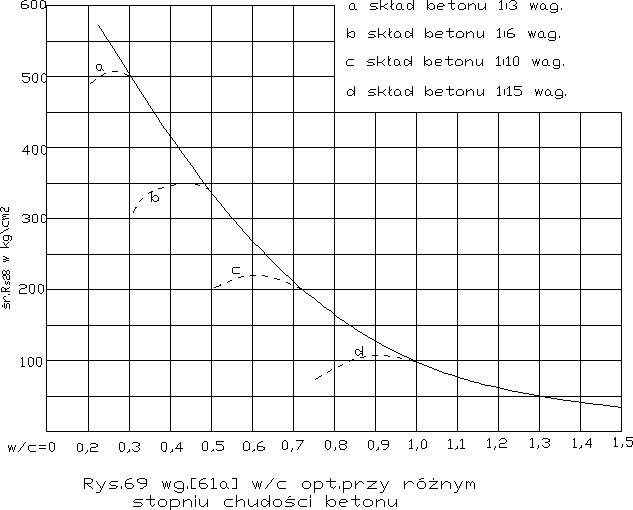
gdzie podane są optymalne w/c dla jeszcze chudszych mieszanek, a mianowicie podaje Hummel:

Dla 1:10 opt. w/c=0,62

Dla 1:15 opt. w/c=0,95

Wracając do rys. 68 widzimy, że począwszy od w/c =0,54 wytrzymałości wszystkich betonów są do siebie dosyć zbliżone i na dosyć dużym obszarze różnicę Rs mają taki charakter, że chudsze betony mają wyższą wytrzymałość analogicznie jak Probst'a i Hummel'a na tab.5.

Z wyżej przytoczonych doświadczeń możemy wyciągnąć ostatecznie następujące wnioski:

1. w/c_opt wzrasta liczbowo w miarę ochudzania mieszanki. Wynosi ono orientacyjnie dla cementów typu portlandzkiego

dla c:k =	1:0	1:3	1:5	1:6	1:8	1:10	1:15
opt. w/c=	0,20	0,3	0,4	0,45	0,55	0,65	0,95

Wzrost optimum tłumaczy się tym, że przy chudszej mieszance potrzeba więcej wody dla wytworzenia tej ilości zaczynu, która potrzebna jest do wypełniania jam kruszywa.

1. Wytrzymałość zaczynów z cementu glinowego jest przy równym w/c zawsze wyższa od wytrzymałości odpowiednich zapraw i betonów rys.66.

2. Wytrzymałości zaczynów z cementów typu portl. są przy równym w/c dla tego samego cementu wyższe od wytrzymałości zapraw i betonów, dopóki w/c<0,4 (rys. 67). Jeżeli w/c>0,4 wytrzymałość różnych mieszanek tj. zaczynów, zapraw i betonów do siebie się bardzo zbliża z tym, że przy określonym w/c i różnych stosunkach c:k zawsze istnieje jedna mieszanka, która daje najlepsze Rs. Tą mieszanką wydaje się mieszanka chudsza ale z warunkiem by w/c porównywanych mieszanek było większe od w/c_opt tej chudszej mieszanki, czyli by jamy kruszywa były przez zaczyn dostatecznie wypełnione. Całkiem pewne to twierdzenie jednak nie jest. Do sprawy chudzenia itp. wracamy w rozdz. C IV 2c.

c/ Wzory dla określania wytrzymałości.

Krzywa o kształcie jak na rys.65 nie może być wyrażona przez jednodzielny wzór matematyczny. Na szczęście jest to dla praktyki zbędne, gdyż w praktyce nie stosuje się na ogół dodatku wody mniejszego niż optymalny, a to ze względu na konieczną urabialność i ciekłość mieszanin. Zatem możemy zajmować się tylko prawą (spadającą) gałęzią krzywej rys. 65, dla której ustalenie wzoru matematycznego, określającego zależność wytrzymałości od stopnia hydratacji lub współ. w/c, jest już proste. Jest tylko pytanie co będzie wygodniejsze, czy uzależnienie wytrzymałości od stopnia hydratacji czy też od współ. w/c. Kwestia ta ma duże znaczenie dla praktyki, która wymaga, by manipulacje potrzebne do ustalenia poszczególnych wartości wzoru były proste, nie zajmowały dużo czasu i nie wymagały ani wielkiej wiedzy ani skomplikowanych urządzeń, wreszcie by wytrzymałości mogły być obliczone z właściwości podstawowych materiałów tj. cementu, wody, kruszywa.

Wzór wytrzymałości zaczynów i betonów z cementów portlandzkich, w którym wytrzymałość uzależniona jest tylko od stopnia hydratacji cementu, podał Eiger w swej pracy [9]. Wzór ten brzmi (z drobnymi zmianami w oznaczeniach) dla zaczynów:

R=2200/b^y

gdzie

R = wytrzymałość okresowa (badana)

2200 kg/cm² = wytrzymałość graniczna

b = współczynnik, zależny od kształtu ciała próbnego:

dla sześcianów 103 wynosi b=5

dla sześcianów 203 wynosi b=7

(p.rys.70)

x = w/c = współcz. wodocementowy (wagowy)

h = stopień hydratacji ≤ 1,0.

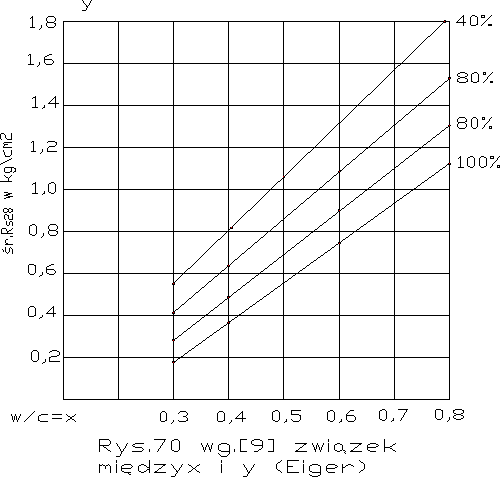
W tym wzorze nie ma żadnej wartości empirycznej prócz b, która może być dosyć ściśle raz na zawsze określona, jak to zresztą Eiger uczynił.

Dla zapraw i betonów wzór ten brzmi:

gdzie R, 2200, b, y = jak wyżej

c = ilość cementu w kg na 1 m³ betonu.

350 = zawartość cementu w betonie, który był użyty jako wzorzec.

h' = h -0,13, gdzie

h = stopień hydratacji

0,13 = stopień hydratacji niezbędny dla przejawiania minimalnej wytrzymałości betonu (por. rys.61).

Wzory Eigera teoretycznie istotnie są bez zarzutu; wytrzymałość betonu sprowadzona została poza pewnymi stałymi, które nie wymagają sprawdzenia, tylko do jednej zmiennej, a mianowicie do stopnia hydratacji h. Ta zmienna h obejmuje sobą wpływ wieku betonu, sposobu przechowywania, jakości cementu itd., jednym słowem wszystkie te czynniki które by musiały inaczej być ujęte przez współczynniki empiryczne. Dla praktyki wzór ten byłby bezcenny i ze wszystkich wzorów najściślejszy, gdyby możliwe było ścisłe ustalenie stopnia hydratacji „h” drogą obliczania go z góry. Jeżeli przejrzymy metody podane w § znajdziemy, że można ustalić bardzo dokładnie stopień hydratacji „h” ale dopiero na ciałach stwardniałych, czyli wtenczas kiedy obliczenia wytrzymałości jest już zbędne. Obliczyć wytrzymałość można byłoby natomiast tylko za pomocą krzywych rys.56. ale wtenczas dokładność rezultatów zależy już od szeregu dowolności. Mianowicie mamy tam dwie grupy krzywych między którymi trzeba wybierać lub między którymi trzeba interpolować. Następnie krzywe te miarodajne są tylko dla przechowywania wodnego , kiedy jest dość wody, by postęp hydratacji był ciągły. Zatem wzór Eigera w praktycznym stosowaniu byłby mimo wszystko obarczony szeregiem niedokładności, nie mówiąc o niedogodności w postaci ustalania uziarnienia cementu, które wymaga pracowników o wysokich kwalifikacjach specjalnych.

Wzory stosowane w praktyce oparte są na współ. w/c i zawierają współczynniki empiryczne, które mogą być ustalane przez każdego pracownika umysłowego. Z naukowego punktu widzenia wory oparte na w/c mają tę ujemną stronę że przy uzależnieniu wytrzymałości od współ w/c uwzględniony być musi czas, gdyż do jednego współ. w/c należą w czasie różne wytrzymałości, zatem otrzymujemy inne krzywe zależności dla wytrzymałości 3-dniowej, inne dla 7- i 28-dniowej. Poza tym musimy znać jakość cementu, gdyż każdy cement ma swoją wytrzymałość normalną, zmienną zresztą zależnie od przechowania. Przy stosowaniu współczynnika w/c musimy więc wprowadzać szereg współczynników więcej lub mniej empirycznych, których dokładność przeważnie bywa zupełna. Ale w praktyce przedstawia się sprawa mniej kłopotliwie. Na budowie operuje się zazwyczaj tylko jednym gatunkiem cementu. Jeżeli się dla tego cementu raz na zawsze ustali doświadczalnie wspomniane współczynniki jakości cementu, czasu twardnienia, sposobu przechowania itd. tak, że pozostaje tylko ustalenie współ. w/c, wtenczas manipulacja wzorami staje się niezmiernie prostą.

Wzorów opartych na w/c istnieje kilka. Omawiamy je w rozdziale C, gdyż wprowadzone były dla zapraw i betonów i służą w pierwszym rzędzie potrzebom praktyki budowlanej.

4. Inne wytrzymałości

1. Rozciąganie i zginanie

Wszystko co mówiliśmy o wpływie stopnia hydratacji, porowatości i współ. w/c na wytrzymałość na ściskanie Rs dotyczy również wytrzymałości na rozciąganie Rr z tą różnicą, że wytrzymałość na rozciąganie jest kilka do kilkunastu razy niższa, niż na ściskanie. Różnica ta daje się również wytłumaczyć właściwościami stwardniałego gelu. Jak już zaznaczyliśmy, gel nie jest materiałem jednolitym, a składa się z ciał krystalicznych i ciał bezpostaciowych. Na powierzchniach styku kryształków ze sobą lub z ciałami bezpostaciowymi kohezja gelu nie może oczywiście być taka duża jak w samym wnętrzu kryształków. Przy ściskaniu następuje zbliżanie się cząstek, czyli ściskanie działa w kierunku sił molekularnych; jest zatem zasadniczo bez różnicy, czy są one ze sobą spojone czy też nie. Przy rozciąganiu natomiast naprężenia działają w kierunku przeciwnym sił i wtenczas gel pęka w punktach lub powierzchniach najsłabszego ich działania, czyli na powierzchni kryształków. Do tego rodzaju słabych miejsc dochodzi zapewne jeszcze wpływ submikroskopijnych próżni powstałych właśnie na tych powierzchniach styku wskutek lekkiego nadmiaru wody, który przy krystalizacji wypierany bywa na zewnątrz kryształów, oraz wskutek opóźniania tworzenia się niektórych związków w stosunku do innych, dalej wewnętrzne pęknięcia zaczynu osłabiają daleko więcej wytrzymałość na rozciąganie, niż na ściskanie.

Wytrzymałość na rozciąganie ma jak wytrzymałość na ściskanie również swą optymalną ilość wody zarobowej. Przykład zależności Rr, od w/c mamy wg. Probsta i Hummela [269] na rys. 71, który jest odpowiednikiem rys.66.

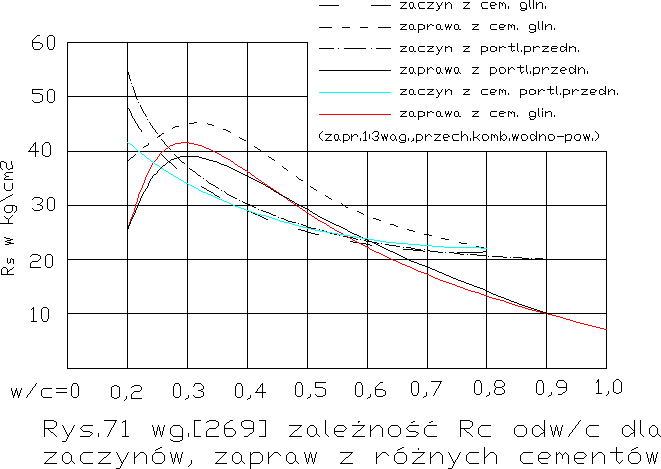
Widzimy, że w/c_opt wynosi dla zaczynu ~0,2 dla zaprawy 1:3~0,3 jak w ściskaniu. Ale poza tym różnice między Rr zaczynów i zapraw są mniejsze, jak również mniejsza jest wrażliwość Rr na rozrzedzenie betonu. Przy wyższym w/c spada Rr mniej niż Rs, lub inaczej mówiąc, stosunek Rr/Rs jest tym liczbowo większy im słabszy jest beton. Poza tym są wytrzymałości Rr wszystkich trzech cementów są do siebie znacznie bardziej zbliżone. Naturalnie wzrasta wytrzymałość na rozciąganie również ze stopniem hydratacji jak widzimy na rys. 72 wg A. Eigera [3]. Wg Wernera i Hedstroma [131], istnieje analogicznie jak dla ściskania (rys.60) zależność Rr od objętości trwałej substancji f w % w zaczynie, wg wzoru

Rr = 0,224 (f-25) ^4/3

co ponownie dowodzi, że jakość cementu w większości sprowadzona być może do szybkości hydratacji. Ale ciekawszy jest pokazany na rys. 72 związek między Rr i Rs.

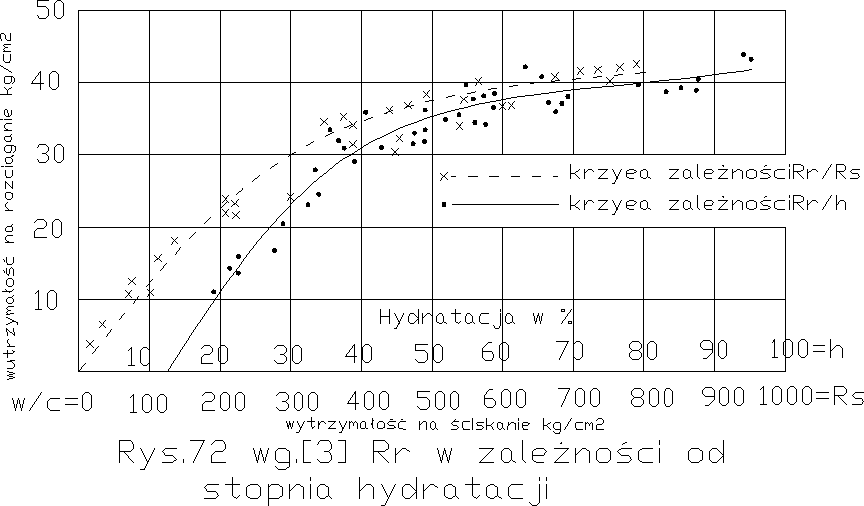
Zależność między nimi jest tak prawidłowa, że niewątpliwie te same czynniki, które podwyższają Rs, podwyższają z reguły również Rr. Poza tym jednak przyrost Rr w rys. 72 tak samo jak w rys. 71 jest tym mniejszy, im większe jest przynależne Rs. Związek między Rr i Rs bez względu na wiek, przechowywanie itp. Możemy wg. Fereta wyrazić wzorem

Rr = α * Rs ^2/3

Wzór ten daje przy α = 0,66 bardzo dobrą zgodność z doświadczeniami rys. 72 w granicach od Rs=0→400 kg/cm² , dla wyższych Rs wartości wyliczone tym wzorem są za wysokie. Dla różnych cementów jest zresztą α nieco różne.

Dla zapraw normowych (za 33 lata badania) podaje Haegermann [236] wzór dla przechowania wodnego

a dla przechowania w wilgotnym powietrzu o 10 kg/cm² więcej i to również bez względu na wiek.

Naturalnie nie stosuje się Rr ściśle do powyższych wzorów a zachodzą odchylenia i to niekiedy poważniejsze. Ale przyczyn odchyleń nie udało się dotychczas nawet w pierwszym przybliżeniu ustalić. Wiadomo tylko, że bardzo duże odchylenia następują wówczas , jeżeli i spoiwo ma skłonność do lekkiego pęcznienia. Takie pęcznienie nie widoczne dla oka obniża Rr podwyższając jednocześnie Rs (ukryte pęcznienie)

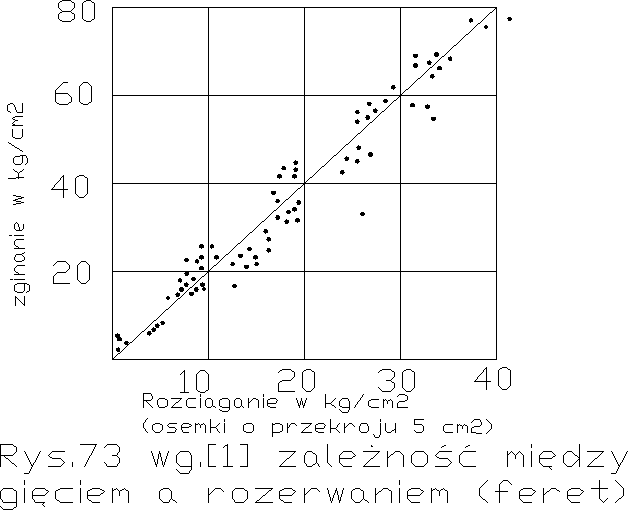
To, co powiedziano wyżej o rozciąganiu (osiowym) dotyczy również zginania, gdyż przy zginaniu betonu miarodajna jest wytrzymałość na rozciąganie. Naprężenia przy zginaniu oblicza się zakładając z Nawierem, że naprężenia rozciągające i ściskające rosną proporcjonalnie do odległości włókien od osi obojętnej. Dla kamieni i betonów założenie to jest niesłuszne, wzrost naprężeń rozciągających jest mniejszy. Wskutek tego otrzymujemy przy zginaniu inną wytrzymałość (ok.2-kr-wyższą) niż przy rozciąganiu osiowym wg rys. 273 [1] Fereta. Poza tym jednak związek między rozciąganiem od zginania a rozciąganiem osiowym jest, jak widzimy czysto liniowy, a w stosunku do ściskania wynosiłoby

S. Giertz-Hedstrom [233] podaje

Na rys. 74 wg. Grafa ¹)mamy przykład zależności Rzg od Rs dla zapraw normowych z nowszych cementów. Widzimy, że również Rzg dąży do określonej granicy, która leży nieco wyżej 10 kg/cm².

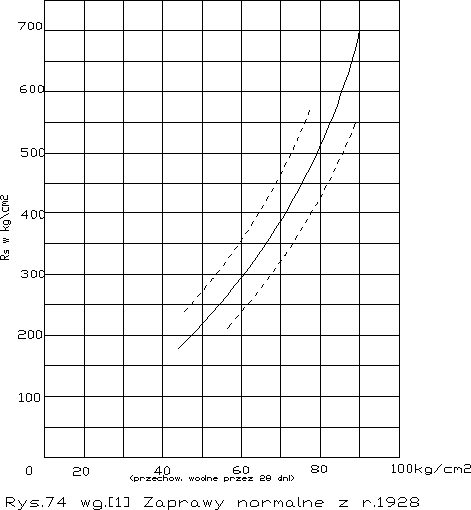
Mała wytrzymałość na rozciąganie jest w ogóle słabą i w pewnym sensie niebezpieczną stroną spoiw, a w szczególności cementów. Wywodzenie jej z właściwości gelu dowodzi, że jest to wada nieusuwalna. Istotnie usiłowania podniesienia wytrzymałości na rozciąganie spełzły na niczym i wyniki jednego kongresu poświęconego temu tematowi były nader nikłe. O ile możliwości podwyższenia wytrzymałości na ściskanie nie są jeszcze wyczerpane, o tyle wytrzymałości na rozciąganie nawet przy znacznym podwyższeniu Rs stoją jakby w miejscu i stosunek Rr:Rs jest tym mniejszy, im mocniejszy jest cement.

Jeżeli chodzi o stosunek Rr/Rs u różnych rodzajów cementów to mamy niektóre dane dla zapraw normowych na tabl. 52 wg. R.Burchartza [50]. Podajemy te liczby bez komentarzy, zwracając tylko na to uwagę, że dotyczą one zapraw normowych , a więc zapraw o Rs= 400→600 kg/cm².

Dla realnej oceny różnych rodzajów cementów nie mogą one służyć, gdyż są zbyt niepewne i nie bardzo zgadzają się z danymi rozdz. A IV dla poszczególnych cementów - Wg Gruna [47a] cementy ubogie w wapno odznaczają się na ogół większą wytrzymałością na rozciąganie. - A. Guttmann [307] twierdzi, że cementy glinowe mają wyższe Rr niż cementy portlandzkie.

Jeżeli chodzi jeszcze o cementy portlandzkie, to musimy odróżnić cementy z przed kilkudziesięciu lat od cementów obecnych. Na skutek stałego powiększania Rs spadł średni stosunek Rr/Rs z

gdyż jednoczesne powiększenie Rr okazało się niemożliwe [307].

Tabl.52 wg [50] stosunek Rr : Rs u zapraw normowych z różnych cementów
Gatunek cementu	Stosunek Rr : Rs Przy przechowaniu			Wytrzymałość R28 w % przy R7=100%
		wodnym		komb. wodno-pow.	Rr28 przechow.		Rs28 przechow.
		7 dn.	28 dn.	28 dn.	wodne	komb.	wodne.	komb.
cem. portl. przedni c.portl. cem. żelazisty cem. wielkop. cem. glinowy				125 111 124 132 106	167 142 158 144 143	139 123 138 144 125	164 140 159 167 133

b/ Sprężystość

Sprężystość zaczynu jako materiału praktycznie homogenicznego zależy oczywiście tylko od porowatości zaczynu. Werner i Hedstrom [131] podają tu zależność wg rys. 75 i wzoru

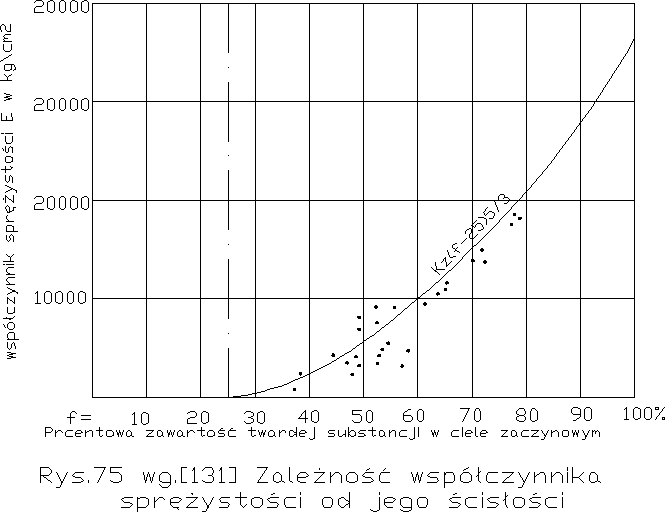
E= 254* (f-25)^5/3

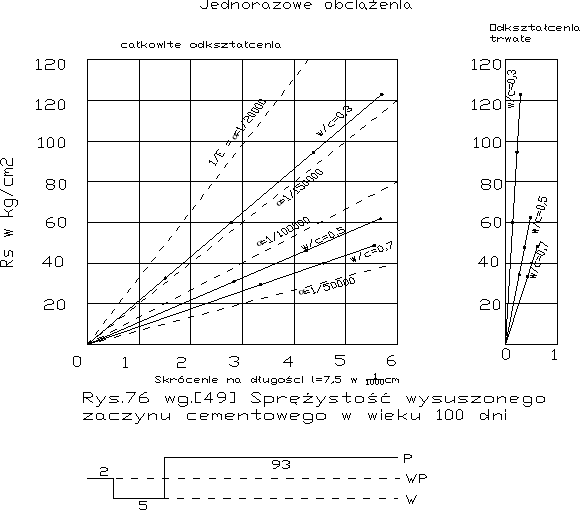
gdzie f= objętość trwałej substancji w zaczynie w % , analogicznie jest dla ściskania i rozciągania. Zależność sprężystości zaczynu od w/c widzimy na rys. 75 wg. doświadczeń Grafa [49]. Dla w/c=0 wynosi np. współczynnik sprężystości po 100 dniach E= ~60000 kg/cm². Odkształcenia trwałe przy jednorazowym obciążeniu są stosunkowo nikłe. W danym wypadku zaczyn był praktycznie zupełnie zhydratyzowany. Sprężystość może zresztą być związana z wytrzymałością na ściskanie Rs i na rozciąganie Rr wg następującego wzoru Wernera i Giertz-Hedstroma [233].

c/ Ścieralność

W pewnym związku z wytrzymałością na ściskanie i rozciąganie stoi również ścieralność. Z zaczynami mamy kilka doświadczeń, ale tylko odnośnie wpływu w/c , porównania różnych cementów w postaci zaczynów nie ma, choć byłoby ciekawe dowiedzieć się, w jakim np. stopniu dla ścierania wpływ jakości cementu sprowadzony być może do ilości twardej substancji w zaczynie i ścisłości na wzór rys. 60 i 75.

Ścieralność zaczynu o różnym w/c została zbadana przez A. Szumana [98] na kostkach 7,07 cm, ubijanych aparatem Martens-Bohme'go 150 uderzeniami, przechowywanych komb. wodno-pow., po uprzednim starciu górnej warstwy przy 110 obrotach i ścieraniu na tarczy Bohmego 440 obrotami. Rezultaty podane są na tabl. 53. Widzimy, że mimo dużych różnic w wytrzymałościach, ścieralność zaczynów w badanych granicach w/c= 0,2→0,3 była prawie jednakowa i niezależna od w/c.

Tabl. 53 wg [98] Ścieralność zaczynu cementowego (tarcza Bohme'go 440 obrotów)
Wytrzymałość	Zaczyn o w/c =
		0,2	0,25	0,30
Rs3 Rs7 Rs28 Rr28	502 648 822 55,2	432 608 738 47	272 495 620 28,4
Ścier. po 28 dn. cm^3/cm^2	0,348	0,360	0,360

Dla wyższych w/c=0,5→1,0 badał ścieralność zaczynów Brandt [1]. Rezultaty widzimy na rys. 77 .

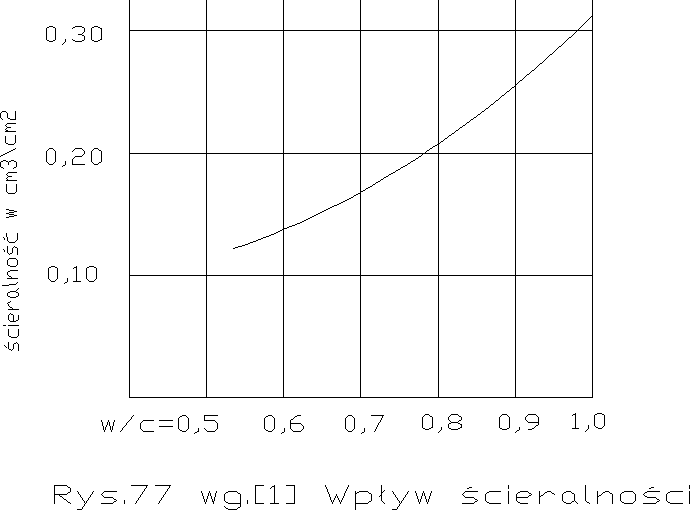
Tutaj jest zależność ścieralności od w/c wyraźna , ale widzimy zarazem, że przy niższym w/c krzywa dąży do poziomej, czyli różnice ścieralności są tym mniejsze, im mniejsza jest w/c, co się pokrywa z doświadczeniami Szumana. Różnice liczbowe między autorami są tu nie istotne, bo każdy z nich badał inny cement i zapewne inną metodą.

Badania ścieralności zaczynów mają zresztą dla technologii betonu o tyle mniejsze znaczenie, że przy ścieraniu betonu największy opór stawiają ziarna kruszywa jako z reguły o wiele twardsze od zaczynu. Zadaniem zaczynu jest głównie należyte spojenie ziaren kruszywa, a nie samodzielny opór ścierania, o czym w rozdz. C.

5. Ciężar gatunkowy zaczynu.

Dla ustalenia ciężaru gatunkowego zaczynu musimy odróżnić stan świeży i stan po stężeniu.

α. Świeży zaczyn. Ciężar gatunkowy świeżego zaczynu jest wypadkową ciężarów gatunkowych cementu i wody. Ciężar gatunkowy możemy dla dowolnego w/c obliczyć zakładając, że objętość zaczynu równa się objętości jego składowych części, tj. absolutnej objętości cementu plus objętość wody. Takie założenie jest zupełnie dopuszczalne, tak np. otrzymano doświadczalnie z 1,68 kg cementu + 0,437 litrów wody dokładnie 1 litr stwardniałego zaczynu, czyli dla γc =3,1, było

195

---