1.Wstęp
Celem ćwiczenia jest doświadczalne wyznaczenie momentów bezwładności brył obrotowych oraz środków ciężkości brył nieregularnych. Zakres materiału teoretycznego niezbędny do zrozumienia ćwiczenia obejmuje: analityczne wyznaczenie masowych momentów bezwładności brył obrotowych względem osi, drgania swobodne układów dyskretnych o jednym stopniu swobody, kinematykę i dynamikę bryły sztywnej w ruchu obrotowym.
W ćwiczeniu otrzymamy momenty bezwładności wybranych brył obrotowych dwiema metodami (Część I i II) oraz położenie środka ciężkości kilku brył nieregularnych (Część III).
2.Tok obliczeń
CZĘŚĆ I.
W tej części ćwiczenia wykorzystaliśmy stanowisko pomiarowe przedstawione na poniższym schemacie
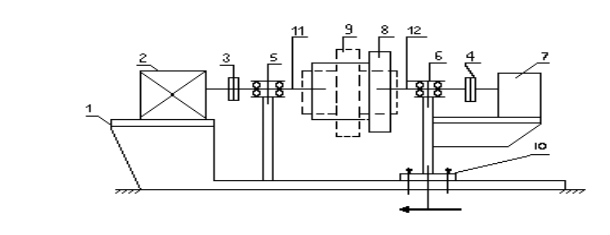
Stanowisko składa się z:
1- ramy, 2- silnika elektrycznego, 3- sprzęgła I, 4- sprzęgła II, 5- podpory łożyskowej wału, 6- przesuwnej podpory łożyskowej wału, 7- licznika obrotów, 8- przedmiotu badanego, 9- śrub umożliwiających ruch podpory
Obliczenia dla bryły (bryła wzorcowa)
Bryła składa się z trzech walców z wydrążonym otworem
h1=18mm; h2=40mm; 1 = 20mm; = 57mm; = 130mm;
Obliczenie masy
m = m1 + m2 + m3 - m4
m1 = m3 - masa walca I =ρ R22 H1= 7,86.103.3,14.(0,0285)2.0,018= 0,36 kg
m2 - masa walca II =ρ R3 2 H2= 7,86.103.3,14.(0,065)2.0,04= 4,170 kg
m4 - masa wydrążonego otworu =ρ r2 ( H1+H2+H3)= 7,86.103.3,14.(0,01)2.0,076 = 0,18 kg
m= 4,7 kg
Obliczenie przyspieszenia kątowego
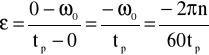
(znak minus oznacza, że jest to przyspieszenie hamujące)
= -15,118 rad / s2
= -15,430 rad / s2
= -15,590 rad / s2
-15,590 rad / s2
-15,118 rad / s2
-15,272 rad / s2
-14,819 rad / s2
-14,673 rad / s2
-14,967 rad / s2
-15,118 rad / s2
εśr=-15,1695 rad / s2
Obliczenie analitycznego momentu bezwładności
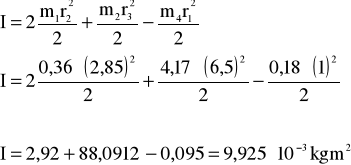
Obliczenie momentu hamowania M
M=(I+Iw)•ε
M=(9,925+0,157)•15,1695
M=15,29•10-2 Nm
Lp. |
Prędkość obrotowa no |
Czas wybiegu tp |
Analityczny moment bezwładności I |
Moment hamowania M |
1 2 3 4 5 6 7 8 9 10 |
1430 1430 1430 1430 1430 1430 1430 1430 1430 1430 |
9,9 9,7 9,6 9,6 9,9 9,8 10,1 10,2 10,0 9,9 |
9,925 . 10-3 |
15,29 . 10-3 |
CZĘŚĆ II.
Schemat stanowiska pomiarowego
Stanowisko składa się z: stojaka 1, cięgien 2, tarczy 3 i bryły o nieznanym momencie bezwładności.
Po doświadczalnym wyznaczeniu okresu drgań tarczy z bryłą (T), określiliśmy na podstawie poniższego wzoru nieznane momenty bezwładności brył

Nr pomiaru |
Ciężąr tarczy Q 0 i bryły Q [ N ] |
Długość linki i promień tarczy |
Czas 10 wahnięć tarczy [s] |
Czas 10 wahnięć tarczy z bryłą |
Okres T0 [ sek ] |
Okres T [sek ] |
Moment bezwładności .10 -3 [ kgm2] |
1 |
Q 0 = 24.77 |
l = 0.63 m |
5,6 |
3,4 |
0.56 |
0.34 |
3,4727 |
2 |
Q = 46.10 |
r = 0.15 m |
5,7 |
3,6 |
0.57 |
0.36 |
4,4915 |
3 |
|
|
5,6 |
3,7 |
0.56 |
0.37 |
5,4084 |
wartość śr. |
|
|
5,6 |
3,5 |
|
|
4,4575 |
Wyniki obliczeń zamieszczone są w tabelce.
CZĘŚĆ III.
Schemat stanowiska pomiarowego
Elementy składowe stanowiska: 1- stojak, 2- skala kątowa, 3- obciążnik, 4- cięgna, 5- bryły o nieznanym położeniu środka ciężkości.
Nr bryły |
Ciężar obciąż. Q [N] |
Ciężar bryły G [N] |
Kąty wyznaczone przez cięgno (a) p k |
| k - p| |
h [m] |
a [m] |
|
|
|
|
|
|
|
1 |
5,197 |
19,612 |
14 20 |
6 |
0,266 |
0,105 |
|
|
|
|
|
|
|
Obliczenia środka ciężkości
Bryła 1
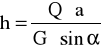
[m]
*
a = 0.105 m;
mbryły = 2 kg
G = 19.612 N;
mobciążnika=0,53 kg 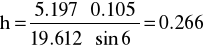
[m]
Q = 5.197 N;
3. Wnioski
Tabela wyników
Analityczny moment bezwł. [kgm2] |
Moment bezwł. z Części I ćw. [kgm2] |
Moment bezwł. z części III ćw. [kgm2] |
|
|
|
|
|
9,925 * 10 - 3 |
9,9246 * 10 - 3 |
4,4575 * 10 - 3 |
|
|
|
|
|
Wyniki otrzymane z pomiarów przeprowadzonych w ćwiczeniu różnią się od wyników analitycznych. Różnice te wynikają z małej dokładności pomiaru brył oraz czasu. Mimo takich różnic, ćwiczenie zostało wykonane prawidłowo, a wyniki uważamy za poprawne.
2
Wyszukiwarka
Podobne podstrony:
Momenty bezw, PW Transport, Gadżety i pomoce PW CD2, MECHANIKA, mechanika techniczna - laboratoria,
momentu, PW Transport, Gadżety i pomoce PW CD2, MECHANIKA, MECHANIKA !!, mechanika techniczna - labo
TARCIE, PW Transport, Gadżety i pomoce PW CD2, MECHANIKA, MECHANIKA !!, mechanika techniczna - labor
kiossdobry, PW Transport, Gadżety i pomoce PW CD2, płytki, Technologia wytwarzania
Cw 10 NASZE3, PW Transport, Gadżety i pomoce PW CD2, MECHANIKA, Mechanika~1!!!
Spawanie, PW Transport, Gadżety i pomoce PW CD2, płytki, Technologia wytwarzania
Badanie odbicia światła od powierzchni dielektryków, PW Transport, Gadżety i pomoce PW CD2, płytki,
sprawo 24, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, od Marka, Fizyk
Spawalnictwo, PW Transport, Gadżety i pomoce PW CD2, płytki, Technologia wytwarzania
Cwiczenie 1 lab fiz, PW Transport, Gadżety i pomoce PW CD2, płytki, ChujWieCo, fizyka, fizyka, spraw
więcej podobnych podstron