Politechnika Rzeszowska

im. Ignacego Łukasiewicza

Katedra Informatyki i

Automatyki

Sztuczna inteligencja

Sieci neuronowe -projekt

Temat: Zrealizować sieć neuronową uczoną algorytmem wstecznej propagacji

błędu z przyspieszeniem metodą adaptacyjnego współczynnika

uczenia (trainbpa) uczącą się predykacji zestawu kart w grze Poker

Autor:

Łukasz Stojak

L 10, 2 EF-DI

Spis treści

Spis treści ………………………………………………………………………………….. 2

Wstęp ………………………………………………………………………………………. 3

Specyfikacja danych wejściowych ……………………………………………………... 3

Sztuczne sieci neuronowe ………………………………………………………………. 4

Realizacja sieci neuronowej w programie Matlab 7.1 …………………………………6

Eksperymenty ………………………………………………………………………………10

Podsumowanie …………………………………………………………………………….

Wstęp

Tematem projektu jest: „ realizacja sieci neuronowej uczonej algorytmem wstecznej propagacji błędu z przyspieszeniem metodą adaptacyjnego współczynnika uczenia (trainbpa) uczącą się predykacji zestawu kart w grze Poker” . Za zbiór danych zastosowany do uczenia sieci przyjęto dokument opublikowany na stronie http://archive.ics.uci.edu/ml/datasets/Poker+Hand. W pliku znajdują się dane dotyczące rozdań kart w grze Poker. Sieć ma za zadanie przewidywać te rozdania. Aby to było możliwe musi posiąść odpowiednią wiedzę na ten temat, którą stanowią rozdania kart. Do realizacji projektu wykorzystano środowisko Matlab 7.1 oraz pakiet NeuralNetworkToolbox.

Specyfikacja danych wejściowych

Charakterystyka danych:

Charakterystyka zbioru danych: wiele zmiennych
Liczba przypadków: 1025010
Strefa: Gra
Charakterystyka atrybutów: Kategorie, liczby całkowite
Liczba atrybutów: 11
Data przekazania: 2007-01-01
Powiązanie zadań: Klasyfikacja
Brakujące wartości? Nie

Źródło danych:

Carleton University, Department of Computer Science
Intelligent Systems Research Unit
1125 Colonel By Drive, Ottawa, Ontario, Canada, K1S5B6

W grze poker używana jest talia 52 kart. Każda z tych kart opisana jest dwoma atrybutami tzw. kolorem i figurą. Dane użyte do uczenia sieci posiadają następujące wartości liczbowe dla tych atrybutów.

Kolor:

1 - odpowiada kier

2 - odpowiada pik

3 - odpowiada karo

4 - odpowiada trefl

Figura:

1. odpowiada As

2. odpowiada 2

3. odpowiada 3

4. odpowiada 4

5. odpowiada 5

6. odpowiada 6

7. odpowiada 7

8. odpowiada 8

9. odpowiada 9

10. odpowiada 10

11. odpowiada Walet

12. odpowiada Dama

13. odpowiada Król

Każde z rozdań składa się z 5 kart, gdzie ich kolejność ma znaczenie. Wynika z tego, że ułożenie kart w rozdaniu określa typ rozdania. W grze Poker występuje 10 typów rozda, które posiadają swój ranking.

Klasyfikacja rozdań:

0. Nic ( rozdanie nie kwalifikujące się do poniższych )

1. Jedna para ( para kart z tą samą figurą )

2. Dwie pary ( dwie pary kart z tą samą figurą )

3. Trójka ( trzy karty z tą samą figurą )

4. Strit (pięć kart ułożonych kolejno według figury )

5. Kolor ( pięć kart w tym samym kolorze )

6. Ful ( trójka i para )

7. Kareta (cztery karty z tą samą figurą )

8. Poker ( strit w jednym kolorze )

9. Poker królewski (dziesiątka, walet, dama, król, As - wszystko w jednym kolorze)

Przyjmijmy, że K - numer koloru, F - numer figury, T - numer typu rozdania. Wtedy każde rozdanie zakodowane będzie w następujący sposób: K1,F1,K2,F2,K3,F3,K4,F4,K5,F5,T. Przykładowo rozdanie zakodowane w następujący sposób: 4,13,2,10,1,10,3,7,2,10,2 oznaczać będzie kolejno Króla trefl, dziesiątkę pik, dziesiątkę kier, siódemkę karo, a typ rozdania to dwójka.

Dla poprawności procesu uczenia zakodowane w ten sposób dane poddano procesowi normalizacji. Pierwsze 10 kolumn to dane wejściowe, natomiast 11 kolumna to oczekiwana odpowiedź.

Sztuczne sieci neuronowe

Sztuczna sieć neuronowa jest tworem mającym za zadanie jak najbardziej odzwierciedlać naturalną sieć neuronową, która jest częścią układu nerwowego człowieka. Sieci neuronowe to nowoczesne systemy obliczeniowe bazujące na zjawiskach zachodzących w mózgu.

Za pomocą sieci neuronowych można zamodelować takie funkcje jak:

• Przewidywanie (predykacja) - czyli przewidywanie danych wyjściowych na podstawie danych wejściowych, które sieć wykorzystywała w procesie uczenia. Występuje tu analogia do mózgu człowieka, który potrzebuje danych wzorcowych tylko do nauczenia się ich

• Klasyfikacja i rozpoznawanie - poprzez nauczenie sieci pewnych cech charakterystycznych możliwe jest, aby sieć sposób interaktywny rozpoznała i zakwalifikowała sygnał wejściowy.

• Kojarzenie danych - Sieć potrafi skojarzyć dane wyjściowe podstawie danych wejściowych, które po nauczeniu sieci mogą się mniej lub bardziej różnić od danych wzorcowych. Sieć oblicza więc swój współczynnik korelacji między danymi wejściowymi a nauczonym wzorcem. W zależności od wartości tego współczynnika sieć dokonuje kojarzenia danych.

• Analiza danych - To właściwość za pomocą której sieć potrafi znaleźć związek między danymi wejściowymi .

• Filtracja sygnałów - Funkcja filtrów o dowolnym zakresie przepustowości. Ta cecha pozwala wyeliminować sygnały, będące szumami, Sieć taka doskonale filtruje dane które nie należą do grupy reprezentujących pomiar, mają charakter stochastyczny . Nauczona sieć w zadziwiający sposób radzi sobie z filtracją, bo w sposób “inteligentny” przepuszcza sygnały do dalszej analizy, z czym nie radziły sobie zwykłe filtry.

• Optymalizacja - To cecha która pozwala na dokonywanie analizy danych i kojarzenia najlepszych z pośród możliwych rozwiązań.

Opisane wyżej cechy prawie nigdy nie występują pojedynczo. Sieć zaprojektowana do konkretnego zastosowania zazwyczaj posiada kilka tych własności. Wykorzystanie ich pozwala stworzyć doskonałe urządzenia.

Zaletami sztucznych sieci neuronowych jest brak konieczności oprogramowywania, zdolność do uogólniania nabytej wiedzy oraz wysoka odporność na naruszenie jej struktury. Aby stworzyć poprawnie działającą sieć wystarczy ją zaprojektować i sterować procesem uczenia. Wadami sieci jest to że nie dostarczają nam one precyzyjnych wyników co wyklucza je z zadań obliczeniowych. Nie nadają się także do rozwiązywania problemów wymagających myślenia wieloetapowego.

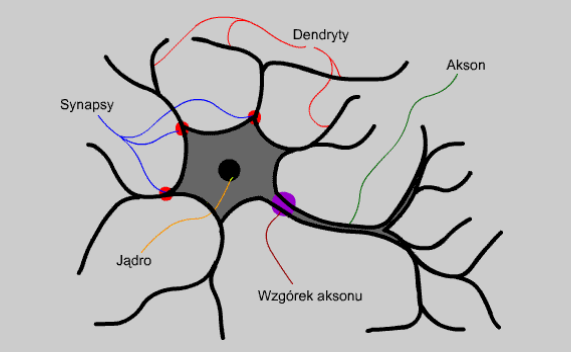
Sieci neuronowe wzorowane są na naturalnym modelu neuronu. Model ten, zarówno jak i model sztucznego neuronu przedstawiono na rysunkach poniżej.

Rys 2 Model sztucznego neuronu

Rys 1 Model naturalnego neuronu

• Jądro - stanowi "centrum obliczeniowe" neuronu. To tutaj zachodzą procesy kluczowe dla funkcjonowania neuronu. W sztucznym neuronie odpowiada ono blokowi sumującemu.

• Akson - jest to wyjście neuronu za pomocą, którego powiadamia on świat zewnętrzny o swojej reakcji na dane wejściowe. Neuron posiada tylko jeden akson. Odpowiednik wyjścia.

• Wzgórek aksonu - stąd wysyłany jest sygnał wyjściowy, który wędruje dalej poprzez akson. Jego odpowiednikiem jest blok aktywacji.

• Dendryt - "wejście" neuronu. Tędy trafiają do jądra sygnały mające być w nim później poddane obróbce. Dendrytów może być wiele - biologiczne neurony mają ich tysiące.

Na rysunku sztucznego neuronu dendrytowi odpowiadają wejścia.

• Synapsa - jeśli dendryt jest wejściem neuronu, to synapsa jest jego furtką. Może ona zmienić moc sygnału napływającego poprzez dendryt. Odpowiednikami synaps, a ściślej modyfikacji przez nie dokonywanych w sztucznym neuronie są wagi.

Połączone neurony tworzą sieć. Nawet jeden neuron można uznać za sieć - jednoelementową. Aby móc jednak używać sieci do bardziej złożonych zadań należy użyć większej ilości neuronów. Neurony połączone ze sobą tworzą warstwy. W większości zastosowań budujemy siec złożoną z jednej, dwu lub trzech warstw, gdyż zastosowanie większej ich liczby nie ma praktycznie sensu. Neurony leżące w jednej warstwie nie są między sobą połączone, natomiast należące do różnych warstw są połączone według zasady każdy z każdym. Sieć wielowarstwową przedstawiono na rysunku poniżej.

Rys 3 Sieć wielowarstwowa

Na rysunku widać, że sieć posiada jeszcze jedną warstwę zwaną warstwą wejściową. Służy ona do wstępnej obróbki danych wejściowych. I tu muszę powiedzieć choć parę słów o działaniu sieci. Do każdego z neuronów w warstwie pierwszej trafia każdy z sygnałów wejściowych podanych przez użytkownika. Neurony przetwarzają sygnały wejściowe i podają poprzez swoje wyjścia na wejścia neuronów następnej warstwy. To, co pojawi się na wyjściach neuronów warstwy ostatniej (wyjściowej), jest wynikiem działania sieci.

Rozróżniamy sieci jednokierunkowe i rekurencyjne, w których dodatkowo występuje sprzężenie zwrotne. Za jego pośrednictwem sygnały mogą po przejściu danej warstwy wracać na jej wejście, zmieniając przy tym swoje wartości, co powtarza się wiele razy, aż do osiągnięcia pewnego stanu ustalonego.

Realizacja sieci neuronowej w programie Matlab 7.1

Do realizacji sztucznej sieci neuronowej wykorzystującej metodę trainbpa użyto środowiska Matlab w wersji 7.1. Poniżej zamieszczony został kod którego użyto do stworzenia, nauczenia i przetestowania działania sieci neuronowej.

Skrytp sieci trójwarstwowej

clear all nntwarn off format long load poker_norm [wiersze,kolumny]=size(Pnew); dane=100 S1=20 S2=10 przesk=0.05; start=100; do_err=0.25 err_goal=start; for i = 1:1:1000 do_spr(:,i) = Pnew(:,i) end for i = 1:1:1000 TT(i) = T(i) end ilosc=(ceil(length(Pnew)/dane)*przesk) zmiana=((start-do_err)/ilosc); [w1,b1,w2,b2,w3,b3]=initff(Pnew,S1,'tansig',S2,'tansig',T,'purelin'); for y=1:ilosc ind=ceil(rand(1,dane)*length(Pnew)); Pm=zeros(wiersze,dane); Tm=zeros(1,dane); for i=1:dane, Pm(:,i)=Pnew(:,ind(i)); Tm(:,i)=T(:,ind(i)); end for g=1:1000, for z=1:10, if max(Pm(z,:))==min(Pm(z,:)) ind=ceil(rand(1,dane)*length(Pnew)); Pm=zeros(wiersze,dane); Tm=zeros(1,dane); for i=1:dane, Pm(:,i)=Pnew(:,ind(i)); Tm(:,i)=T(:,ind(i)); end z=1; end end end y ilosc zmiana disp_freq=500; max_epoch=10000; if err_goal>do_err err_goal=err_goal-zmiana; else err_goal=do_err; end lr=0.01; err_goal tp=[disp_freq,max_epoch,err_goal,lr]; [w1,b1,w2,b2,w3,b3,TE,TR]=trainbpa(w1,b1,'tansig',w2,b2,'tansig',w3,b3,'purelin',Pm,Tm,tp); plot(TR) plot(ne) end A3=simuff(do_spr,w1,b1,'tansig',w2,b2,'tansig',w3,b3,'purelin'); kd=(1-( (sum( abs(TT-A3) >0.5))/length(do_spr) ) )*100

Opis skryptu

Skrypt rozpoczyna się do linijek które wykonują następujące funkcje:

1 clear all 2 nntwarn off 3 format long 4 load poker_norm

- czyści przestrzeń roboczą

- wyłącza ostrzeżenia

- wczytuje plik ze znormalizowanymi danymi

Kolejne linijki kodu to ustawienia odpowiedzialne za konfigurację sieci i procesu uczenia

5 dane=10000 6 S1=20 7 S2=10 8 przesk=1; 9 start=100; 10 do_err=0.25;

-liczba losowo wybieranych wierszy

- liczba neuronów w warstwie pierwszej

- liczba neuronów w warstwie drugiej

- odpowiada za ilość kroków

- startowy err_goal

- końcowy err_goal

Pętle służące do pobrania danych sprawdzających stopień nauczenia się sieci.

11 for i = 1:1:1000 12 do_spr(:,i) = Pnew(:,i) 13 end 14 for i = 1:1:1000 15 TT(i) = T(i) 16 end

Dane pobierane są do tablicy do_spr. Stopień nauczenia się sieci testowany jest paczkami, zawierającymi po 1000 elementów. Wynikowa tablica do sprawdzania pobierana jest do zmiennej TT.

Linie skryptu poniżej prezentują ustawienia iteracji, błędu oraz inicjalizację sieci

17 ilosc=(ceil(length(Pnew)/dane)*przesk) 18 zmiana=((start-do_err)/ilosc); 19 [w1,b1,w2,b2,w3,b3]=initff(Pnew,S1,'tansig',S2,'tansig',T,'purelin');

Linia 17- ilość wykonania najbardziej zewnętrznej pętli for. Jest to liczba iteracji w algorytmie. Funkcja ceil służy do zaokrąglania.

Linia 18- zmiana opisuje co ile będzie się zmieniał err_goal

Linia 19 - funkcja initff służy do inicjalizacji sieci, sieć zbudowana jest z 3 warstw, w1-w3 odpowiadają warstwom, b1-b3-odpowiadają biasom poszczególnych warstw, funkcja tansig- to typ funkcji rysującej wykresy. Funkcja initff oczekuje zbioru uczącego i funkcji przejścia.

Poniższy fragment służy do losowania wierszy, zerowania oraz utworzenia macierzy danych

20 ind=ceil(rand(1,dane)*length(Pnew)); 21 Pm=zeros(wiersze,dane); 22 Tm=zeros(1,dane); 23 for i=1:dane, 24 Pm(:,i)=Pnew(:,ind(i)); 25 Tm(:,i)=T(:,ind(i)); 26 end 27 for g=1:1000, 28 for z=1:10, 29 if max(Pm(z,:))==min(Pm(z,:)) 30 ind=ceil(rand(1,dane)*length(Pnew)); 31 Pm=zeros(wiersze,dane); 32 Tm=zeros(1,dane); 33 for i=1:dane, 34 Pm(:,i)=Pnew(:,ind(i)); 35 Tm(:,i)=T(:,ind(i)); 36 end 37 z=1; 38 end 39 end 40 end

Linia 20 - losowanie wierszy z pliku z danymi realizowane jest za pomocą funkcji rand, wynik jest zaokrąglany przez funkcję ceil. Losowanie odbywa się od 0 do 1 i mnożone jest przez długość wektora P, z następnie zaokrąglane.

Linia 21 - inicjalizacja macierzy Pm zerami

Linia 22- inicjalizacja macierzy Tm zerami

Linia 23-26 - pętla wstawiająca dane do macierzy Pm i Tm

Linia 27 - pętla sprawdzająca czy w kolumnie są różne cechy

Linia 28 - sprawdza poszczególne kolumny (od 1 do ilości kolumn)

Linia 29 - sprawdza czy max=min, jeśli tak to występuje ta sama cecha i losowanie odbywa się ponownie

Linia 30 - 40 -ponowne losowanie, zerowanie macierzy i przypisywanie wartości do odpowiednich macierzy

Poniższy kod wypisuje zmienne

41 y 42 ilosc 43 zmiana 44 disp_freq=500; 45 max_epoch=10000; 46 if err_goal>do_err 47 err_goal=err_goal-zmiana; 48 else err_goal=do_err; 49 end 50 lr=0.01; 51 err_goal

- wypisanie obecnego numeru iteracji

- wypisanie ilości wszystkich przejść

- wypisanie zmiany err_goal

- częstotliwość wyświetlania wykresu

- maksymalna liczba kroków uczenia

- warunek zmiany błędu err_goal

- zmiana err_goal o wartość znajdującą się pod zmienną zmiana, zmienia błąd startowy, aż do błędu końcowego

- błąd uczenia

52 tp=[disp_freq,max_epoch,err_goal,lr]; 53 54 [w1,b1,w2,b2,w3,b3,TE,TR]= 55 55trainbpa(w1,b1,'tansig',w2,b2,'tansig',w3,b3,'purelin',Pm,Tm,tp); 56 57 plot(TR) 58 plot(ne) 59 end 60 61 A3=simuff(do_spr,w1,b1,'tansig',w2,b2,'tansig',w3,b3,'purelin'); 62 63 kd=(1-( (sum( abs(TT-A3) >0.5))/length(do_spr) ) )*100

Linia 52 - tp jest współczynnikiem redukcji prędkości uczenia zawarte w nawiasach zmienne to częstotliwość wyświetlania, maksymalna liczba kroków uczenia, błąd err_goal oraz błąd uczenia

Linia 54 - 55- funkcja trainbpa zwraca wyuczone współczynniki wagowe.

Linia 57-58 - funkcje rysujące wykresy

Linia 61 - funkcja simuff wyznacza wyjście sieci. Wyjście dąży do wyjścia pożądanego.

Linia 63 - obliczanie ilości poprawnie nauczonych danych. Ilość ta wyrażana jest w procentach

Funkcja trainbpa wykorzystana w realizacji projektu służy do treningu sieci jednokierunkowej (do 3 warstw) ze wsteczną propagacją błędu i adaptacyjnym współczynnikiem uczenia.

Wywołanie:

[W, B, TE, TR] = trainbpa (W, B, 'F', P, T, TP)

Argumenty:

W - macierz współczynników wagowych i-tej warstwy (wymiar Si*R, Si - ilość neuronów w i-tej warstwie, R - ilość wejść warstwy)
B - wektor współczynników progowych i-tej warstw (wymiar Si*l)
F - funkcja aktywacji i-tej warstwy (np. 'logsig')
P - macierz wektorów wejściowych (wymiar R*Q, R - liczba wejść sieci, Q - ilość wektorów)
T - macierz zadanych wektorów wyjsciowych (wymiar S*Q, S - liczba wyjsc sieci)
TP - wektor parametrów:
TP(1) - częstotliwość aktualizacji wykresu błędu sieci (w cyklach, domyślnie = 25)
TP(2) - maksymalna liczba cykli treningowych (domyślnie 100)
TP(3) - graniczny błąd średniokwadratowy) sieci (domyślnie = 0.02)
TP(4) - współczynnik prędkości uczenia (domyślnie = 0.01)

Wielkości zwracane:
W - macierz nowych współczynników wagowych i-tej warstwy (wymiar Si * R)
B - wektor nowych współczynników progowych warstwy (wymiar Si*l)
TE - liczba przebytych cykli treningowych
TR - średniokwadratowy bład sieci

TP(5) - współczynnik wzrostu prędkości uczenia (domyślnie 1.05)
TP(6) - współczynnik redukcji prędkości uczenia (domyślnie = 0.7)
TP(7) - maksymalna wartość współczynnika błędu (domyślnie = 1.04)

Eksperymenty

Numer testu	Rozmiar wejścia	Neurony w warstwie S1	Neurony w warstwie S2	Procent nauczonych danych (kd)	Spostrzeżenia, Uwagi
1	100	5	5	37	Dość niski wynik, wymagane jest podniesienie liczby neuronów
2	100	10	5	55	Zwiększenie liczby neuronów poprawiło wynik
3	100	10	10	37	Ustalenie równej liczby neuronów w obu warstwach, Obniżenie wyniku
4	100	5	10	52	Spadek wyniku po podniesieniu liczby neuronów po zamianie ilości w warstwach w stosunku do testu 2
5	100	10	15	40	Podniesienie liczby neuronów w warstwie 2 , wzrost wyniku
6	100	10	20	35	Wynik spadł
7	100	15	20	37	Wynik podniósł się po zwiększeniu liczby neuronów w warstwie pierwszej
8	100	20	20	40	Zwiększenie neuronów w warstwie 1 poprawiło wynik
9	100	20	25	24	Spadek procentu nauczonych danych po podniesieniu liczby neuronów
10	100	20	30	39	Podniesienie liczby neuronów poprawiło wynik
11	100	20	15	40	Wynik utrzymuje się
12	100	20	10	53	Sieć uzyskała dość dobry rezultat
13	1000	10	10	38	Początkowy wynik dla paczki 1000 Przy równej liczbie neuronów w warstwach
14	1000	20	10	50	Podniesienie liczby neuronów poprawiło wynik
15	1000	20	20	63,9	Podniesienie liczby neuronów poprawiło wynik
16	1000	30	20	43
17	1000	40	30	34	Pogorszenie wyniku, liczba neuronów jest zbyt duża
18	5000	10	10	59	Poprawa wyniku przy większej paczce
19	5000	20	10	60,9	Ustawienie dwukrotnej liczby neuronów na warstwie pierwszej w stosunku do warstwy drugiej
20	5000	20	20	65,9	Poprawienie wyniku wraz z podwyższeniem liczby neuronów, neurony rozłożone po równo w obu warstwach
21	5000	20	30	71	Poprawienie wyniku wraz z podwyższeniem liczby neuronów
22	5000	30	30	67	Wynik uległ spadkowi
23	10000	10	10	67	Dobry wynik uzyskany przy równej liczbie neuronów w obu warstwach
24	10000	20	10	78	Podniesienie liczby neuronów w pierwszej warstwie skutkuje lepszym wynikiem
25	10000	20	20	100	Uzyskano 100% zgodność na poziomie 40 neuronów

Sieć uczona była za pomocą paczek 100, 1000, 5000 oraz 10000 elementowych. Dobieranie współczynników odpowiednio wpływało na wynik. Strategia uczenia jaką przyjąłem można nazwać „od szczegółu do ogółu”. Na początku podawałem sieci rozmiarowo małe paczki dążąc do jak najlepszego ich wyuczenia, po czym podając coraz większe paczki uogólniałem nabyte przez sieć doświadczenia na większą liczbę rozdań.

Rys 1 Sieć podczas uczenia się

Rys 2 Wykres współczynnika uczenia

Rys 3 Uczenie się sieci

Poniżej zamieściłem wykresy reprezentujące zmianę procentu nauczonych danych (kd) od ilości danych w paczce oraz ilości neuronów w poszczególnych warstwach. Wykresy te obrazują wpływ poszczególnych ustawień na wynik końcowy.

Rys 4 Zależność nauczonego procentu danych od ilości danych w paczce

Rys 5 Zależność nauczonego procentu danych liczby neuronów dla całości

Rys 6 Zależność nauczonego procentu danych liczby neuronów dla całości

Poniżej prezentuję szczegółowe odsetki nauczonych danych dla poszczególnych paczek.

Rys 7 Zależność nauczonego procentu danych liczby neuronów - paczka 100

Rys 8 Zależność nauczonego procentu danych liczby neuronów - paczka 1000

Rys 9 Zależność nauczonego procentu danych liczby neuronów - paczka 5000

Rys 10 Zależność nauczonego procentu danych liczby neuronów - paczka 10000

Podsumowanie

Po wykonaniu szeregu eksperymentów dla różnych wartości wejścia mogę stwierdzić że sieć lepiej uczy się dla większych ilości danych. Przy 10000 możliwe było uzyskanie stuprocentowego dopasowania. Może to być spowodowane tym że danych których ma się nauczyć sieć jest milion, podając jej na wejście większy zbiór jest ona w stanie zgromadzić więcej wiedzy na temat poszczególnych rozdań, co powoduje, ze po sprawdzeniu stopnia nauczenia się sieci możemy uzyskać lepsze wyniki.

Ilość neuronów także odgrywa bardzo ważną rolę. Można dostrzec pewne prawidłowości w działaniu sieci. Jeżeli sieć ma za mało neuronów ma uczy się źle, generując duże błędy średniokwadratowe. Umiejętne zwiększanie liczby neuronów w poszczególnych warstwach wpływa na poprawę wyniku końcowego. Udało mi się dostrzec, że ustawienie neuronów po równo w obu warstwach dość dobrze wpływa na sieć, gdyż wyniki uzyskane w ten sposób były zadowalające, w ten sposób uzyskałem także wynik stuprocentowy. Sieć lepiej się uczy realizując postawione przed nią zadanie. Jednak gdy liczba neuronów dla danej paczki jest zbyt duża dochodzi do pogorszenia parametrów procesu uczenia, wynik końcowy spada.

Zastosowany w projekcie algorytm trainbpa nie jest zbyt wydajny jeśli chodzi o proces uczenia. Sieć uczy się dość wolno. Potrzeba jej wielu eksperymentów. Znając podstawy programowania w środowisku Matlab możemy zasymulować wiele skomplikowanych sytuacji. Mój skrypt jest krótki, zawiera kilkadziesiąt linii kodu. Zrealizowanie podobnego problemu w jednym z popularnych języków programowania takich jak C lub C++ zajęłoby o wiele więcej linii i wymagałoby znacznej wiedzy programisty oraz zajęłoby sporo czasu .

Sieci neuronowe mają zastosowanie w obecnej chwili w wielu dziedzinach życia. Służą do rozpoznawania, przewidywania, planowania. Za ich pomocą można np. przewidzieć ruchy giełdowe, rozpoznawać kody z obrazka, bądź tworze ludzi. Dzięki sieciom neuronowym możemy przeanalizować dane, które nie mają na pierwszy rzut oka nic wspólnego ze sobą, co pomaga w dostrzeżeniu pewnych prawidłowości.

14

---