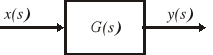2. OPIS MATEMATYCZNY CZŁONÓW I UKŁADÓW LINIOWYCH AUTOMATYKI
Pierwszym etapem syntezy układów automatycznej regulacji (UAR) jest ułożenie równań różniczkowych dla elementów wpływających funkcjonalnie na proces regulacji. Należą do nich: elementy wykonawcze, czujniki pomiarowe uchybu regulacji, bloki porównujące, wzmacniające itd. Mogą to być elementy elektryczne, mechaniczne, pneumatyczne lub hydrauliczne. Często bywają to elementy mieszane, np. pneumatyczno-elektryczne. Metodyka układania równań różniczkowych (tworzenia modeli fizycznych) ma charakter ogólny, niezależny od rodzaju elementu. Obowiązują przy tym pewne zasady jak i metody tworzenia tych modeli. Zostaną one szczegółowo omówione w tym wykładzie.
2.1. Zasady ogólne
Analiza i synteza układów automatycznej regulacji wymaga znajomości właściwości statycznych i dynamicznych elementów wchodzących w skład tych układów. Właściwości te zawarte są w ich opisie matematycznym.
Opis matematyczny ciągłego elementu lub układu automatyki o jednym wejściu i jednym
wyjściu składa się w ogólnym przypadku z dwóch części:
równania lub wykresu charakterystyki statycznej, określającego zależność sygnału
wyjściowego od wejściowego w stanach ustalonych,
2) równania różniczkowego lub operatorowego, opisującego właściwości statyczne i dynamiczne w otoczeniu wybranego na charakterystyce statycznej punktu pracy.
Jeżeli charakterystyka statyczna jest prostoliniowa, jako kompletny opis właściwości elementu wystarczy podać równanie różniczkowe lub operatorowe, które opisuje wówczas właściwości statyczne i dynamiczne w całym zakresie pracy, a nie tylko w otoczeniu wybranego punktu.
Jeżeli charakterystyka statyczna jest krzywoliniowa, niezbędna jest znajomość obu części opisu, gdyż współczynniki równania różniczkowego są wówczas zmienne wzdłuż charakterystyki statycznej. Linearyzacja polega na zastąpieniu krzywoliniowego odcinka charakterystyki odcinkiem prostoliniowym, stycznym do rzeczywistej charakterystyki statycznej w wybranym punkcie. W przybliżeniu można wtedy traktować charakterystykę statyczną jako prostoliniową, a współczynniki równania różniczkowego jako stałe, w otoczeniu danego punktu.
Omawiane dalej metody opisu matematycznego elementów liniowych można więc rozciągnąć również na elementy linearyzowane.
Modelem matematycznym ciągłego jednowymiarowego elementu sterowania o stałych skupionych jest opisujące go równanie różniczkowe zwyczajne
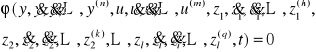
(2.1)
Równanie to opisuje niestacjonarny, jednowymiarowy element nieliniowy. Gdy element jest stacjonarny to w równaniu (2.1) nie występuje bezpośrednia zależność od czasu. Gdy element jest liniowy względem sygnału wejściowego i względem zakłóceń z1, z2, ... , zl, równanie (2.1) jest liniową kombinacją sygnałów i ich pochodnych. Dla obiektu niestacjonarnego mamy wtedy
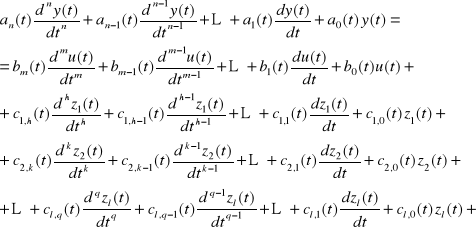
(2.2)
Przy czym: ![]()
![]()
są współczynnikami zależnymi od parametrów elementu.
Przez h, k, ..., q oznaczono dla sygnałów z1, z2, ..., zl najwyższy rząd pochodnych tych sygnałów występujących w równaniu (2.1).
W ciągłych stacjonarnych układach liniowych współczynniki przy poszczególnych wyrazach równania (2.2) są stałe (parametry układu nie ulegają zmianie w czasie):
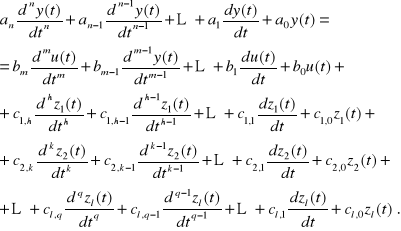
(2.3)
W dalszym ciągu naszych rozważań będziemy zajmować się elementami jednowymiarowymi liniowymi stacjonarnymi o stałych skupionych - opisanych równaniami typu (2.3). Zależnie od warunków pracy takich elementów należy wyróżnić cztery następujące przypadki:
Na element działa zarówno sygnał sterujący, jak i sygnały zakłócające. Dynamikę elementu opisuje równanie (2.3).
Na element działa tylko sygnał sterujący, a wszystkie zakłócenia i ich pochodne są równe tożsamościowo zero. W takim przypadku dynamika elementu jest opisana równaniem
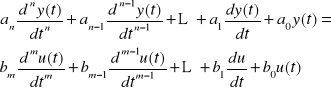
(2.4)
Na element nie działa sygnał sterujący (sygnał ten i jego pochodne są równe zero). Dynamikę elementu, na który działają tylko zakłócenia opisuje równanie

(2.5)
Na element nie działają żadne sygnały zewnętrzne - tzn., że sygnał sterujący i jego wszystkie pochodne oraz sygnały zakłócające i ich wszystkie pochodne są równe tożsamościowo zero. Równanie opisujące dynamikę elementu upraszcza się do postaci
![]()
(2.6)
Jest to równanie elementu (układu) w stanie swobodnym. Przez analogię do zjawisk w układach mechanicznych jest także nazywane równaniem ruchu swobodnego lub równaniem drgań własnych. Charakteryzuje ono zachowanie się obiektu po odjęciu wszelkich sygnałów zewnętrznych i ma istotne znaczenie przy badaniu właściwości obiektów stacjonarnych, ciągłych, liniowych o stałych skupionych.
Dalsze rozważania prowadzić będziemy w oparciu o ogólną postać równania różniczkowego liniowego o stałych współczynnikach opisującego właściwości ciągłego elementu lub jednowymiarowego układu liniowego o parametrach stałych czyli stacjonarnego (rys. 1.2a):
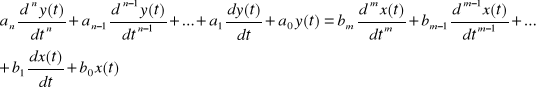
(2.7)
przy czym n ![]()
m dla wszystkich elementów i układów rzeczywistych. W równaniu tym przyjęto oznaczenia:
y - wielkość wyjściowa,
x - wielkość wejściowa (sygnał sterujący, zakłócenie),
t - czas,
ak, bl - współczynniki stałe (k = 0, 1, ... , n; l = 0, 1, ... , m).
Z równania (2.7) wynika charakterystyka statyczna (w stanie ustalonym wszystkie pochodne są równe zero)
![]()
(2.8)
przy czym dla elementów linearyzowanych jest to równanie stycznej do charakterystyki rzeczywistej, a jako początek układu współrzędnych (x = 0, y = 0) należy wówczas rozumieć punkt styczności, tzn. punkt pracy, wokół którego przeprowadzono linearyzację.
2. 2. Opis właściwości dynamicznych liniowych UAR
Przez układy liniowe rozumiemy takie układy, do których można zastosować zasadę superpozycji. Omawiać będziemy podstawowe równania obowiązujące dla liniowego zakresu pracy układów najczęściej spotykanych w urządzeniach automatyki, a więc układów: mechanicznych, elektrycznych, pneumatycznych i hydraulicznych.
Wyróżnimy trzy rodzaje elementów:
A. Elementy powodujące straty energii rozpraszanej na energię cieplną (tarcie, oporność czynna w układach elektrycznych, opór przepływu gazów i cieczy).
B. Elementy magazynujące energię w postaci kinetycznej (masa, indukcyjność w układach elektrycznych, bezwładność cieczy i gazów).
C. Elementy magazynujące energię w postaci potencjalnej (sprężystość, pojemność w układach elektrycznych, ściśliwość gazów, a w układach hydraulicznych napełnianie zbiorników).
Założenia upraszczające
Ograniczymy się tylko do liniowego zakresu pracy. Przyjmiemy więc, że np. w układach elektrycznych wartości oporności, indukcyjności i pojemności są stałe, niezależne od prądu i napięcia.
W przypadku układów mechanicznych założymy, że składają się z ciał idealnie sztywnych i sprężyn idealnych o znikomo małej masie, i że siła tarcia jest proporcjonalna do prędkości w pierwszej potędze (tarcie lepkie).
Dla układów pneumatycznych przyjmiemy, że spadek ciśnienia na oporach przepływu jest proporcjonalny do przepływu, czyli że wartość oporu przepływu jest stała, niezależna od natężenia przepływu i ciśnienia, gaz zaś jest doskonale sprężysty, o stałej wartości współczynnika sprężystości.
Natomiast w układach hydraulicznych założymy, że ciecze są nieściśliwe, a spadek ciśnienia na oporach przepływu jest proporcjonalny do wielkości tego przepływu, czyli że opory przepływu mają wartości stałe, niezależne od natężenia przepływu i ciśnienia.
Elementy wymienione w punkcie A powodują przy przenoszeniu sygnałów straty zawartej w nich energii. Moc idąca na straty Ps określona jest wzorami:
w układach elektrycznych
Ps = i2 R (2.9)
gdzie: i - natężenie prądu elektrycznego [A], R - rezystancja [Ω],
w układach mechanicznych o ruchu postępowym
Ps = v2 Rm (2.10)
gdzie: v - prędkość ruchu postępowego [m/s], Rm - opór tarcia [kg/s],
w układach mechanicznych o ruchu obrotowym
Ps = ![]()
2 Rr (2.11)
gdzie: ω - prędkość kątowa [rad/s], Rr - opór tarcia w ruchu obrotowym [kg m2/s],
w układach pneumatycznych i hydraulicznych
![]()
(2.12)
gdzie: ip - natężenie przepływu [m3/s], Rp - opór przepływu [kg/m4s],
Elementy wymienione w punkcie B magazynują energię w postaci energii kinetycznej Ek, która określona jest wzorami:
w układach elektrycznych
![]()
(2.13)
gdzie: L - indukcyjność [H],
w układach mechanicznych o ruchu postępowym
![]()
(2.14)
gdzie: m - masa [kg],
w układach mechanicznych o ruchu obrotowym
![]()
(2.15)
gdzie: J - moment bezwładności [kg m2],
w układach pneumatycznych i hydraulicznych
![]()
(2.16)
gdzie: mp - masa płynu przepływającego przez jednostkę długości w jednostce czasu [kg m-1 s-1].
Elementy wymienione w punkcie C magazynują energię w postaci potencjalnej. Zmagazynowana w nich energia określana jest wzorami:
w układach elektrycznych
![]()
(2.17)
przy czym: q - ładunek elektryczny [C], C - pojemność [F],
w układach mechanicznych o ruchu postępowym
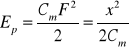
(2.18)
gdzie: F - siła [N], Cm - współczynnik sztywności sprężyny (na rozciąganie) [m/N], 1/Cm = Cs - współczynnik sprężystości, x - przemieszczenie [m],
w układach mechanicznych o ruchu obrotowym
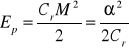
(2.19)
gdzie: M - moment obrotowy [Nm], Cr - współczynnik sztywności sprężyny (na skręcanie) [rad/Nm], α - kąt [rad ],
w układach pneumatycznych
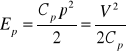
(2.20)
gdzie: p - ciśnienie [N/m2 = Pa], Cp - współczynnik sprężystości gazu [m3/Pa], V - objętość [m3],
w układach hydraulicznych
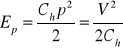
. (2.21)
gdzie: Ch - współczynnik sprężystości cieczy [m3/Pa].
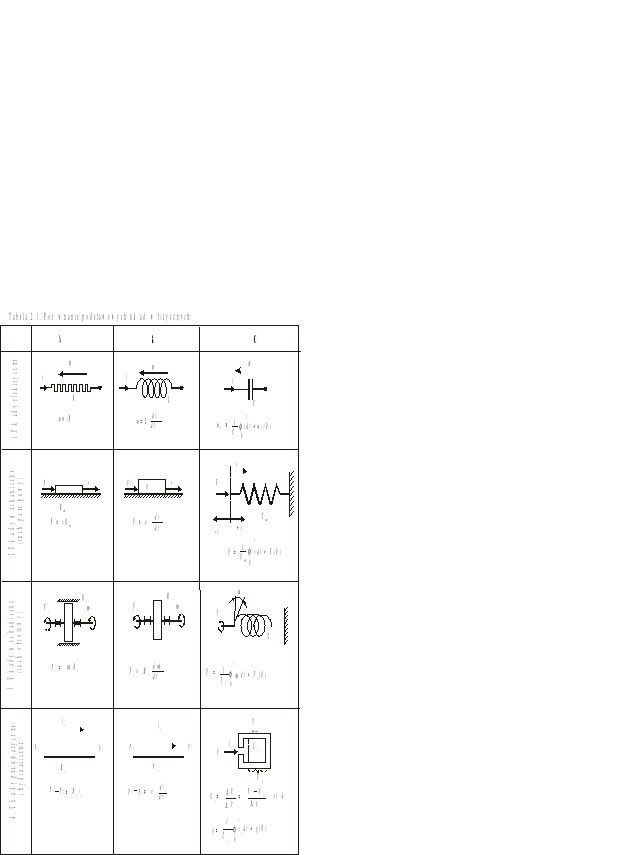
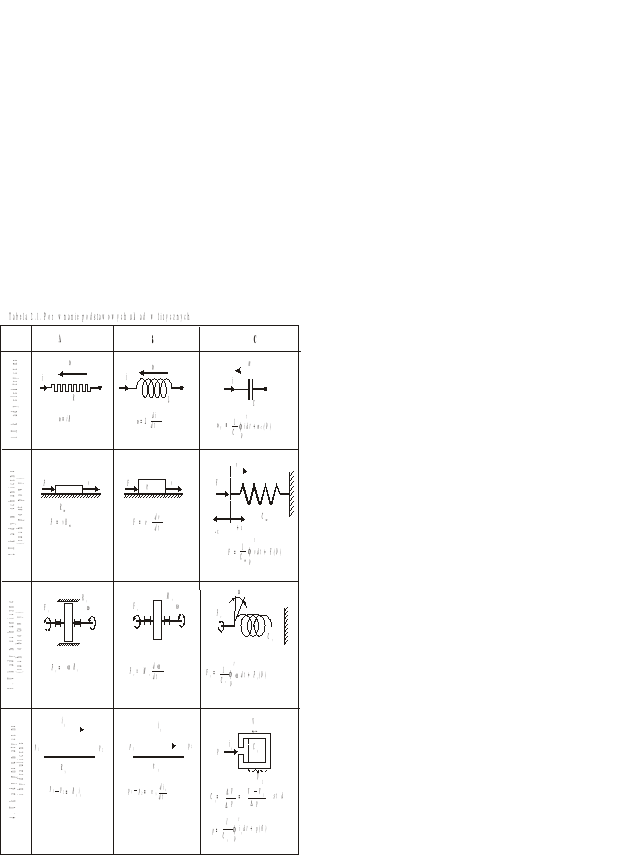
Istnieje pełna analogia pomiędzy układami elektrycznymi, mechanicznymi i płynowymi. Zwięźle pokazuje tą analogię tabela 2.1. Oto krótki komentarz do zawartych w niej treści.
W kolumnie A tabeli 2.1 zgrupowane są elementy powodujące straty energii.
Są to:
Rezystancję R (poz. 1-A) wyznaczamy z prawa Ohma
![]()
(2.22)
gdzie: u - napięcie elektryczne w [V], i - prąd elektryczny w [A].
Współczynnik oporu Rm w układach mechanicznych o ruchu postępowym (poz. 2-A) wyrażony wzorem
![]()
(2.23)
gdzie: F - siła [N], v - prędkość ruchu postępowego [m/s].
Współczynnik oporu Rr w układach mechanicznych o ruchu obrotowym (poz. 3-A) dany wzorem
![]()
(2.24)
gdzie: M - moment obrotowy [Nm], ω - prędkość kątowa [rad/s].
Opór przepływu Rp w układach pneumatycznych i hydraulicznych (po. 4-A) przedstawiony wzorem
![]()
(2.25)
przy czym p1, p2 - ciśnienie na wejściu i wyjściu przewodu [N/m2], ip - przepływ [m3/s].
W kolumnie B zgrupowano elementy magazynujące energię w postaci kinetycznej.
Są to:
Cewka elektryczna o indukcyjności L (poz. 1-B) dla której możemy zapisać
![]()
(2.26)
Dla ciała sztywnego o masie m (układ mechaniczny o ruchu postępowym, poz. 2-B) możemy napisać
![]()
(2.27)
a dla ciała sztywnego o momencie bezwładności J (układ mechaniczny o ruchu obrotowym, poz. 3-B)
![]()
(2.28)
Bezwładność mp gazów i cieczy (poz. 4-B) wyrażana jest zależnością
![]()
(2.29)
gdzie: p1, p2 - ciśnienie na wejściu i wyjściu przewodu, ip - przepływ, m - całkowita masa substancji (gaz, ciecz) znajdującej się w danym przewodzie, A - powierzchnia przekroju przewodu [m2], ![]()
.
W kolumnie C zgromadzone są elementy magazynujące energię w postaci potencjalnej. Należą do nich:
Kondensator o pojemności C (poz. 1-C) i napięciu
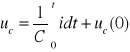
(2.30)
gdzie: uc - początkowe napięcie na kondensatorze [V].
Dla elementu sprężystego o współczynniku Cm w układach mechanicznych o ruchu postępowym (poz. 2-C) możemy napisać
![]()
a stąd
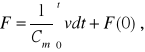
(2.31)
gdzie: Δx - przesunięcie, jakiego dozna dana sprężyna pod wpływem przyrostu siły Δf, f(0) - początkowa wartość siły w chwili t = 0.
Element sprężysty o współczynniku Cr w układach mechanicznych o ruchu obrotowym (poz. 3-C) zdefiniujemy jako
![]()
a stąd
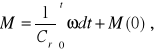
(2.32)
przy czym: Δα - kąt skręcenia, jakiego dozna sprężyna pod wpływem przyrostu momentu ΔM, M(0) - początkowa wartość momentu skręcającego.
Współczynnik sprężystości Cp gazu w komorze pneumatycznej (poz. 4-C). Jeżeli pod wpływem zmiany ciśnienia o Δp = p - p(0) gaz w komorze zajmujący poprzednio przy ciśnieniu p(0) objętość V zostanie ściśnięty do objętości V1, to
![]()
a stąd
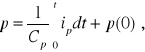
(2.33)
przy czym: ip - przepływ, p(0) - ciśnienie w chwili początkowej.
Właściwości dynamiczne opisanych układów najogólniej ujmuje równanie Lagrange'a w postaci
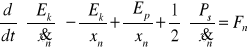
(2.34)
przy czym Ek, Ep - odpowiednio energia kinetyczna i potencjalna, Ps - moc sił niezachowawczych (sił oporu proporcjonalnych do prędkości), xn - współrzędna uogólniona (odpowiednio: x i α - w układach mechanicznych, q - w układach elektrycznych, V - w układach pneumatycznych i hydraulicznych), ![]()
- pochodna zmiennej xn względem czasu, Fn - pobudzenie związane ze współrzędną uogólnioną xn.
Zastosowanie równań Lagrange'a w obliczeniach praktycznych może czasami sprawiać duże trudności, tak że automatycy częściej korzystają z praw fizycznych dotyczących rozważanych zagadnień, np.: praw Kirchhoffa, Newtona, d'Alemberta czy też praw Bernoulliego, Poissona-Stockesa związanych z przepływem gazu i cieczy.
Równania Lagrange'a mają jednak podstawowe znaczenie pojęciowe, wskazując jedność i analogie między różnymi układami.
Poniżej podane zostaną przykłady układania równań różniczkowych różnych elementów z wykorzystaniem zarówno równań Lagrange'a jak i praw fizyki.
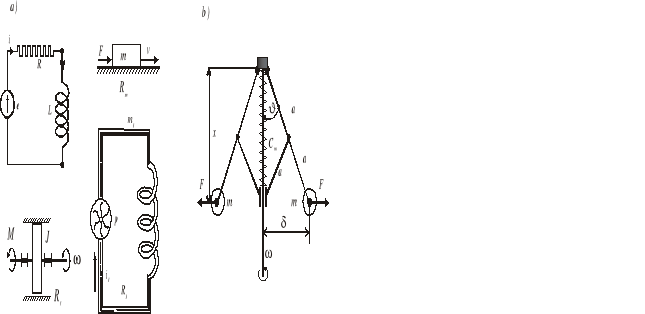
Przykład 2.1. Zastosujemy równanie Lagrange'a dla określenia właściwości układów dynamicznych przedstawionych na rys. 2.1a. Są to układy o jednym stopniu swobody. Mają zatem po jednej współrzędnej uogólnionej.
Układ elektryczny
![]()
przy czym q - ładunek elektryczny.
Układ mechaniczny
ruch postępowy
![]()
ruch obrotowy
![]()
Układ hydrauliczny
![]()
W rozpatrywanych przypadkach mamy więc odpowiednio następujące wartości członów równania (2.34):
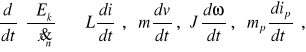
![]()
![]()
![]()
- nie jest reprezentowane, gdyż brak jest układów magazynujących energię w postaci potencjalnej,
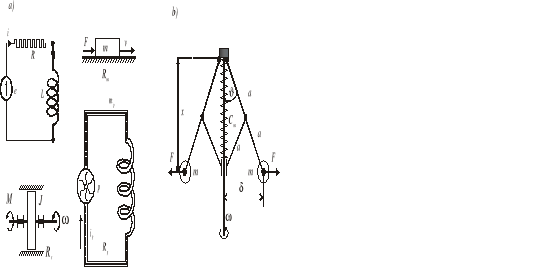
![]()
Rys. 2.1. Przykłady elementów i procesów mających zastosowanie w układach automatycznego sterowania
Na podstawie równania (2.29) mamy więc wprost:
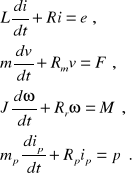
(2.35)
Przykład 2.2. Na rys. 2.1b przedstawiony jest schemat regulatora Watta. Jest to również układ o jednym stopniu swobody. Jako współrzędną uogólnioną przyjmiemy kąt ϑ.
Energia kinetyczna układu jest sumą energii kinetycznej ruchu obrotowego i liniowego układu, odpowiednio równych:
energia kinetyczna ruchu obrotowego
![]()
energia kinetyczna ruchu postępowego
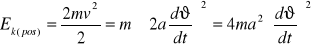
.
Całkowita energia kinetyczna układu
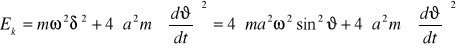
, (2.36)
gdzie wykorzystaliśmy fakt, że ![]()
.
Energia potencjalna jest sumą energii potencjalnej dwóch mas i sprężyny:
![]()
(2.37)
a moc tracona na tarcie:
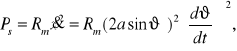
(2.38)
gdzie: ω - prędkość kątowa, m - masa jednej kuli, g - przyspieszenie grawitacyjne, Cm - współczynnik sprężystości sprężyny, Rm - współczynnik oporu, x* - długość nie ściśniętej sprężyny. Pozostałe oznaczenia przedstawiono na rys. 2.1b.
Wymuszenie fn związane ze współrzędną ϑ jest równe zero. Mamy więc:
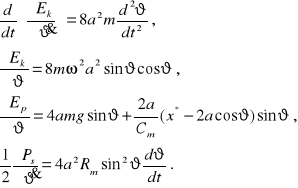
(2.39)
Wstawiając równania (2.39) do (2.34) otrzymujemy równanie opisujące regulator Watta w postaci:
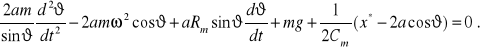
(2.40)
Jest to równanie nieliniowe wiążące kąt ϑ z wymuszeniem ω .
Ponieważ wielkością wyjściową omawianego elementu jest przesunięcie x, więc bardziej interesujące jest równanie różniczkowe wiążące wielkości x i ω. Łatwo je otrzymamy uwzględniając, że:
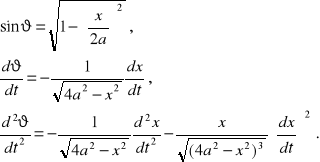
(2.41)
Po przekształceniach otrzymujemy następujące równanie różniczkowe:
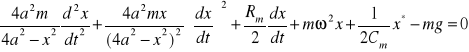
(2.42)
Równanie to jest również równaniem nieliniowym.
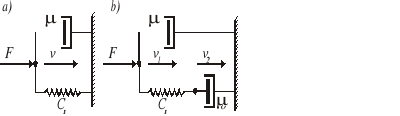
Przykład 2.3. Wyznaczyć równania różniczkowe układów mechanicznych przedstawionych schematycznie na rys. 2.2. Wielkością wejściową jest siła F, wielkością wyjściową siła reakcji sprężyny.
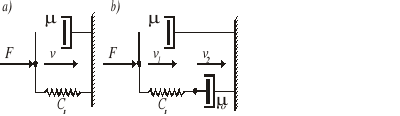
Rys. 2.2. Schematy układów do przykładu 2.3; Cs - współczynnik sprężystości sprężyny, μ, μo - współczynniki tarcia lepkiego
Rozwiązanie
Równania dynamiki wypisujemy korzystając z zasady d'Alemberta. Zgodnie z tą zasadą
siła reakcji tłumika (rys. 2.3) o współczynniku tarcia lepkiego μ jest równa:
![]()
(2.43)
gdzie:v1( t) - prędkość tego końca tłumika, na który oddziałuje wymuszenie,

v2( t) - prędkość drugiego końca tłumika.
Podobnie siła reakcji sprężyny (rys. 2.4) o współczynniku sprężystości Cs jest równa:
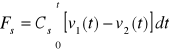
(2.44)
lub, jeśli brać pod uwagę przesunięcia x(t) od położeń początkowych (zerowych) x10 i x20:
![]()
(2.45)
Siła reakcji punktu materialnego o masie m jest równa:
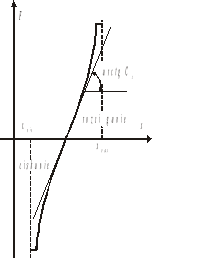
![]()
2.46)
gdzie v(t) - prędkość z jaką układ się porusza.
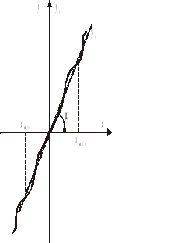
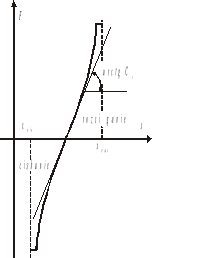
Rys. 2.5. Charakterystyka statyczna sprężyny
Charakterystyka statyczna sprężyny teoretycznie jest nieliniowa. Można ją linearyzować.
Linearyzacja polega tutaj na uwzględnieniu tylko tarcia lepkiego a pominięciu tarcia suchego oraz założeniu, że styczna do charakterystyki statycznej sprężyny (rys. 2.5) ma w punkcie pracy (x0 = x1 - x2, F = 0) nachylenie Cs, zaś odchylenia od punktu pracy są niewielkie.
Wyjście poza obszar (xmin, xmax) oznacza trwałe odkształcenie sprężyny.
Jeżeli siłę reakcji sprężyny określić przybliżeniem sześciennym ![]()
, to linearyzacja w dowolnym punkcie pracy x0 daje zależność zlinearyzowaną (patrz rozdz. 2.3)
![]()
Rozpatrując zatem układ mechaniczny musimy wyznaczyć wszystkie punkty, w których prędkości są równe i założywszy ich kierunki wypisać równania.
W układzie pokazanym na rys. 2.2a jest tylko jedna prędkość różna od zera, gdyż drugie końce sprężyny i tłumika są zamocowane. Układ będzie opisany więc tylko jednym równaniem:
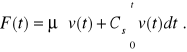
(2.47)
W układzie pokazanym na rys. 2.3b są dwie prędkości v1 i v2. Równania różniczkowe układu zlinearyzowanego przyjmą postać:
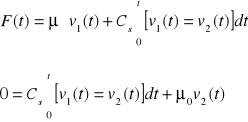
(2.48)
We wzorach (1.38) - (1.41) można dostrzec pełną analogię układów mechanicznych i elektrycznych. Jeśli przyjąć, że sile F odpowiada siła elektromotoryczna E, to mamy przypadek analogii napięciowej.
Tablica 2.2
ruch |
analogia |
obrotowy |
liniowy |
napięciowa |
prądowa |
M ω μ 1/Cr y |
F v μ 1/Cm m |
E i R C L |
I u 1/R L C |
Równie dobrze można stosować analogię prądową (patrz Tab. 2.2). Stosując metodę prądów oczkowych w elektrotechnice, wypisujemy układ równań dla prądów w poszczególnych oczkach. Podobnie dla układów mechanicznych konstruujemy układ równań dla poszczególnych prędkości w układzie.
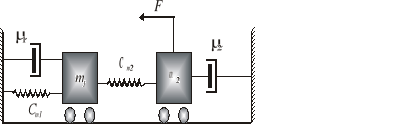
Przykład 2.4. Opisać równaniami różniczkowymi układ mechaniczny przedstawiony na rys. 2.6.
Rozwiązanie
W układzie można wyróżnić dwie prędkości różne od zera: prędkość v1(t) masy m1 oraz prędkość v2(t) masy m2. Wymuszenie F jest równoważone przez siły reakcji elementów m2, Cm2, μ2 zgodnie z równaniem:
![]()
(2.49)
Prędkość v2 nie jest wymuszona bezpośrednio przez żadną siłę, odpowiednie równanie ma postać:
![]()
(2.50)
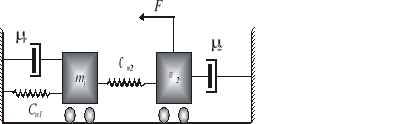
Rys. 2.6. Schemat układu mechanicznego do przykładu 2.4.
2.3. Linearyzacja charakterystyk statycznych i równań różniczkowych
Często spotyka się elementy, które posiadają nieliniową tylko charakterystykę statyczną. Załóżmy, że w pewnym przedziale zmienności sygnału wejściowego xmin< x <xmax nieliniowa charakterystyka statyczna może być aproksymowana linią prostą ya (rys. 2.7) i że w czasie pracy elementu, sygnał wielkości wejściowej x zmieniał się będzie w założonym przedziale. Wówczas prosta ya może być uznana za charakterystykę statyczną. Możemy wówczas zapisać w przybliżeniu
![]()
(2.51)
gdzie: k = tg α.
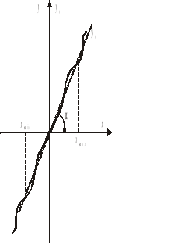
Rys. 2.7. Linearyzacja charakterystyki statycznej metodą uśrednienia
Taką prostą linearyzację - metodę uśrednienia - stosuje się w inżynierskiej praktyce, kiedy wystarczająco gładka charakterystyka nie może być aproksymowana funkcją analityczną.
Częściej stosuje się jednak metodę małych odchyleń, jako narzędzie pozwalające linearyzować zarówno charakterystyki statyczne jak i nieliniowe równania różniczkowe.
Sens tej metody przedstawimy na przykładzie linearyzacji równania
![]()
(2.52)
gdzie: x = x(t) i v = v(t) - wielkości wejściowe (zadane funkcje czasu);
y = y(t) - wielkość wyjściowa (szukana funkcja czasu).
Drugi stopień równania i stosunkowo niewielka ilość argumentów funkcji φ przyjęta została dla zwiększenia czytelności wywodu. Omawiana metoda pozwala na przeprowadzenie linearyzacji równania różniczkowego dowolnego stopnia z nieograniczoną ilością argumentów funkcji φ.
Jeśli funkcja φ posiada pochodne względem wszystkich swoich argumentów to może zostać rozwinięta w szereg Taylora w dowolnie wybranym punkcie pracy zwanym punktem nominalnym. Przy linearyzacji równań opisujących UAR punktem nominalnym powinien być punkt odpowiadający stanowi ustalonemu układu. Załóżmy, że w tym stanie pracy x=x0, v=v0 oraz y=y0 są stałymi wielkościami, a ![]()
.
Wówczas po rozwinięciu funkcji φ w szereg otrzymamy
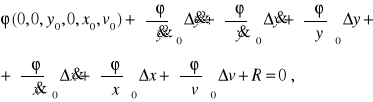
(2.53)
gdzie: ![]()
odchyłki zmiennych od wartości ustalonych;
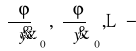
pochodne cząstkowe funkcji φ dla ![]()
R - nieliniowa część rozwinięcia funkcji φ w szereg Taylora.
W stabilnych UAR odchyłki ![]()
z definicji są dostatecznie małe. Dlatego składniki sumy R w równaniu (2.53) zawierające te odchyłki w kwadracie i wyższych potęgach oraz pochodne wyższych rzędów są małe i mogą być pominięte (R ≈ 0). Dodatkowo, należy uwzględnić, że dla stanu ustalonego
![]()
Ostatecznie otrzymamy zlinearyzowaną postać równania (2.52)
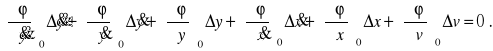
(2.54)
Zmiennymi w tym równaniu są nie x, v i y lecz ich odchyłki od stanu ustalonego. Jednak bardzo często występują zerowe warunki początkowe x0 = v0 = y0 = 0 i dlatego Δx = x, Δv = v, Δy = y a zlinearyzowane równanie jest wówczas równaniem dla zmiennych y, x, v:
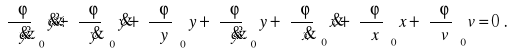
(2.55)
Gdy współczynniki równania (2.54) są uzależnione od czasu to zlinearyzowane równanie jest równaniem niestacjonarnym.
Przyjęte założenie o dostatecznie małych odchyłkach ![]()
jest słuszne wtedy, kiedy zmienne x i v są wielkościami wyjściowymi innych elementów zamkniętego UAR. Jeśli zaś któraś z tych wielkości (lub wszystkie) jest zmienną zewnętrzną (wymuszeniem), to należy sprawdzić, czy uzasadnione jest takie założenie.
Metody małych odchyleń nie możemy stosować, jeśli funkcja φ jest nieciągła lub niejednoznaczna względem dowolnego argumentu.
Przykład 2. 5. Układ jest opisany równaniem różniczkowym
![]()
(2.56)
Należy wyznaczyć równanie różniczkowe zlinearyzowane.
Rozwiązanie. Jest to równanie nieliniowe pierwszego rzędu - nieliniowość spowodowana jest zarówno zależnością współczynnika g od zmiennej y, jak i występowaniem członu ![]()
.
Przekształcając (2.56) do postaci (2.52) mamy
![]()
Aby dokonać rozwinięcia w szereg Taylora, wyznaczamy pochodne funkcji φ w punkcie (x0, y0):
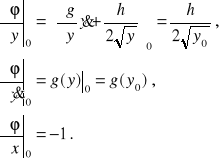
Zlinearyzowane równanie przyjmie postać
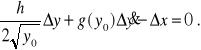
2. 4. Uwagi o równaniach różniczkowych UAR
W liniowym równaniu różniczkowym wielkość wyjściową i jej pochodne przyjęto zapisywać po lewej stronie znaku równości, zaś wielkości wejściowe (zadane funkcje czasu) - po prawej. Dba się również o to, by współczynnik przy wyjściowej wielkości był równy jeden (a0 =1 w równaniu 2.2.). Jeśli równanie nie zawiera wielkości wyjściowej, dąży się aby współczynnik przy najmłodszej pochodnej był równy jedności.
Często dla uproszczenia zapisu korzysta się z symbolu operatora różniczkowania ![]()
, który umownie uważany jest za wielkość algebraiczną. Dodatkowo przyjmuje się, że ![]()
i dopuszcza się różne formy uproszczonego zapisu równania różniczkowego. Na przykład równanie (2.55) możemy zapisać następująco
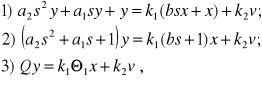
(2.57)
gdzie:
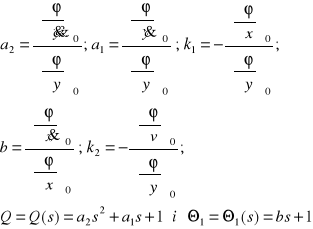
liniowe operatory różniczkowe.
W rzeczywistych UAR na ogół nie występuje potrzeba całkowania równań różniczkowych poszczególnych elementów. Rozpatruje się wspólnie równania wszystkich elementów tworzących dany UAR, czyli układ równań.
Jeśli na układ działa wymuszenie w postaci wartości zadanej w=w(t) i zakłócenia z=z(t) (na przykład według struktury rys. 1.8), to układ równań w przypadku ogólnym będzie miał postać
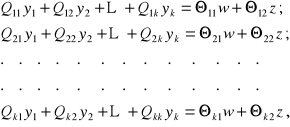
(2.58)
gdzie: Qij=Qij(s); Θi1=Θi1(s) i Θi2=Θi2(s) - liniowe operatory różniczkowe o stałych współczynnikach (niektóre z nich mogą być równe zero);
yi = yi(t) - wielkości wyjściowe poszczególnych elementów UAR (zmienne stanu).
Układ równań (2.59) dla rzeczywistych UAR jest układem określonym i może być przekształcony w jedno równanie względem jednej zmiennej stanu (najczęściej wielkości wyjściowej y jak w równaniu (2.1)). Jeśli mieć na uwadze działanie wielkości zadanej w i zakłócenia z najczęściej rozpatrywaną postacią równania liniowego UAR jest modyfikacja (2.1)
D![]()
(2.59)
gdzie:
D = ![]()
![]()
i ![]()
liniowe operatory różniczkowe o stałych współczynnikach, przy ![]()
i ![]()
.
Dla liniowego równania różniczkowego o stałych współczynnikach obowiązuje ważna zasada superpozycji. Głosi ona, że każda wielkość wejściowa wywołuje składową wielkości wyjściowej (poszukiwanej funkcji czasu), niezależnie zarówno
od istnienia i charakteru zmian innych wielkości wejściowych jak i od warunków początkowych. Równocześnie warunki początkowe wywołują proces przejściowy, który nie zależy od wielkości wejściowych. Warunkami początkowymi równania n-tego stopnia nazywamy wartości wielkości wyjściowej i jej pochodnych do (n-1) włącznie dla t = 0.
Zasada superpozycji oznacza w szczególności, że rozwiązanie y = y(t) równania (2.59) przy warunkach początkowych ![]()
równe jest sumie trzech składowych:
![]()
(2.60)
gdzie: ![]()
, ![]()
- rozwiązania odpowiednio niejednorodnych równań:
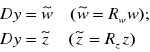
(2.61)
Przy zerowych warunkach początkowych ![]()
, a ![]()
- rozwiązanie jednorodnego równania
D![]()
(2.62)
przy zadanych warunkach początkowych![]()
![]()
Składowa ysw nazywa się składową swobodną i determinowana jest pierwiastkami równania charakterystycznego
D![]()
(2.63)
gdzie: s - zmienna zespolona.
Właściwości dynamiczne UAR ocenia się zwykle na podstawie przebiegów y(t) występujących po wprowadzeniu określonego sygnału wejściowego w(t). Wyznaczanie tych przebiegów, nazywanych krótko odpowiedziami na typowe wymuszenia, wymaga rozwiązania równania (2.1). Wykorzystuje się do tego dwie metody.
Metoda klasyczna polega na obliczeniu pierwiastków tego równania (z równania charakterystycznego (2.63)) i wyznaczeniu stałych na podstawie warunków początkowych. Ogólne rozwiązanie jednorodnego równania (2.1) ma postać sumy szczególnych rozwiązań, które zależą od pierwiastków równania charakterystycznego:
każdemu pierwiastkowi rzeczywistemu ![]()
odpowiada szczególne rozwiązanie
![]()
(2.64)
(w szczególnym przypadku ![]()
może być równe zero);
każdemu wielokrotnemu rzeczywistemu pierwiastkowi ![]()
krotności ![]()
odpowiada ![]()
rozwiązań szczególnych
![]()
(2.65)
każdej parze sprzężonych zespolonych pierwiastków ![]()
i ![]()
odpowiadają dwa rozwiązania szczególne
![]()
(2.66)
(w szczególnym przypadku ![]()
może być równe zero);
każdej parze sprzężonych zespolonych pierwiastków ![]()
i ![]()
krotności ![]()
odpowiada 2![]()
szczególnych rozwiązań
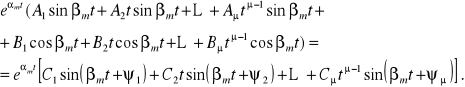
(2.67)
Stałe całkowania, wchodzące w skład rozwiązania, oznaczone literami A, B, C i ψ wyznacza się z układu równań algebraicznych spełniających warunki początkowe.
W praktyce inżynierskiej o wiele wygodniej jest stosować do rozwiązywania równań różniczkowych metodę operatorową, która pozwala znacznie uprościć tok obliczeń. Idea metody operatorowej polega na znalezieniu przekształcenia pozwalającego zastąpić równania różniczkowe zwykłymi równaniami algebraicznymi. Przekształcenie to można traktować jako prawo odpowiedniości pomiędzy dwoma zbiorami funkcji
![]()
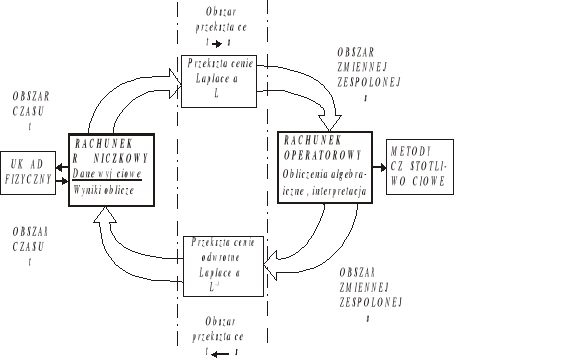
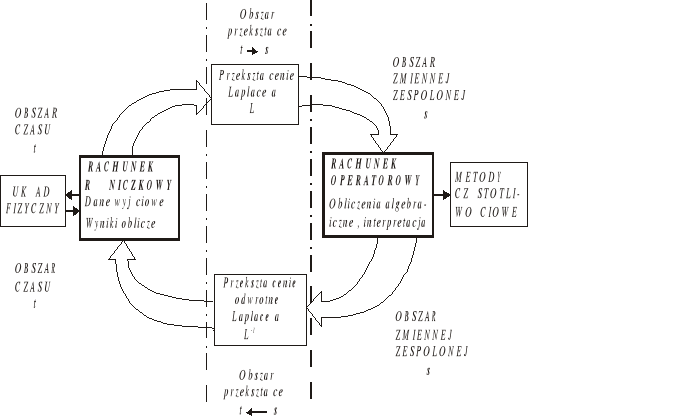
Rys. 2.8. Interpretacja graficzna przekształceń Laplace'a oraz związku rachunku różniczkowego z rachunkiem operatorowym
Ogólnie trzeba stwierdzić, że wynik rozwiązania zadania różniczkowego mieści się w przestrzeni czasu t, natomiast wynik rozwiązania tego samego zadania metodą operatorową mieści się w innej przestrzeni - zmiennej zespolonej s. Graficzna ilustracja omawianego przekształcenia przedstawiona jest na rys. 2.8.
Aby uzyskać możliwość rozwiązania zadania w przestrzeni s, trzeba je w pewnym sensie przenieś z przestrzeni t do przestrzeni s. W tej operacji przeniesienia z jednej przestrzeni do drugiej znajduje zastosowanie tzw. przekształcenie Laplace'a, zapisywane w następującej postaci
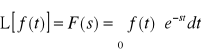
. (2.68)
Interpretacja zależności (2.68) nazywanej transformatą Laplace'a jest następująca. Funkcja f(t), określona dla t > 0, zwana oryginałem staje się pewną funkcją F(s) argumentu s, jeżeli pomiędzy funkcją f(t) a funkcją F(s) zachodzi zależność (2.68).
Właściwości rachunku operatorowego, opierającego się na przekształceniu Laplace'a, opisane są obszernie w literaturze, np. [4]. Poniżej przytoczymy podstawowe twierdzenia wynikające z (2.68), a mające znaczne zastosowanie w automatyce.
Twierdzenie o liniowości umożliwia znajdowanie oryginałów, gdy dana jest transformata F(s). Brzmi ono następująco:
transformata sumy jest równa sumie transformat
oraz
transformata iloczynu stałej i funkcji jest równa iloczynowi stałej i transformaty funkcji,
co można zapisać w następujący sposób
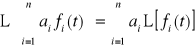
(2.69)
Twierdzenie o różniczkowaniu i całkowaniu ma znaczenie podstawowe, ponieważ
umożliwia wykonywanie działań algebraicznych w rachunku operatorowym, w którym uzyskuje się odpowiednio przekształcone równania różniczkowe i wyrażenia całkowe.
Twierdzenie o różniczkowaniu brzmi:
w rachunku operatorowym zmienna s jest nazywana operatorem różniczkowania, co można zapisać w postaci
![]()
(2.70)
Twierdzenie o całkowaniu:
w rachunku operatorowym zmienna ![]()
jest nazywana operatorem całkowania, co zapisuje się w następujący sposób
![]()
(2.71)
Twierdzenie o wartości końcowej:
Jeżeli istnieje granica funkcji f(t) dla ![]()
, to zachodzi następujący związek
![]()
(2.72)
Zależność (2.72) w praktyce umożliwia szybkie obliczanie wartości końcowej dowolnej funkcji f(t), np. wartości uchybu ![]()
w stanie ustalonym, gdy dana jest transformata wielkości wejściowej w0 oraz opis operatorowy układu regulacji.
Twierdzenie o wartości początkowej:
jeżeli istnieje granica funkcji f(t) dla ![]()
, wówczas zachodzi następujący związek
![]()
(2.73)
Interpretacja tego twierdzenia jest analogiczna do interpretacji twierdzenia poprzedniego.
5. Twierdzenie o przesunięciu rzeczywistym:
![]()
(2.74)
gdzie: τ - odcinek czasu (przesunięcie czasowe).
Rachunek operatorowy oparty o przekształcenie Laplace'a pozwala zdefiniować jedno z fundamentalnych pojęć automatyki klasycznej, a mianowicie pojęcie transmitancji operatorowej.
2.5. Transmitancja operatorowa
Transmitancją operatorową G(s) elementu lub układu nazywamy stosunek transformaty wielkości wyjściowej y(s) do transformaty wielkości wejściowej x(s) przy zerowych warunkach początkowych
![]()
(2.75)
Transformując równanie różniczkowe (2.7) opisujące właściwości elementu lub układu liniowego według zasad przedstawionych w pkt. 2.4 otrzymamy
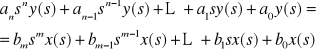
(2.76)
Zatem ogólna postać transmitancji operatorowej wyrażona będzie ilorazem dwóch wielomianów zmiennej zespolonej s
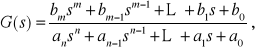
(2.77)
przy czym ![]()
.
Transmitancję tą zapisuje się często w postaci
![]()
(2.78)
gdzie
![]()
(2.78)
![]()
(2.80)
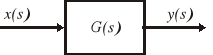
Transmitancja operatorowa (krócej: transmitancja lub często funkcja przejścia) opisuje właściwości elementu lub układu liniowego i jest równoważna równaniu różniczkowemu. Przyjęto wpisywać ją wewnątrz prostokątów symbolizujących poszczególne elementy na schematach blokowych układów automatyki (rys. 2.9).
Rys. 2.9. Schemat blokowy elementu automatyki o jednym wejściu i jednym wyjściu
Najczęściej spotykane funkcje f(t) i odpowiadające im transformaty F(s) przedstawione są w tablicy zamieszczonej w dodatku.
W praktyce zarówno transformowanie funkcji f(t), jak również znajdowanie oryginałów funkcji F(s) wymaga jedynie znajomości podstawowych twierdzeń i operowania tablicą przekształceń Laplace'a. Jedyną trudność stanowić może doprowadzenie złożonych funkcji do postaci sumy prostszych składników, mających swe odpowiedniki w tablicy przekształceń. Funkcję rozkłada się wówczas na ułamki proste, zgodnie z regułami przedstawionymi w pkt. 3.
42 2. Opis matematyczny członów i liniowych układów automatyki
Michał Chłędowski WYKŁADY Z AUTOMATYKI dla mechaników 43