Logika [logos gr.] - myśl, słowo

LOGIKA:
** zespół dyscyplin naukowych, dla których przedmiotem badań jest język i czynności badawcze (zaliczamy do nich rozumowanie, definiowanie, klasyfikowanie), których to analizę prowadzi się w celu podania takich reguł posługiwania się językiem i wykonywania owych czynności, które czyniły by tę działalność możliwie najbardziej skuteczną.

**w ścisłym tego słowa znaczeniu oznacza logikę formalną - naukę o prawach wynikania

LOGIKA:

A) Semiotyka:
semantyka
syntaktyka
pragmatyka

B) Logika formalna

C)Ogólna metodologia nauk

W skład logiki wchodzą:

A) Semiotyka - Semiotyka jest to nauka o znakach, w szczególności o znakach słownych, czyli o języku.
1. Semiotyka poddaje analizie funkcje, jakie spełnia mowa, a w szczególności zajmuje się funkcją odwzorowywania rzeczywistości przez wyrażenia mowy.
2. Przygotowuje aparat pojęciowy i terminologiczny niezbędny do zdania sprawy z różnego rodzaju uchybień przeciwko postulatom rzeczywistości i ścisłości wyrażania się,
3. Dokonuje systematycznego przeglądu tych uchybień i wskazuje środki zaradcze przeciw nim.

W skład SEMIOTYKI wchodzą:

**semantyka - ogólnie - nauka o stosunku zachodzącym między znakami językowymi, a tym, do czego te znaki się odnoszą.

Semantyka jest to dziedzina zajmująca się analizą funkcji znaczeniowych wyrażeń mowy, a przede wszystkim związkach zachodzących między wyrażeniami mowy, a myślami, które przy ich pomocy wyrażamy oraz związkami zachodzącymi między wyrażeniami, a przedmiotami, do których te wyrażenia się odnoszą [relacje semantyczne: wyrażenie - rzecz].

**syntaktyka - ogólnie - nauka o rodzajach znaków językowych regułach poprawnego wiązania tych znaków w wyrażenia złożone

Jest to część logiki, której przedmiotem są relacje zachodzące między samymi wyrażeniami języka [relacje syntaktyczne: wyrażenie - wyrażenie]

**pragmatyka - bada ona stosunki, jakie zachodzą między znakami językowymi, a tymi którzy się owymi znakami posługują. Bada stosunki między wyrażeniami językowymi, a określonym podmiotem, który te wyrażenia wytwarza lub odbiera w postaci określonego rodzaju informacji. [relacje pragmatyczne: wyrażenie - człowiek (nadawca lub odbiorca)]

B) logika formalna - przez logikę formalną rozumie się podstawowy dział logiki, w którym bada się podstawowe formy rozumowań niezawodnych, znajdujących zastosowanie we wszystkich naukach i codziennej praktyce.

Logika formalna to dziedzina pouczająca nas o związkach zachodzących między zdaniami, a przede wszystkim o tym jak ze zdań o pewnej, określonej budowie wynikają inne zdania o pewnej określonej budowie.

C) ogólna metodologia nauk - uczy jak ze zbioru twierdzeń stworzyć naukę.

1. Zajmuje się metodami - sposobami postępowania stosowanymi w zakresie poznawania świata, a przede wszystkim sposobami uzasadniania, wskazywania prawidłowości wypowiadanych twierdzeń.

2. zajmuje się także czynnościami myślowymi, które mają na celu porządkowanie naszych wiadomości w swoisty zbiór zdań tworzących dorobek jakiejś dyscypliny naukowej - wyodrębnionego działu nauki.

ŹRÓDŁA WIEDZY:

**doświadczenie [bezpośrednie]

**obserwacja [pośrednie]

WARUNKI PRZEKAZU:

**adresat

**odbiorca

**kod przekazu

ZNAK - dostrzegalny układ rzeczy czy zjawisko spowodowane przez kogoś ze względu na to, iż jakieś wyraźnie ustanowione czy zwyczajowo ukształtowane reguły nakazują wiązać z tym układem rzeczy, czy zjawiskiem myśli określonego rodzaju.

JĘZYK [jako system znaków] - jest to określony system znaków i reguł posługiwania się tymi znakami. Język jako system znaków obejmuje [wyrazy, znaczenie słów, gramatyka]:

**wyznaczony przez pewne reguły system znaków

** regały nakazujące wiązać myśli określonego rodzaju z odpowiednimi słowami

** reguły określające dopuszczalny sposób wiązania tych znaków w wyrażenia złożone.

Rodzaje języków:

A)ze względu na sposób powstania:

**naturalne -są to takie, których reguły ukształtowane zostały zwyczajowo, w sposób spontaniczny, a dopiero później ktoś podjął się odtworzenia tych reguł na podstawie obserwacji posługiwania się danym językiem przez członków jakieś grupy. [powstają samoczynnie, mają bogaty zasób słów]

**sztuczne - skonstruowane dla jakiś celów w ten sposób, ze z góry zaprojektowano ich reguły, powstaje na potrzeby określonych dyscyplin naukowych, określonych grup ludzi, później wciela się go w życie np. język prawniczy, esperanto, język mówiony) [ubogi w słownictwo, ale jest ono bardzo precyzyjne, ściśle opisuje to co ma opisać]

**mieszane

B) ze względu na stopień:

** I stopnia - język opisowy [np. jest jasno]

**n-tego stopnia jest to wypowiedz o języku stopnia n-1 [n>1, nεN] [np.2giego stopnia: ktoś powiedział ze jest jasno]

NAZWY:

**nazwami są wszystkie te i tylko te wyrazy i wyrażenia, które nadają się na podmiot lub orzecznik w zdaniach o rzeczach lub osobach.

**nazwami są wszystkie te i tylko te wyrażenia, które w zdaniach o postaci A jest B mogą być podstawione za zmienną A lub zmienną B

DESYGNAT NAZWY - jest to przedmiot, o którym zgodnie z prawdą daną nazwę możemy orzekać [przedmiot, który przy pomocy danej nazwy jest orzekany]

ZAKRES NAZWY: - zbiór wszystkich istniejących desygnatów danej nazwy;

TREŚĆ NAZWY: - zbiór tych cech, które musi posiadać przedmiot, aby można było zaliczyć go do danej grupy przedmiotów [aby był uznany za desygnat danej nazwy]

Cechy istotne [konstytutywne] są to te cechy, które pozwalają nam orzec czy dany przedmiot jest desygnatem danej nazwy.

PODZAIŁ NAZW:

**ze względu na ilość wyrazów wchodzących w skład danej nazwy:

~ proste - wyrażenia składające się tylko z jednego wyrazu

~ złożone - składają się z więcej niż jednego wyrazu

**według tego, do czego nazwa się odnosi:

~ konkretne - są to nazwy, które są znakami rzeczy lub osób, ewentualnie czegoś, co sobie wyobrażamy jako rzecz lub osobę

~abstrakcyjne - są to nazwy, które nie są znakami rzeczy czy osób, czy też czegoś, co sobie jako rzecz lub osobę wyobrażamy; wskazują one na pewną cechę wspólną wielu przedmiotów [np. szerokość, okrągłość], na pewne zdarzenie lub stan rzeczy [płacz, kradzież, cisza], albo na pewien stosunek zachodzący między przedmiotami [przyjaźń, braterstwo, niższość].

**według sposobu wskazywania desygnatów:

~generalne - są to te nazwy, które przysługują przedmiotom, ze względu na jakieś cechy, które tym przedmiotom przypisujemy, odnoszą się do wszelkich przedmiotów danego rodzaju [człowiek, wysoki człowiek]

~ indywidualne - są to nazwy, służące do oznaczenia poszczególnych, tych a nie innych przedmiotów, przy czym nie przypisują one jednocześnie danemu przedmiotowi takich czy innych właściwości wyróżniających go, nadawane są niezależnie od cech. [Rzeszów, Słońce…(nazwy własne)]

**ze względu na ilość desygnatów:

~ogólne - posiadają więcej niż jeden desygnat, np. człowiek, wieżowiec

~jednostkowe - posiadają tylko jeden desygnat

~puste - nie posiadają desygnatów [nie istnieją w rzeczywistości] np. nazwy Bogów

** ze względu na charakter zakresu nazwy:

~ostre - ściśle określony zakres nazwy

~nieostre - zakresu nazwy nie można jednoznacznie określić

np.

Mars
Treść	Bóg wojny	Planeta	Batonik
Rodzaj:	prosta	prosta	Prosta
		Konkretna	Konkretna	Konkretna
		indywidualna	indywidualna	Generalna
		Pusta	Jednostkowa	Ogólna
Desygnat:	Mars - Bóg wojny	Planeta Mars	Każdy jeden batonik o nazwie mars
Zakres	j.w	j.w	wszystkie batoniki o nazwie mars

RELACJE MIĘDZY ZAKRESAMI NAZW
Jeśli weźmiemy jakiekolwiek dwie nazwy [ograniczamy się do nazw, które mają jeden lub więcej desygnatów, pomijamy nazwy puste], nazwę S i nazwę P, i będziemy chcieli opisać jaki zachodzi stosunek między ich zakresami to trafimy na jedną z pięciu następujących możliwości:

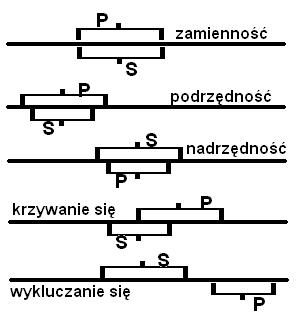
**relacja zamienności zakresów

Istnieją przedmioty, które są jednocześnie desygnatami nazwy S i nazwy P, lecz nie ma takich desygnatów nazwy S, które nie byłyby desygnatami nazwy P, i nie ma takich desygnatów nazwy P, które nie są S.

Zakres nazwy S jest zamienny [równoważny] z zakresem nazwy P wtedy i tylko wtedy gdy każdy desygnat nazwy S jest równocześnie desygnatem nazwy P i każdy desygnat nazwy P jest desygnatem nazwy A

**relacja podrzędności zakresu nazwy S względem P:

S jest podrzędne względem P wtedy i tyko wtedy, gdy desygnat nazwy S jest równocześnie desygnatem nazwy P i istnieje desygnat nazwy P nie będący desygnatem S [każde S jest P ale nie każde P jest S]

**relacja nadrzędności zakresu nazwy S względem P:

Zakres nazwy S jest nadrzędny względem zakresu nazwy P wtedy i tylko wtedy, gdy każdy desygnat nazwy P jest równocześnie desygnatem nazwy S i istnieje desygnat nazwy S nie będący desygnatem nazwy P [nie każde S jest P, ale każde P jest S]

**relacja krzyżowania się zakresy nazwy S z zakresem nazwy P:

Zakres nazwy S krzyżuje się z zakresem nazwy P wtedy i tylko wtedy gdy istnieje desygnat nazwy S będący równocześnie desygnatem nazwy P i istnieje desygnat nazwy S nie będący desygnatem nazwy P i istnieje desygnat nazwy P nie będący desygnatem nazwy S. [istnieje S nie będące P, istnieje P nie będące S i istnieje S będące P]

**relacja wykluczania się zakresu nazwy A i zakresu nazwy P:

Zakres nazwy S wyklucza się z zakresem nazwy B wtedy i tylko wtedy gdy istnieje desygnat nazwy S nie będący desygnatem nazwy P i gdy istnieje desygnat nazwy P nie będący desygnatem nazwy S, i gdy żaden desygnat S nie jest desygnatem P [istnieje S nie będące P, istnieje P nie będące S, ale nie istniej S będące P]

KATEGORIA SYNTAKTYCZNA - dwa wyrażenia należą do tej samej kategorii syntaktycznej wtedy i tylko wtedy, jeżeli po zastąpieniu jednego wyrażenia drugim, z wyrażenia sensownego otrzymujemy nadal wyrażenie sensowne. Np. zdania „Dom jest wysoki”, „Drzewo jest wysokie” należą do tej samej syntaktycznej.

Wyrażenie W₁ wzięte w znaczeniu Z₁ należy di tej samej kategorii syntaktycznej, co wyrażenie W₂ wzięte w znaczeniu Z₂ wtedy i tylko wtedy, gdy po zastąpieniu W₁ wziętym w znaczeniu Z₁, przez W₂ wziętym w znaczeniu Z₂ z wyrażenia sensownego nadal otrzymuje się wyrażenie sensowne.

Do podstawowych kategorii syntaktycznych zalicza się:

1. Zdania:

zdania

zmienne zdaniowe

funkcje zdaniowe

2. Funktory:

nazwotwórcze

zdaniotwórcze

funktorotwórcze

3. Nazwy

ZDANIA

Zdanie w sensie logicznym jest:
~wyrażenie jednoznacznie stwierdzające, na gruncie danego języka, iż tak, a tak jest albo tak, a tak nie jest;

~wyrażenie, które albo jest prawdziwe albo jest fałszywe

Wartość logiczna zdania: prawda lub fałsz

[prawda jest jedna i niezmienna, przeświadczenie o prawdzie może się zmieniać]

Kategorie Syntaktyczne zdania:

~zdanie

~zmienne zdaniowe [p,q,r,s,t,…] - zmienna zdaniowa to taka zmienna za którą możemy podstawić dowolne zdanie;

~funkcje zdaniowe - formuły zawierające zmienne i znaki stałe, a tak zbudowane, że jeżeli na miejsce zmiennych wstawimy odpowiednie stałe [zdania, nazwy] to otrzymamy zdanie w sensie logicznym.

TAUTOLOGIA - funkcja zdaniowa zawsze prawdziwa

PODZIAŁ ZDAŃ:

~zdania proste [kategoryczne] - takie wyrażenia, w których nie możemy wyróżnić mniejszej całości, która byłaby zdaniem

~zdania złożone - wyrażenia w obrębie, których możemy wyróżnić mniejszą całość, która jest zdaniem

FUNKTORY;

Funktorem jest wyrażenie nie, będące ani zdaniem, ani nazwą, a służące do wiązania nazw, zdań czy też innych wyrażeń w wyrażenia złożone.

Nazwy, zdania oraz wyrażenia wiązane danym funktorem nazywa się jego argumentami.

Podział funktorów:

**funktory nazwotwórcze - wyrażenia, które dodane do nazwy tworzą dalej nazwę:

~od jednego argumentu nazwowego - jest to wyrażenie, które dodane do nazwy tworzy nową nazwę, np. wysoki dom]

~od 2 argumentów nazwowych - wyrażenie, które łączy dwie nazwy i wyniku tego połączenia powstaje nowa nazwa np. malarz i poeta

**funktory zdaniotwórcze - wyrażenia, które łączą wyrażenia tworząc zdanie:

~od jednego argumentu nazwowego - wyrażenie, które dodane do nazwy tworzy zdanie np. Jacek je.

~od 2 argumentów nazwowych - wyrażenie, które łączy dwie nazwy tworząc zdanie, np. Jacek czyta książkę.

~od jednego argumentu zdaniowego - wyrażenie dodane do zdania tworzące nowe zdanie, np. Prawdą jest, że dzisiaj świeci słońce

~od 2 argumentów zdaniowych - wyrażenie łączące dwa zdania w wyniku czego powstaje nowe zdanie złożone, np. Pojadę do kina lub kupie książkę.

**funktory funktorotwórcze - są to takie wyrażenia, które dodane do funktora tworzą nowy funktor.

FUNKTORY PRAWDOWOŚCIOWE: - pozwalają stwierdzić wartość logiczną funkcji zdaniowej, gdy znamy wartość zmiennej zdaniowej.

~funktor negacji „~”; „nieprawdą jest, że”, „nie jest tak, że” [funktor od jednego argumentu zdaniowego]

p	~p
1	0
0	1

~funktor koniunkcji „
”, „
”; „i”, „oraz”, „ale”, „lecz”

p	q	p q
1	1	1
1	0	0
0	1	0
0	0	0

[koniunkcja jest prawdziwa gdy dwa argumenty są prawdziwe]

~alternatywa zwykła „v”; „lub”

p	q	p v q
1	1	1
1	0	1
0	1	1
0	0	0

[alternatywa zwykła jest prawdziwa gdy przynajmniej jeden z argumentów jest prawdziwy]

~alternatywa rozłączną „
”; „bądź, bądź”

p	q	p q
1	1	0
1	0	1
0	1	1
0	0	0

[alternatywa rozłączna jest prawdziwa gdy argumenty mają różną wartość]

~dysjunkcja „/” „albo, albo”

p	q	p/q
1	1	0
1	0	1
0	1	1
0	0	1

[dysjunkcja jest prawdziwa gdy przynajmniej jeden argument jest fałszywy]

~implikacja „
”; „jeżeli p to q”

p - poprzednik implikacji

q - następnik implikacji;

„a zatem”, „z tego wynika”, „tak więc” - oddziela poprzednik od następnika

p	q	p q
1	1	1
1	0	0
0	1	1
0	0	1

[implikacja jest fałszywa, gdy z prawdy wynika fałsz]

~równorzędność „
” „zawsze wtedy i tylko wtedy”

p	q	p q
1	1	1
1	0	0
0	1	0
0	0	1

Równorzędność jest prawdziwa, gdy argumenty mają tę samą wartość

UZASADNIANIE TWIERDZEŃ

Postulat racji: za prawdziwe można uznać tylko takie zdanie, dla którego można wskazać należyte uzasadnienie

Sposoby uzasadniania twierdzeń:

**bezpośrednie:

1. spostrzeżenie:

• zewnętrzne

• wewnętrzne

2. obserwacja:

• zwykła

• eksperyment

**pośrednie

1. wnioskowanie zawodne:

• redukcyjne

• z analogii

• indukcyjne:

• indukcja zupełna

• indukcja niezupełna

2. wnioskowanie niezawodne:

• bezpośrednie:

• konwersja:

• prosta

• ograniczona

• obwersja

• kontrapozycja

• częściowa

• zupełna

• w oparciu o kwadrat logiczny

• pośrednie

BEZPOŚREDNIE UZASADNIANIE twierdzeń - mamy z nim do czynienia gdy opieramy się na wynikach doświadczenia. Oparte jest na spostrzeżeniach.

SPOSTRZEŻENIE - proces poznawczy polegający na obserwowaniu przedmiotów, zjawisk świata zewnętrznego, procesów zachodzących w organizmie, powstaje w wyniku działania na nasze narządy zmysłów określonych bodźców. Bodźce dochodzące do naszych zmysłów mogą być zdeformowane [zmysły mogą deformować, mogą też one być źle zinterpretowane]

[spostrzeżenia zewnętrzne - zmysłowe - dzięki nim kontaktujemy się ze światem, który nas otacza

spostrzeżenia wewnętrzne - introspekcja - obserwacja tego co się dzieje w naszym organizmie]

OBSERWACJA - jest to dochodzenie na podstawie rozmyślnego spostrzeżenia do sądów, które mają być odpowiedzią na pewne, w danej chwili stawiane sobie pytanie.

EKSPERYMENT - złożona czynność polegająca na tym, iż staramy się wpływać na określone zjawisko, zmieniając w sposób przez nas kontrolowany warunki, w których ono przebiega, po to żeby zaobserwować, czy i jakie zmiany wystąpią w tym zjawisku przy powodowanej przez nas zmianie warunków jego przebiegu.

UZASADNIANIE POŚREDNIE - ma miejsce wówczas gdy sądy lub twierdzenia wnioskowane są z innych zdań, które wcześniej zostały wyciągnięte z innych zdań. Polega na tym, że uznaje się za prawdziwe te sądy, które wynikają ze zdań, które wcześniej zostały uznane za prawdziwe.

WNIOSKOWANIE - proces myślowy polegający na tym, że ktoś przyjmując jedno lub kilka zdań za prawdziwe dochodzi na ich podstawie do przeświadczenia o prawdziwości innego zdania.

Przesłanki - zdania, na podstawie, których uznaję się inne zdania za prawdziwe.

Wniosek - zdanie, które na podstawie wnioskowania uznaje się za prawdziwe

Przesłanka enzymatyczna, - taka, która nie jest wymieniona we wnioskowaniu
z powodu uznania jej za oczywistą.

Wnioskowanie może przebiegać według różnych schematów ogólnych zwanych schematami inferencyjnymi.

WNIOSKOWANIE

**wnioskowanie niezawodne - od prawdziwych przesłanek zawsze prowadzi do prawdziwych wniosków:

**wnioskowanie zawodne - nie zawsze od prawdziwych przesłanek prowadzi do prawdziwych wniosków

~z analogii - Jeżeli S₁ ma własność P, S₂ ma własność P, wnioskuje się, iż S₃ też ma własność P

~ indukcyjne - na podstawie wielu przesłanek jednostkowych stwierdzających, iż poszczególne zbadane przedmioty danego rodzaju mają pewną cechę, wnioskuje się, że każdy przedmiot tego rodzaju posiada taką cechę;

indukcja zupełna - mamy z nią do czynienia, jeżeli wiadomo, że nie ma innych przedmiotów danego rodzaju oprócz tych, które zostały wymienione w przesłankach jednostkowych [wnioskowanie niezawodne], jeżeli brak tej wiadomości to mamy do czynienia z indukcją niezupełną

~redukcyjne - jest to wnioskowanie, w którym z wniosku wynika przesłanka, choć z przesłanek nie wynika wniosek.

KLASYCZNE ZDANIA KATEGORYCZNE - zdania proste, podmiotowo orzecznikowe, zbudowane przy pomocy funktora „jest”.

Podział klasycznych zdań kategorycznych:

**ze względu na ilość - uwzględnia się to czy mowa jest o wszystkich desygnatach czy tylko o niektórych desygnatach nazwy będącej podmiotem zdania:

~zdania ogólne- t zdania, w których mowa o wszystkich desygnatach nazwy będącej podmiotem w rozpatrywanym zdaniu

~zdania szczegółowe - te zdania, w których mowa tylko o niektórych desygnatach nazwy będącej podmiotem w rozpatrywanym zdaniu

**ze względu na jakość - uwzględnia się to czy dane zdanie jest zdaniem twierdzącym czy przeczącym:

~zdanie twierdzące

~zdanie przeczące

4 rodzaje klasycznych zdań kategorycznych

S - nazwa będąca podmiotem, P - nazwa będąca orzecznikiem.

1. SaP zdanie ogólno twierdzące - „a” - każde jest, w którym mowa o wszystkich desygnatach danej nazwy [relacje równoważności]

Każde S jest P SaP

Tylko S jest P= Każde P jest S]

2. SeP zdanie ogólno przeczące - „e” - żadne nie jest, [relacje wykluczania się]

Żadne S nie jest P SeP

3. SiP zdanie szczegółowo twierdzące - „i” - niektóre są [wszystkie relacje oprócz wykluczania się]

Niektóre S są P SiP

4. SoP zdanie szczegółowo przeczące - „o” - niektóre nie są [relacje wykluczania, krzyżowania, nadrzędności S nad P]

Niektóre S nie są P SoP

Sposoby wnioskowań niezawodnych:

**bezpośrednie - polega na tym, że wniosek wyciąga się na podstawie tylko jednej przesłanki:

~Konwersja - rodzaj wnioskowania bezpośredniego polegającego na wyprowadzeniu z klasycznego zdania kategorycznego jego odwrócenia. Wniosek wyprowadza się odwracając przesłankę. Wyróżnia się dwa rodzaje konwersji: Konwersji nie podlegają zdania SoP

A)konwersję prostą - polega na zamianie miejscami podmiotu i orzecznika w zdaniu odwracanym. Konwersji prostej podlegają zdania:

SeP (konwersja)PeS

SiP (konwersja)PiS

Np. Niektóre ptaki (S) są wróblami (P) [zdanie SiP]

SiP (konwersja)PiS: Niektóre wróble są ptakami

B)konwersja ograniczona - polega na zamianie miejscami podmiotu i orzecznika oraz na zmianie ilości zdania odwracanego. Konwersji ograniczonej jedynie podlegają zdania:

SaP (konwersja ograniczona) PiS

~OBWERSJA - jest odmianą wnioskowania bezpośredniego, polega na wyprowadzeniu ze zdania twierdzącego równorzędnego mu zdania przeczącego na odwrót. Obwersji podlegają wszystkie rodzaje zdań kategorycznych.

Aby dokonać obwersja należy zmienić jakość zdania, a następnie zanegować orzecznik

• SaP (obwersja) Se~P

Np. Każdy stół (S) jest meblem (P) [zdanie SaP]

SaP obwersja Se~P: Żaden stół (S) nie jest meblem (P)

• SeP (obwersja) Sa~P

• SiP (obwersja) So~P

• SoP (obwersja) Si~P

~KONTRAPOZYCJA - jest to rodzaj wnioskowania bezpośredniego, powstaje przez kombinacje obwersji i konwersji. Najpierw dokonuje się obwersji, a potem konwersji.

Istnieją dwa rodzaje kontrapozycji:

A)kontrapozycja częściowa - dokonuje się przekształcając klasyczne zdanie kategoryczne wg schematu: obwersja - konwersja

• SaP (obwersja) Se~P konwersja~PeS

• SeP (obwersja) Sa~P konwersja~PiS

• SiP (obwersja) So~P konwersjanie podlega

• SoP (obwersja) Si~P konwersja~PiS

B)kontrapozycja zupełna - dokonuje się wg schematu: obwersja - konwersja - obwersja:

• SaP (obwersja) Se~P konwersja~PeS (obwersja)~Pa~S

• SeP (obwersja) Sa~P konwersja~PiS (obwersja)~Po~S

• SiP (obwersja) So~P konwersjanie podlega

• SoP (obwersja) Si~P konwersja~PiS (obwersja) ~Po~S

Np. Niektórzy mężczyźni (S) nie są studentami (P) [zdanie SoP]

• (obwersja) Si~P konwersja~PiS (obwersja) ~Po~S

Niektórzy nie studenci (~P) nie są nie mężczyznami (~S)

~KWADRAT LOGICZNY -(opozycja zdań) - jest to obrazowe przedstawienie zależności zachodzących pomiędzy klasycznymi zdaniami kategorycznymi o tym samym podmiocie i orzeczniku

Relacje w kwadracie logicznym:

~przeciwieństwa „/” np. SaP / SeP - oba mogą być jednocześnie fałszywe, nie mogą być jednocześnie prawdziwe

~podprzeciwieńśtwa „v”np. SiP v SoP - oba mogą być jednocześnie prawdziwe, nie mogą być jednocześnie fałszywe

~sprzeczności „
” np. SaP
SoP - zdania muszą mieć różną wartość nie mogą być jednocześnie fałszywe ani jednocześnie prawdziwe.

~nadrzędności „
” np. SeP
SoP,- zdanie ogólne jest nadrzędne wobec zdania szczegółowego. Jeżeli zdanie nadrzędne (ogólne) jest prawdziwe to zdanie podrzędne jest prawdziwe. Jeżeli zdanie nadrzędne jest fałszywe to zdanie podrzędne jest zdaniem nieokreślonym, może być fałszywe lub prawdziwe.

Zad 1. Przeprowadź wnioskowanie z kwadratu logicznego jeżeli wiadomo, że prawdziwe jest zdanie „Każdy adwokat jest prawnikiem”

Każdy adwokat (S) jest prawnikiem (P) SaP

SaP	„/”	SeP
1	1	0
SaP		SoP
1	1	0
SaP		SiP
1	1	1

Jeżeli wiadomo, że zdanie „Każdy adwokat jest prawnikiem” jest prawdziwe to zdanie SeP i SoP są fałszywe natomiast SiP jest prawdziwe.

Zad. 2 Przeprowadź wnioskowanie z kwadratu logicznego, jeżeli wiadomo, ze fałszywe jest zdanie sprzeczne ze zdaniem „Każdy adwokat jest prawnikiem”

Każdy adwokat (S) jest prawnikiem (P)SaP

zdanie sprzeczne do zdania SaP to zdanie SoP

SoP: Niektórzy adwokaci (S) nie są prawnikami (P)

SoP		SaP
0	1	1
SoP	v	SiP
0	1	1
SeP		SoP
0	1	0

KLASYCZNE SYLOGIZMY KATEGORYCZNE

Klasyczny sylogizm kategoryczny - wyrażenie mające postać implikacji, w której poprzednikiem jest koniunkcja dwóch klasycznych zdań kategorycznych stanowiąca przesłankę we wnioskowaniu; natomiast następnik tej implikacji w postaci klasycznego zdania kategorycznego stanowi konkluzję (wniosek).

Postacie klasycznego sylogizmu kategorycznego:

1. (PaM)
   (Mis)
   (SeP)

2. PaM

MiS

SeP

W poprawnej formule klasycznego sylogizmu kategorycznego występują trzy klasyczne zdania kategoryczne. Dwa z nich stanowią przesłankę, a trzeci jest wnioskiem, czyli konkluzją. W tych 3 klasycznych zdaniach kategorycznych występują trzy terminy czyli 3 nazwy ogólne:

~S - termin mniejszy - to nazwa, która stanowi podmiot we wniosku

~P - termin większy - nazwa będąca orzecznikiem we wniosku

~M - termin średni - to nazwa, która występuje w obydwu przesłankach, a nie występuje we wniosku.

Przesłanka mniejsza - przesłanka, w której występuje termin mniejszy - S, może być on i podmiotem i orzecznikiem w tej przesłance

Przesłanka większa - przesłanka, w której występuje termin większy - P, może być on i podmiotem i orzecznikiem w tej przesłance

Termin rozłożony - termin jest rozłożony, gdy mowa jest o wszystkich desygnatach danej nazwy [wzięty jest w całym zakresie]

~zdania SaP - rozłożony zawsze jest podmiot [Każde S jest P] - mowa o wszystkich desygnatach S

~zdania SeP - rozłożony jest podmiot i orzecznik [Żadne S nie jest żadnym P]

~zdanie SiP - nie jest rozłożony ani podmiot ani orzecznik [Niektóre S są niektórymi P]

~zdanie SoP - rozłożony jest orzecznik [Niektóre S nie są żadnymi P]

Zdania ogólne rozłożony podmiot

Zdania przeczące rozłożony orzecznik

Przykład sylogizmu:

Każdy prawnik jest człowiekiem MaP

Niektórzy prawnicy są sędziami MiS

Każdy sędzia jest człowiekiem SaP

Klasyczny sylogizm kategoryczny nie jest rozpatrywany z punktu widzenia wartości [prawda / fałsz] lecz w kategorii poprawności. Istnieje 256 wariantów sylogizmów, poprawnych jest tylko 24. Z zasady przyjmuje się, że najpierw piszę się przesłankę mniejszą, a potem większą.

Warunki poprawności sylogizmu:

1. nie może występować więcej niż 3 terminy, [poszczególne terminy nie mogą być wieloznaczne, np. gdy termin średni będzie wyrazem wieloznacznym to w każdej przesłanek będzie mógł występować w innym znaczeniu upoczwórnienie terminu]

2. termin średni w przynajmniej jednej przesłance musi być rozłożony

3. termin rozłożony we wniosku musi być rozłożony w przesłance

4. obie przesłanki nie mogą być zdaniami przeczącymi

5. obie przesłanki nie mogą być zdaniami szczegółowymi

6. jeżeli jedna z przesłanek jest zdaniem przeczącym to wniosek nie może być zdaniem twierdzącym

7. Jeżeli jedna z przesłanek jest zdaniem szczegółowym to wniosek nie może być zdaniem ogólnym

8. wniosek nie może być zdaniem przeczącym jeżeli żadna z przesłanek nie jest zdaniem przeczącym

Zdanie	Twierdzące „jest”	Przeczące „nie jest”
Szczegółowe „niektóre”	SiP	SoP
Ogólne „Każde”/ „żadne”	SaP	SeP

DEFINICJE:

I podział

**realne

**nominalne:

Definicje nominalne treściowe

Definicje nominalne zakresowe

II podział

**definicje równościowe:

klasyczne

nieklasyczne

**definicje nierównościowe

III podział

**definicje wyraźne

**definicje kontekstowe

IV podział

**definicje sprawozdawcze

**projektujące:

konstrukcyjne

regulujace

Definicja [łac.] - odgraniczenie

Definiowanie wyznaczenie granicy temu co ma być udostępnione rozumowaniu

Definicje:

**nominalne - definicją nominalną jest wyrażenie, które w ten czy w inny sposób podaje informacje o znaczeniu jakiegoś słowa czy słów. Wyjaśnia znaczenie nazwy przedmiotu. Najlepszą ilustracją definicji nominalnych są wszystkie słowniki języków obcych, w których przekłada się na język zrozumiały dla czytelnika wyraz obcojęzyczny.

Definicją nominalną posługujemy się wówczas gdy ktoś kto nie rozumie jakiegoś wyrazu lub rozumie go niewłaściwie chce się zaznajomić z właściwym jego znaczeniem.

Definicją nominalną wyrazu „w” na gruncie języka „s” jest wypowiedź pozwalająca każde zdanie zbudowane z wyrazu „w” i wyrazów słownika „s”, w którym wyraz „w” nie jest zawarty przetłumaczyć na zdanie zbudowane z samych tylko wyrazów słownika „s”.

Definicja nominalna jest wypowiedzią sformułowaną w języku II stopnia.[np. nazwa człowiek oznacza]

Rodzaje przekładów:

~treściowy - mówiąc, że wyrażenie „a” jest przekładem wyrażenia „b” można mieć na myśli, iż wyraz „a” jest równoznaczny z wyrazem „b”. [chodzi o zachowanie znaczenia tego słowa]

~przekład zakresowy - mówiąc iż wyrażenie „a” jest przekładem wyrażenia „b” można mieć na myśli, że wyrażenie „a” jest równoważne [równo - zakresowe] z wyrażeniem „b”. [w tym przypadku zachowany jest zakres wyrażenia.

W związku z tym podziałem wyróżnić można:

Definicje nominalne treściowe

Definicje nominalne zakresowe

**definicje realne - definicjami realnymi są zdania podające taką charakterystykę pewnego przedmiotu czy też przedmiotu jakiegoś rodzaju, które tym i tylko tym przedmiotom można przypisać. W przypadku tej definicji wymaga się aby zawierała ona najbardziej zwięzłą wiedzę o definiowanym przedmiocie lub grupie przedmiotów. W tym przypadku żąda się żeby była to charakterystyka ujmująca istotę definiowanego przedmiotu czy grupy przedmiotów..

np.

definicja realna: Książka jest to … (cechy istotne)

definicja nominalna: Wyraz książka oznacza …

Definicja realna jest wypowiedzą w języku w języku I stopnia - język przedmiotowy.

W definicji realnej podawane są cechy wspólne dla jakiejś uprzednio wydzielonej grupy przedmiotów. Wymaga ona, aby wcześniej wydzielić pewną grupę przedmiotów, które zaliczamy do przedmiotów danego rodzaju. Jest to spowodowane tym, iż aby móc ustalić cechę wspólną najpierw trzeba określić, z jaką grupą przedmiotów mamy do czynienia. Nie sposób, bowiem definiować czegoś, co nie jest znane.

Definicje realne rozpatrujemy z punktu widzenia ich prawdziwości lub fałszywości. Każda definicja realna jakiegoś przedmiotu wypowiada, bowiem o nim coś, co tylko o nim może być zgodnie z prawdą orzeczone.

Będzie ona prawdziwa tylko wtedy, gdy ta jednoznaczna charakterystyka, którą definicja orzeka daje się zgodnie z prawdą orzec właśnie o definiowanym przedmiocie. Będzie natomiast fałszywa w tym przypadku gdy ta charakterystyka daje się zgodnie z prawdą orzec o innych różnych od definiowanego przedmiotach.

**definicje równościowe - są to definicje podające równoznacznik dla wyrazu definiowanego. Składają się z trzech elementów

a)wyrazu definiowanego

b)ze zwrotu łączącego

c) wyrażenie definiującego

mają postać:

Wyraz X znaczy tyle co wyraz Y

Wyraz X	Znaczy tyle	Co wyraz Y
a	b	c
Definiendum	=	Definiens

Definiendum jest to wyraz lub wyrażenie w skład, którego wchodzi wyraz czy wyrażenie definiowane

Definiens jest to wyraz lub wyrażenie wyjaśniające znaczenie wyrazu czy wyrażenia definiowanego (zawartego w definiendum

„=” spójnik definicyjny - jest to zwrot stwierdzający, że definiendum ma takie samo znaczenie jak Definiens. [np. jest, jest, są, są to, znaczy tyle co, itp.]

Definicje równościowe mogą być różnie klasyfikowane:

~Definicje klasyczne - Definicja klasyczna ma postać:

A jest B mające cechy C

A- wyrażenie definiowane

B- rodzaj - wyrażenie bardziej ogólne, którego zakres jest szerszy od zakresu A

C - różnica gatunkowa

Jeżeli chcemy zdefiniować nazwę A to musimy znaleźć możliwie bliską podrzędną jej nazwę B i dookreślić treść tej nazwy poprzez określenie cechy C, tak aby desygnat nazwy B zrównał się do desygnatu nazwy A

Np.

A	Jest	B	mające cechy C
Człowiek	jest to	istota	rozumna
definiendum	=	Definiens
Definiendum	Spójnik definicyjny	Pojęcie bardziej ogólne	Różnica gatunkowa

~definicje nieklasyczne - nie będące klasycznymi

**definicje nierównościowe - są to definicje, które nie mają postaci definicji równościowych

Np. tzw. definicje aksjologiczne [x+y=12 i x-y=4 x=8 i y=4]

**ze względu na budowę definiendum definicje dzielimy na:

~definicje wyraźne - są to takie definicje, w których wyrażenie definiowane występuje samo bez żadnego kontekstu. Człon definiowany składa się jedynie z wyrazu czy też wyrażenia definiowanego. Np. Człowiek jest to istota rozumna.; Bardzo gruba książka jest to …

~definicje kontekstowe (uwikłane)- są to definicje w których wyraz czy wyrażenie definiowane występuje w typowym kontekście. Np. Logarytmem liczby przy „a” przy podstawie „b” nazywamy wykładnik „k” potęgi do której należy podnieść b aby otrzymać liczbę a.

**ze względu na zadania jakie stawiamy definicjom dzielimy je na:

~definicje sprawozdawcze - definicje które wskazują jakie znaczenie ma czy też miał kiedyś wyraz definiowany. Możemy je rozpatrywać z punktu widzenia ich prawdziwości lub fałszywości. Prawdziwą będzie def., która podaje prawdziwe znaczenie danego wyrazu

~definicje projektujące - ustalają znaczenie danego wyrazu czy wyrażenia na przyszłość. Posługujemy się nimi dla wprowadzenia do języka nowego wyrazu czy też wyrażenia lub nadania już istniejącemu wyrazowi czy wyrażeniu nowego znaczenia.

Wśród definicji projektujących wyróżniamy:

~def. konstrukcyjne - ustalają one znaczenie nowego wyrazu lub wyrażenia lub nadają całkowicie nowe znaczenie istniejącemu już wyrazowi lub wyrażeniu, Nie możemy jej rozpatrywać w kategorii prawdziwości bądź fałszywości to tylko propozycja nowej nazwy

~def. regulujące - ustalają one na przyszłość wyraźne znaczenie istniejącego wyrazu licząc się jednak z jego dotychczasowym znaczeniem. Używamy ich gdy z terminu nieostrego tworzymy ostry.

WARUNKI POPRAWNOŚCI DEFINICJI:

1. definicja musi być zdaniem prawdziwym.

Definicja sprawozdawcza stanowi zdanie w sensie logicznym, więc można stosować do niej kryterium prawdziwości. Definicja projektująca jak i regulująca nie stanowi zdania w sensie logicznym [nie jest wiec ani prawdziwa ani fałszywa]. Definicja projektująca ustala bowiem znaczenie nowego terminu, a jej twórca proponuje by od tej pory taki, a taki przedmiot nazywać tak a tak.

Pod adresem twórcy definicji regulującej zgłasza się postulat by nadając wyrazom nie ostym umownie sprecyzowany ścisły sens nie odbiegać zbytnio od obowiązującego w języku potocznym lub naukowym znaczenia definiowanego wyrazu.

Jeżeli wyrażeniem definiowanym jest nazwa to w tym przypadku warunek prawdziwości definicji można sprowadzić do tożsamości zakresowej członu definiowanego.

2. Definicja musi być informująca

Definiens powinien zawierać wyrazy zrozumiałe i jasne.

Jest to postulat względny, wchodzi tu, bowiem w grę odbiorca definicji. Inaczej można definiować jakiś wyraz gdy podajemy jego znaczenie fachowcowi z danej dziedziny, a inaczej trzeba definiować do znaczenie tego wyrazu dla laika.

Definicja jest informująca jeżeli termin definiujący jest zrozumiały dla osoby, dla której daną definicję podajemy na gruncie danego języka.

W przypadku, gdy celem definicji jest pogłębienie rozumienia wyrazu definiowanego człon definiujący musi podawać więcej informacji niż definiendum.

3 definicja musi być tak sformułowana by była wypowiedzią maksymalnie zwięzłą:

Rezultat ten osiąga się przez odpowiedni dobór cech. Chodzi tu o wybór takich cech, który by maksymalnie informował, a jednocześnie było ich jak najmniej „minimum słów, maximum treści”

Do błędów najczęściej występujących przy definiowaniu zalicza się:

**błąd „nieznane przez nieznane” - występuje on wówczas, gdy definiens zawiera wyraz niezrozumiały dla odbiorcy definicji. Błędu tego nie popełnia ten, kto umieszcza w części definiującej wyrażenie niezrozumiałym, a następnie zwrot ten definiuje osobno.

**”to samo przez to samo” -tzw. błędne koło bezpośrednie; błąd ten występuje wtedy gdy definiens i definiendum zawierają wyraz definiowany

**”błędne koło pośrednie” - błąd ten występuje wówczas gdy wyraz „a” definiujemy przy pomocy wyrazu „b” [a jest b],; b definiujemy przy pomoce c [b jest c], a „c” przy pomocy „a” [c jest a]

Poprawna definicja równościowa musi być adekwatna definiens i definiendum powinny posiadać zakresy równoważne.

Definicja jest nieadekwatna gdy zakresy te nie pokrywają się. Taka sytuacja będzie miałą miejsce gdy:

~definicja jest za szeroka ­ definiens ma zakres nadrzędny w stosunku do zakresu definiendum.

~definicja za wąska- definiens ma zakres podrzędny w stosunku do zakresu definiendum

KONIEC

P.S w razie napotkania wybitnie rażących błędów proszę o uprzejmy donos na adres [e-mail]

1

---