ROZDZIAŁ 8.
WERYFIKACJA HIPOTEZ STATYSTYCZNYCH W RACHUNKU KORELACJI I REGRESJI
8.1. Wstęp
Rachunek korelacji i regresji zajmuje się, jak wiadomo, badaniem zależności między zmiennymi. W rachunku tym testy statystyczne mogą więc być stosowane do weryfikacji następującego rodzaju hipotez:
Czy siła zależności między badanymi zmiennymi jest statystycznie istotna?
Czy ilościowe oddziaływanie danej zmiennej objaśniającej na zmienną objaśnianą ma określony wymiar, w szczególnym przypadku, czy jest statystycznie istotne?
Czy można przyjąć, że funkcja regresji ma postać liniową?
Do weryfikacji wymienionych hipotez można wykorzystać wiele testów. Należą do nich:
test t na istotność współczynnika korelacji liniowej,
test t na istotność współczynnika korelacji cząstkowej,
test F na istotność współczynnika korelacji wielorakiej,
test niezależności 2,
test na istotność współczynnika regresji liniowej dwóch zmiennych i współczynnika regresji cząstkowej,
test serii na liniowość funkcji regresji.
Wśród tych testów, jak można zauważyć, są zarówno testy parametryczne, jak i nie-parametryczne.
8.2. Testy istotności dla współczynnika korelacji liniowej i współczynnika regresji liniowej
Testy te stosujemy w przypadku, gdy zbiorowość analizowana jest ze względu na dwie zmienne, między którymi badamy zależność. W szczególności interesuje nas, czy jest to zależność liniowa.
W przypadku testu dla współczynnika korelacji sprawdzamy hipotezę, że zmienne X i Y nie są skorelowane. Miarą tej zależności jest współczynnik korelacji liniowej oznaczany dla populacji generalnej symbolem ρ , stąd hipoteza zerowa ma postać:
![]()
, (8.1)
wobec hipotezy alternatywnej, która przyjmuje jedną z trzech możliwych postaci:
![]()
lub ![]()
lub ![]()
(8.2)
W celu weryfikacji hipotezy zerowej z populacji generalnej losujemy próbę liczącą n elementów i liczymy współczynnik korelacji z próby r według wzoru:
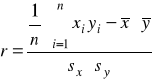
. (8.3)
Następnie liczymy wartość sprawdzianu hipotezy zerowej zgodnie ze wzorem:
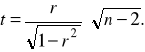
(8.4)
Statystyka ta, przy założeniu prawdziwości hipotezy zerowej, ma rozkład t-Studenta o n-2 stopniach swobody.
Z tablic rozkładu t-Studenta, dla założonego poziomu istotności i n-2 stopni swobody odczytujemy wartość krytyczną t.
W zależności od postaci hipotezy alternatywnej możemy tu mieć do czynienia z dwu-stronnym, prawostronnym lub lewostronnym obszarem krytycznym.
Gdy hipoteza alternatywna ma postać: ![]()
(dwustronny obszar krytyczny), to odczytujemy ![]()
, a H0 odrzucamy na rzecz H1 gdy: ![]()
W przypadku, gdy ![]()
(obszar krytyczny prawostronny), odczytujemy: ![]()
, to H0 odrzucamy na rzecz H1, gdy: ![]()
natomiast gdy ![]()
(lewostronny obszar krytyczny) odczytujemy wartość ![]()
, nadajemy jej znak „minus” a hipotezę zerową odrzucamy, gdy spełniona jest nierówność: ![]()
Odrzucenie hipotezy zerowej oznacza, że zależność między badanymi zmiennymi jest statystycznie istotna.
O tym, czy zależność między dwiema badanymi zmiennymi jest istotna można też wnioskować wykorzystując test istotności dla współczynnika regresji liniowej.
W teście tym stawiamy hipotezę zerową, że współczynnik regresji w populacji generalnej jest równy pewnej postulowanej wartości, czyli hipoteza brzmi:
![]()
(8.5)
wobec hipotezy alternatywnej, która, podobnie jak w poprzednim teście, może mieć trzy postaci:
![]()
lub ![]()
lub ![]()
(8.6)
Dla weryfikacji hipotezy zerowej z populacji generalnej losujemy n-elementową próbę, na podstawie której szacujemy funkcję regresji liniowej:
![]()
(8.7)
Następnie liczymy sprawdzian hipotezy zerowej według wzoru:
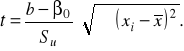
(8.8)
We wzorze tym Su oznacza odchylenie standardowe składnika resztowego funkcji regresji liczone według wzoru:
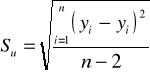
, (8.9)
gdzie:
yi - empiryczne wartości zmiennej objaśnianej dla i = 1, 2, …, n,
![]()
- teoretyczne wartości zmiennej objaśnianej dla i = 1, 2, …, n.
Statystyka t, przy założeniu prawdziwości hipotezy zerowej, ma rozkład t-Studenta o n-2 stopniach swobody.
Wartość tej statystyki porównujemy z wartością t według takich samych zasad jak poprzednio (w teście istotności dla współczynnika korelacji).
8.3. Test na liniowość funkcji regresji dwóch zmiennych
Populację generalną badamy z uwagi na dwie zmienne: X i Y. Z populacji tej losujemy próbę, która liczy n elementów. Na podstawie wyników tej próby mamy zweryfikować hipotezę, że funkcja regresji Y względem X w populacji generalnej jest liniowa.
Stawiamy hipotezę zerową:
![]()
, (8.10)
oraz hipotezę alternatywną:
![]()
(8.11)
Na podstawie wyników z próby szacujemy funkcję regresji liniowej postaci:
![]()
. (8.12)
Parametry tej funkcji liczymy według wzorów:
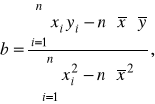
![]()
(8.13)
Następnie obliczamy wartości funkcji regresji ![]()
dla wszystkich ustalonych dla próby wartości zmiennej objaśniającej xi (i = 1, 2, … , n).
W tablicy roboczej porządkujemy rosnąco, według wartości zmiennej objaśniającej, dane
z trzech kolumn, które zawierają: xi, yi oraz ![]()
.
Porównujemy wartości yi oraz ![]()
.
Jeżeli ![]()
to takiej relacji przypisujemy symbol a. Jeśli zaś ![]()
to symbol b.
Otrzymujemy ciąg symboli a oraz b. Ustalamy liczbę serii w tym ciągu i oznaczamy ją przez k. Jest ona sprawdzianem hipotezy zerowej.
Porównujemy ją z wartością krytyczną liczby serii k odczytaną z tablic rozkładu liczby serii dla założonego poziomu istotności oraz na (liczba symboli a w ciągu) i nb (liczba symboli b w ciągu).
Gdy zajdzie relacja: ![]()
to stwierdzamy, że nie ma podstaw do odrzucenia hipotezy zerowej, że funkcja regresji Y względem X w populacji generalnej jest liniowa.
Przykład 8.1
W celu zbadania zależności między wydajnością pracy i stażem pracy pracowników pewnego zakładu przemysłowego wylosowano próbę 10 pracowników i otrzymano dla nich następujące dane:
Staż pracy - xi |
1 |
2 |
3 |
8 |
5 |
6 |
7 |
8 |
9 |
10 |
Wydajność pracy - yi (sztuki/godz.) |
10 |
15 |
13 |
22 |
23 |
20 |
18 |
25 |
27 |
22 |
Źródło: dane umowne.
Przyjmując = 0,05 zweryfikuj następujące hipotezy:
czy między wydajnością pracy a stażem pracy występuje statystycznie istotna zależność liniowa?
Czy wzrost stażu o 1 rok pociąga za sobą przeciętny wzrost wydajności pracy o więcej niż 1,3 szt./godz?
Czy funkcja regresji wydajności pracy względem stażu pracy jest liniowa?
Rozwiązanie:
Ad. a) Należy zastosować test istotności dla współczynnika korelacji liniowej.
Stawiamy hipotezę zerową i alternatywną:
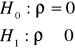
(8.14)
Sprawdzian hipotezy zerowej ma postać:
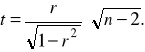
(8.15)
Stąd musimy najpierw wyliczyć współczynnik korelacji z próby.
Potrzebne obliczenia wykonujemy w tabeli roboczej 8.1.1.
Tabela robocza 8.1.1.
|
|
|
|
|
1 2 3 8 5 6 7 8 9 10 |
10 15 13 22 23 20 18 25 27 22 |
10 30 39 176 115 120 126 200 243 220 |
1 4 9 64 25 36 49 64 81 100 |
100 225 169 484 529 400 324 625 729 484 |
59 |
195 |
1279 |
433 |
4069 |
Źródło: obliczenia własne.
Liczymy średnie i odchylenia standardowe obu zmiennych:
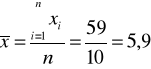
; 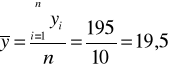
;
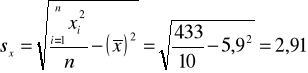
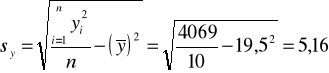
.
Następnie liczymy współczynnik korelacji liniowej z próby:
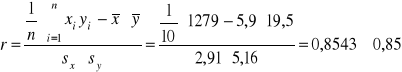
.
Teraz możemy wyliczyć wartość sprawdzianu hipotezy zerowej:
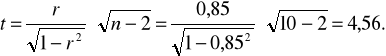
W tablicach rozkładu t-Studenta dla = 0,05 oraz n-2 stopni swobody odczytujemy wartość krytyczną t: ![]()
.
Odpowiedź:
Ponieważ ![]()
wobec tego hipotezę zerową odrzucamy na korzyść hipotezy alternatywnej. Oznacza to, że liniowa zależność między stażem pracy a wydajnością pracy jest statystycznie istotna.
Ilustracja graficzna:
Ad. b) Zastosujemy test istotności dla współczynnika regresji liniowej.
Stawiamy hipotezę zerową i alternatywną:
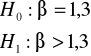
(8.16)
Na podstawie wyników próby szacujemy funkcję regresji liniowej: ![]()
Wykorzystując obliczenia wykonane w tabeli roboczej 1 wyznaczamy wartości para-metrów tej funkcji:
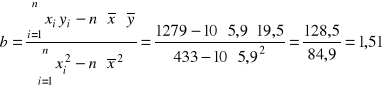
,
![]()
.
Funkcja ma więc postać: ![]()
.
Liczymy wartości teoretyczne![]()
, a następnie odchylenie standardowe składnika resztowego funkcji regresji Su. Konieczne obliczenia zamieszczone są w tabeli roboczej 8.1.2.
Tabela robocza 8.1.2.
|
|
|
|
|
Symbole |
1 |
2 |
3 |
4 |
5 |
6 |
1 2 3 8 5 6 7 8 9 10 |
10 15 13 22 23 20 18 25 27 22 |
12,11 13,62 15,13 22,68 18,15 19,66 21,17 22,68 24,19 25,70 |
4,4521 1,9044 4,5369 0,4634 23,5225 0,1156 10,0489 5,3824 7,8961 13,6900 |
24,01 15,21 8,41 4,41 0,81 0,01 1,21 4,41 9,61 16,81 |
a b a a b b a b b a |
59 |
195 |
X |
72,0113 |
84,90 |
X |
Źródło: obliczenia własne.
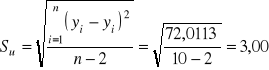
Liczymy wartość sprawdzianu hipotezy zerowej:
![]()
Z tablic rozkładu t-Studenta odczytujemy wartość krytyczną t dla n -2 stopni swobody oraz założonego poziomu istotności. Obszar krytyczny jest prawostronny, stąd odczy-tujemy: ![]()
.
Odpowiedź:
Ponieważ ![]()
, więc nie ma podstaw do odrzucenia H0.
Oznacza to, że nie jest prawdą, że wzrost stażu o rok wiąże się ze wzrostem wydajności o więcej niż 1,3 szt./godz.
Ilustracja graficzna:
Ad. c) Stosujemy test serii.
Stawiamy hipotezę zerową i alternatywną:
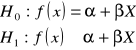
(8.17)
Obserwacje z próby są z założenia uporządkowane rosnąco według wartości cechy X.
W tabeli roboczej 8.1.2 zostały też wyliczone wartości ![]()
, stąd możemy przystąpić do nadawania symboli a i b. Jest to wykonane w kolumnie 6 tabeli roboczej 8.1.2.
Liczba serii w ciągu wynosi 7. Jest to sprawdzian hipotezy zerowej.
Z tablic rozkładu liczby serii odczytujemy wartość krytyczną k dla założonego poziomu istotności = 0,05 oraz dla na = 5 oraz nb = 5 wynosi ona ![]()
Odpowiedź:
Ponieważ ![]()
, nie ma więc podstaw do odrzucenia H0.
Można w związku z tym przyjąć, że funkcja regresji wydajności pracy względem stażu pracy jest liniowa.
8.4. Test niezależności
Test ten stosujemy do weryfikacji hipotezy, że dwie zmienne w populacji generalnej są niezależne. Ma on zastosowanie, gdy przynajmniej jedna z tych zmiennych jest niemierzalna.
Zmienne są niezależne, gdy dla dystrybuant zachodzi równość ![]()
. Stąd hipotezy w tym teście można zapisać:
![]()
![]()
, (8.18)
H1: ![]()
. (8.19)
Sprawdzianem hipotezy zerowej jest statystyka:
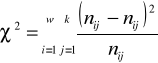
, (8.20)
gdzie:
![]()
- liczebności empiryczne znajdujące się na przecięciu i-tego wiersza i j-tej kolumny w tablicy kontyngencji,
![]()
- liczebności teoretyczne znajdujące się na przecięciu i-tego wiersza i j-tej kolumny w tablicy kontyngencji.
Liczebności teoretyczne liczone są według wzoru:
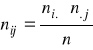
dla i = 1, 2, ,,,, w ; j = 1, 2, …, k. (8.21)
gdzie:
![]()
- liczebność brzegowa obliczona dla i-tego wiersza po wszystkich kolumnach tablicy kontyngencji,
![]()
- liczebność brzegowa obliczona dla j-tej kolumny po wszystkich wierszach tablicy kontyngencji.
Statystyka ma, przy założeniu prawdziwości hipotezy zerowej, rozkład o (k-1)(w-1) stopniach swobody. Jej wartość porównujemy więc z wartością krytyczną ![]()
odczytaną z tablic tego rozkładu dla założonego poziomu istotności i (k-1)(w-1) stopni swobody. Jeśli ![]()
, to H0 odrzucamy na korzyść H1, czyli między badanymi zmiennymi występuje zależność.
Żeby omawiany test zastosować trzeba zbudować tablicę kontyngencji, która ma następującą postać:
Warianty |
Warianty cechy Y |
ni. |
|||
cechy X |
y1 |
y2 |
... |
yk |
|
x1 |
n11 |
n12 |
... |
n1k |
n1. |
x2 |
n21 |
n22 |
... |
n2k |
n2. |
... |
... |
... |
... |
... |
... |
xw |
nw1 |
nw2 |
... |
nwk |
nw. |
n.j |
n.1 |
n.2 |
... |
n.k |
n |
Przykład 8.2
Postawiono hipotezę, że istnieje zależność między wielkością firmy (małe i mikro) a jej wynikiem finansowym. W celu sprawdzenia tej hipotezy wylosowano 100 firm, wśród których było 70 mikro-firm. Spośród wylosowanych, zysk w badanym okresie osiągnęło 60 firm, zaś stratę poniosło 20 firm małych.
Czy hipoteza jest prawdziwa? Przyjmij = 0,05.
Rozwiązanie:
Stosujemy test niezależności 2.
Stawiamy hipotezę zerową i alternatywną:
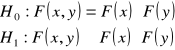
(8.22)
Budujemy tablicę kontyngencji:
Wynik finansowy ( xi ) |
Typ firmy ( yi ) |
ni. |
|
|
mikro |
mała |
|
Zysk |
50 |
10 |
60 |
Strata |
20 |
20 |
40 |
n.j |
70 |
30 |
100 |
Źródło: dane z przykładu 8.2.
Obliczamy liczebności teoretyczne ![]()
:
![]()
, ![]()
,
![]()
, ![]()
.
Zestawiamy w tabeli roboczej 8.2. liczebności empiryczne i teoretyczne, a następnie liczymy statystykę 2.
Tabela robocza 8.2.
i, j |
|
|
|
1,1 1,2 2,1 2,2 |
50 10 20 20 |
42 18 28 12 |
1,52 3,56 2,29 5,33 |
Ogółem |
100 |
100 |
12,70 |
Źródło: obliczenia własne.
Mamy, że ![]()
Z tablic rozkładu 2 odczytujemy wartość krytyczną dla = 0,05 oraz ![]()
=1 stopni swobody. Wynosi ona: ![]()
Odpowiedź:
Ponieważ ![]()
wobec tego H0 odrzucamy na rzecz H1.
Oznacza to, że pomiędzy badanymi zmiennymi występuje istotna zależność.
Ilustracja graficzna:
Weryfikacja hipotez w rachunku korelacji i regresji wielorakiej
W przypadku, gdy badamy zależność między zmienną Y a ciągiem zmiennych objaśniających Xj (j = 1, 2, … , k), to otrzymujemy wówczas model regresji wielokrotnej postaci:
![]()
. (8.23)
Zależność badamy najczęściej opierając się na wynikach uzyskanych dla próby losowej pobranej z populacji generalnej.
W takim przypadku najczęściej weryfikujemy hipotezy dotyczące:
istotności wpływu poszczególnych zmiennych objaśniających na zmienną objaśnianą,
istotności współczynnika korelacji wielorakiej R*, określającego łączny wpływ wszystkich zmiennych objaśniających na zmienną objaśnianą.
Dla weryfikacji hipotezy o istotności współczynników regresji cząstkowej j wykorzystujemy test t-Studenta.
Stawiamy hipotezę zerową: ![]()
wobec ![]()
.
Następnie stosując KMNK szacujemy, na podstawie wyników próby, parametry modelu regresji wielokrotnej otrzymując oceny parametrów tego modelu aj.
Sprawdzian hipotezy zerowej w tym teście liczymy według wzoru:
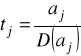
, (8.24)
gdzie:
D (aj) - średni błąd szacunku parametru o numerze j (j = 1, 2, … , k).
Sprawdzian ten, przy założeniu prawdziwości hipotezy zerowej ma rozkład t-Studenta o n-k stopniach swobody. Stąd jego wartość porównujemy z wartością krytyczną t odczytaną z tablic rozkładu t-Studenta dla założonego oraz n - k stopni swobody, gdzie k jest liczbą parametrów modelu łącznie z wyrazem wolnym.
Jeśli okaże się, że ![]()
, to hipotezę zerową odrzucamy na korzyść H1. Oznacza to, że zmienna Xj istotnie wpływa na zmiany zmiennej objaśnianej.
Dla weryfikacji z kolei hipotezy zerowej o istotności współczynnika korelacji wielokrotnej R* wykorzystujemy test F.
Stawiamy H0: R* = 0 wobec H1: R* > 0.
Na podstawie próby liczącej n elementów obliczamy współczynnik korelacji wielokrotnej R, a następnie liczymy sprawdzian hipotezy zerowej, który ma postać:
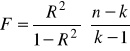
. (8.25)
Sprawdzian ten, przy założeniu prawdziwości hipotezy zerowej, ma rozkład F Fishera-Snedecora o (n-k) oraz (k-1) stopniach swobody. Odczytujemy więc wartość krytyczną F z tablic tego rozkładu dla założonego poziomu istotności i wspomnianej liczby stopni swobody.
Jeśli F > F , to H0 odrzucamy ma korzyść H1. Oznacza to, że zależność między zmienną Y a zmiennymi X1, X2,…, Xk jest statystycznie istotna.
Przykład 8.3
Z populacji generalnej pobrano próbę liczącą 25 elementów i na jej podstawie oszacowano model regresji wielokrotnej.
![]()
.
Przyjmując = 0,05 sprawdź istotność parametru 1 tego modelu oraz istotność współczynnika korelacji R*, który wyniósł dla próby 0,85.
Rozwiązanie:
Dla sprawdzenia hipotezy o istotności parametry 1 zastosujemy test t-Studenta. Stawiamy hipotezę zerową i hipotezę alternatywną:
![]()
![]()
. (8.26)
Liczymy wartość sprawdzianu hipotezy zerowej:
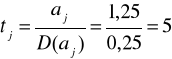
.
Z tablic rozkładu t-Studenta odczytujemy dla = 0,05 oraz n - k = 25 - 3 = 22 stopni swobody wartość krytyczną t = 2,074.
Odpowiedź:
Ponieważ zachodzi: ![]()
, więc H0 odrzucamy ma korzyść H1.
Oznacza to, że zmienna X1 w sposób istotny wpływa na zmienną objaśnianą Y.
Ilustracja graficzna:
Dla weryfikacji z kolei hipotezy o istotności współczynnika korelacji wielokrotnej stosujemy test F - Fishera. Stawiamy H0 i H1:
H0: R* = 0 H1: R* > 0. (8.27)
Liczymy sprawdzian hipotezy zerowej:
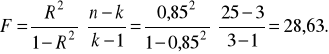
Z tablic rozkładu F - Fishera odczytujemy następnie dla założonego poziomu istotności oraz 22 i 2 stopni swobody wartość krytyczną F = 3,44.
Odpowiedź:
Ponieważ ![]()
, więc hipotezę zerową odrzucamy na korzyść hipotezy alternatywnej. Oznacza to, że łączny wpływ wszystkich zmiennych objaśniających na zmienną objaśnianą jest statystycznie istotny.
Ilustracja graficzna:
Zadania
Zadanie 8.1
W roku akademickim 2007/2008 na II roku studiów dziennych jednego z wydziałów pewnej uczelni w Poznaniu było 500 studentów, w tym 180 mężczyzn. Letnią sesję egzaminacyjną bez poprawek zaliczyło 350 studentów, w tym 100 mężczyzn.
Czy istnieje zależność między wynikami sesji a płcią studentów ? (Przyjmij α = 0,05).
Zadanie 8.2
Zamieszczona tabela wielodzielcza przedstawia zaobserwowane liczebności warunkowe dotyczące zawodów ojca i syna w 250 rodzinach pracowniczych.
Zawód ojca |
Zawód syna |
||
|
nauczyciel |
ekonomista |
inżynier |
Nauczyciel |
30 |
10 |
40 |
Ekonomista |
20 |
40 |
20 |
Inżynier |
10 |
30 |
50 |
Źródło: dane umowne.
Czy można na tej podstawie stwierdzić, że wybór zawodu przez syna zależy od zawodu ojca (α = 0,01)?
Zadanie 8.3
W roku 2008 przedsiębiorstwo żeglugowe A posiadało 80 statków zatrudnionych w żegludze regularnej i 10 statków zatrudnionych w trampingu, natomiast przedsiębiorstwo B odpowiednio 40 statków zatrudnionych w żegludze regularnej i 20 w trampingu.
Sprawdź czy występuje współzależność między typem przedsiębiorstwa a charakterem zatrudnienia floty? (Przyjmij α = 0,10).
Zadanie 8.4
Zbadano 200 gospodarstw domowych w powiecie „Z” w celu określenia, czy występuje współzależność między liczbą osób w gospodarstwie domowym a przynależnością do grupy społeczno-ekonomicznej.
Wyniki badania zestawiono w poniższej tabeli wielodzielczej.
Grupa społeczno- |
Liczba osób w gospodarstwie |
||
-ekonomiczna |
1 |
2 |
3 i więcej |
Pracowników |
2 |
50 |
20 |
Rolników |
2 |
8 |
30 |
Pracujących na własny rachunek |
10 |
4 |
12 |
Emerytów i rencistów |
40 |
20 |
2 |
Źródło: dane umowne.
Zweryfikuj hipotezę, że związek między wyróżnionymi zmiennymi jest statystycznie istotny (α = 0,05).
Zadanie 8.5
W pewnym przedsiębiorstwie przeprowadzono badanie zależności między wydajnością pracy robotników [szt./godz.] a ich stażem pracy [lata].
Na podstawie wyników otrzymanych dla 100-osobowej próby robotników ustalono, że:
średnia wydajność wyniosła 40 szt./godz., a odchylenie standardowe wydajności stanowi 25% średniego jej poziomu,
przeciętny przyrost wydajności na jednostkę (1 rok) przyrostu stażu pracy wynosi 2 szt./godz.,
empiryczny rozkład stażu pracy jest następujący:
Czy zależność między badanymi zmiennymi jest statystycznie istotna (α = 0,05)?
Czy staż pracy jest statystycznie istotną zmienną objaśniającą (α = 0,05)?
czy korelację między wydajnością pracy robotników, a czasem ich nieprzerwanej pracy można uznać za statystycznie istotną, przy poziomie istotności 0,10 ?
czy można przyjąć, że funkcja regresji wydajności względem czasu nieprzerwanej pracy robotników jest liniowa (α = 0,05) ?
wzrost skali produkcji o 1 sztukę prowadził do spadku kosztu jednostkowego przeciętnie o 270 zł,
łączna produkcja wyrobu Z w badanych zakładach wyniosła 200 szt., a łączne koszty jednostkowe 75 tys. zł.
średni staż pracy wyniósł 10 lat,
staż pracy w 81 % wyjaśnia zmienność liczby braków,
w celu zmniejszenia liczby braków potrzeba wydłużenia stażu pracy, przeciętnie biorąc o 0,3 roku,
teoretycznie biorąc przy liczbie braków równej 0 sztuk, staż pracy wynosi 13 lata.
średnia arytmetyczna = 19,4 tys. zł,
odchylenie standardowe = 4 tys. zł,
r = 0,8.
określ łączny wpływ zmiennych X1 i X2 na zmienną Y, w badanej grupie gospodarstw domowych i zbadaj czy jest on statystycznie istotny (α = 0,01),
sprawdź istotność współczynnika korelacji częściowej wydatków względem dochodu (α = 0,10).
Oszacuj równanie regresji wielokrotnej, opisujące zależność liczby przestępstw na 1000 mieszkańców tego kraju od podanych zmiennych i ustal, czy ich wpływ jest statystycznie istotny przy poziomie istotności 0,05.
Ustal wartość współczynnika korelacji wielorakiej i zbadaj jego istotność.
czy funkcja spożycia na badane dobro powinna zawierać obie zmienne objaśniające? Uzasadnij odpowiedź. (Przyjmij α = 0,10).
Oszacuj właściwą funkcję spożycia.
Które ze zmiennych objaśniających powinny się znaleźć, twoim zdaniem, w modelu regresji?
Utwórz równanie regresji y względem dwóch „najlepszych” zmiennych objaśniających wiedząc, że α0 = 10.
Staż pracy |
Liczba robotników |
0 - 4 |
5 |
4 - 8 |
25 |
8 - 12 |
35 |
12 - 16 |
20 |
16 - 20 |
15 |
× |
100 |
Źródło: dane umowne.
Zadanie 8.6
W zakładzie Z wysunięto hipotezę, że wydajność pracy robotników zależy od czasu nieprzerwanej pracy robotników w ciągu dnia roboczego. W celu sprawdzenia tego przypuszczenia pobrano próbę liczącą 10 robotników i otrzymano następujące dane:
Wydajność pracy [kg/godz] |
18 |
20 |
18 |
17 |
15 |
15 |
14 |
12 |
10 |
9 |
Czas nieprzerwanej pracy [godz.] |
2 |
3 |
3 |
4 |
5 |
6 |
7 |
11 |
9 |
10 |
Źródło: dane umowne.
Zadanie 8.7
Na podstawie wyników 27-elementowej próby gospodarstw domowych zamieszkujących na os. Stefana Batorego w Poznaniu zbadano zależność między wydatkami na artykuł Z (Y) a liczbą osób w gospodarstwie domowym (X).
Otrzymano następującą funkcję regresji: ![]()
. Równocześnie wiadomo, że odchylenie standardowe składnika resztowego Su = 0,7, a odchylenie standardowe zmiennej X wynosi 1,3. Przyjmując poziom istotności 0,05, zweryfikuj hipotezę o istotności współczynnika regresji.
Zadanie 8.8
Całkowite koszty produkcji i wielkość produkcji w 7 przedsiębiorstwach należących do tej samej branży były następujące :
Koszty [tys. zł ] |
52 |
54 |
63 |
60 |
88 |
90 |
100 |
Produkcja [tys. zł] |
20 |
30 |
40 |
101 |
183 |
190 |
200 |
Źródło: dane umowne.
Czy można przyjąć, że funkcja regresji kosztów względem produkcji jest liniowa ?
Uzasadnij odpowiedź.
Zadanie 8.9
Przeprowadzono badanie zależności między długością serii produkcji artykułu Z [szt.] a kosztem jednostkowym produkcji tego wyrobu [zł] w 25 zakładach go wytwarzających.
Okazało się, że jest to zależność o kształcie liniowym, przy czym:
Czy współzależność między badanymi zmiennymi jest statystycznie istotna (α = 0,05)?
Zadanie 8.10
Badanie zależności między liczbą braków [szt.] powstałych przy wytwarzaniu pewnego detalu w grupie 15 pracowników pewnego zakładu a ich stażem pracy dało następujące rezultaty:
Wiedząc, że związek korelacyjny między badanymi zmiennymi jest liniowy sprawdź istotność współczynnika korelacji (α = 0,10),
Zadanie 8.11
Mając informacje o tygodniowych płacach i stażu pracy 10 pracowników zatrudnionych
w pewnym zakładzie, ustal siłę i kierunek związku korelacyjnego między tymi zmiennymi.
Płace [zł] |
300 |
500 |
405 |
400 |
505 |
500 |
605 |
600 |
600 |
500 |
Staż pracy [lata] |
1 |
5 |
3 |
3 |
7 |
4 |
10 |
10 |
8 |
6 |
Źródło: dane umowne.
Sprawdź, przy poziomie istotności α = 0,10, czy zależność pomiędzy badanymi zmiennymi jest liniowa.
Zadanie 8.12
Struktura 25 sklepów ogólnospożywczych według wysokości obrotów w Poznaniu w roku 2002 była następująca :
Obroty [tys. zł] |
Liczba sklepów |
40-60 |
5 |
60-80 |
12 |
80-100 |
6 |
100-120 |
2 |
x |
25 |
Źródło: dane umowne.
Natomiast rozkład empiryczny kosztów handlowych w tych sklepach opisują poniższe parametry :
Czy można przyjąć, że obrót jest statystycznie istotną zmienną kosztotwórczą? (α = 0,05).
Zadanie 8.13
Funkcja regresji wielokrotnej produkcji rolnej (w tys. zł) w 20 gospodarstwach rolnych woj. wielkopolskiego o wielkości powierzchni 20 ha względem powierzchni zasiewu (X1 w ha) i zużycia nawozów (X2 w kg/ha) była następująca:
![]()
; Su = 1,2.
Przyjmując = 0,05 sprawdź, czy powierzchnia zasiewów i zużycie nawozów są istotnymi zmiennymi objaśniającymi.
Zadanie 8.14
Przeprowadzono badanie 19 zakładów produkujących te same wyroby, które dotyczyło wydajności pracy jednego robotnika (Y), ilości zużytej energii na jednego robotnika (X1), oraz płynności kadr (X2). Otrzymano, że:
![]()
, ![]()
, ![]()
.
Sprawdź istotność współczynnika korelacji wielorakiej (α = 0,05),
Zadanie 8.15
Poniższe informacje dotyczą następujących zmiennych :
Y - wydatki miesięczne na żywność w gospodarstwie domowym,
X1 - liczba osób w gospodarstwie domowym,
X2 - dochód miesięczny gospodarstwa domowego.
Przebadano 28 gospodarstw domowych. Wiadomo, że suma iloczynów odchyleń wartości cech Y i X2 od ich średnich arytmetycznych wynosi 1428, natomiast współczynniki korelacji całkowitej wynoszą :
![]()
0,9 ![]()
![]()
0,8.
Zróżnicowanie badanych zmiennych było następujące:
![]()
= 10; ![]()
= 2; ![]()
= 6.
Mając powyższe informacje:
Zadanie 8.16
W przedsiębiorstwie Z zbadano zależność między wydajnością pracy (Y) a stażem pracy (X1) i poziomem wykształcenia (X2) 100 pracowników bezpośrednio produkcyjnych. Wiadomo, że macierz korelacji całkowitej między tymi zmiennymi jest następująca :
P
.
Ustal łączny wpływ stażu pracy i poziomu wykształcenia na wydajność pracy i oceń, czy jest to zależność statystycznie istotna dla = 0,05.
Zadanie 8.17
Na podstawie informacji o kształtowaniu się liczby braków (Y - [szt.]) w zależności od skali produkcji (X1 - [tys. szt.]) oraz stopnia automatyzacji procesu wytwarzania (X2 - [%]), przy produkcji pewnego wyrobu w przedsiębiorstwie Z w latach 1982-1994 oszacowano poniższy model regresji:
![]()
, ![]()
.
Czy obie zmienne objaśniające wpływają w sposób istotny na kształtowanie się liczby braków? Przyjmij = 0,05.
Zadanie 8.18
W jednym z krajów europejskich zbadano zależność między następującymi zmiennymi w latach 1995-2006:
Y - liczba przestępstw na 1000 mieszkańców,
X1 - udział mężczyzn w ludności ogółem,
X2 - procent mężczyzn obcokrajowców wśród całej ludności.
Ustalono, że :
![]()
, ![]()
, ![]()
, ![]()
, ![]()
, ![]()
.
P
Zadanie 8.19
Dana jest macierz korelacji całkowitej P w postaci :
P
.
Przyjmując, że n = 52, sprawdź istotność współczynnika korelacji wielokrotnej. Przyjmij α = 0,10.
Zadanie 8.20
Na podstawie informacji o wartościach trzech zmiennych przedstawionych w tabeli, wyjaśnij:
Lp. |
Spożycie dobra y [kg] |
Cena dobra x1 [zł] |
Cena substytutu x2 [zł] |
1 |
2 |
4 |
2 |
2 |
6 |
4 |
2 |
3 |
8 |
6 |
4 |
4 |
10 |
8 |
6 |
5 |
14 |
8 |
6 |
Źródło: dane umowne.
Zadanie 8.21
Poniższe dane liczbowe dotyczą następujących zmiennych :
Y - wydatki miesięczne na artykuły nieżywnościowe, w przeliczeniu na osobę
w rodzinie,
X1 - liczba osób w rodzinie,
X2 - dochód na osobę w rodzinie,
X3 - wydatki ogółem na osobę w rodzinie.
Wiadomo przy tym, że:
![]()
, ![]()
, ![]()
,
![]()
, ![]()
, ![]()
, ![]()
,
![]()
, ![]()
, ![]()
.
115
Wyszukiwarka
Podobne podstrony:
Podstawy zarządzania wykład rozdział 05
2 Realizacja pracy licencjackiej rozdziałmetodologiczny (1)id 19659 ppt
Ekonomia rozdzial III
rozdzielczosc
kurs html rozdział II
Podstawy zarządzania wykład rozdział 14
7 Rozdzial5 Jak to dziala
Klimatyzacja Rozdzial5
Polityka gospodarcza Polski w pierwszych dekadach XXI wieku W Michna Rozdział XVII
Ir 1 (R 1) 127 142 Rozdział 09
Bulimia rozdział 5; część 2 program
05 rozdzial 04 nzig3du5fdy5tkt5 Nieznany (2)
PEDAGOGIKA SPOŁECZNA Pilch Lepalczyk skrót 3 pierwszych rozdziałów
Instrukcja 07 Symbole oraz parametry zaworów rozdzielających
04 Rozdział 03 Efektywne rozwiązywanie pewnych typów równań różniczkowych
Kurcz Język a myślenie rozdział 12
Ekonomia zerówka rozdział 8 strona 171
28 rozdzial 27 vmxgkzibmm3xcof4 Nieznany (2)
Meyer Stephenie Intruz [rozdział 1]
04 Rozdział 04
więcej podobnych podstron