ESTYMACJA PUNKTOWA

Niech
będzie prostą próbą losową z

rozkładu, którego parametr
jest nieznany.

Definicja. Statystykę
, której realizacje dla konkretnych próbek są „rozsądnymi” ocenami
, nazywamy estymatorem parametru
i oznaczamy

=
.

Definicja. Estymator
parametru jest nieobciążony, jeśli

.

Przykłady.

(a) Średnia z prostej próby losowej jest nieobciążonym estymatorem wartości średniej
.

.

(b) Wariancja z prostej próby losowej jest nieobciążonym estymatorem wariancji rozkładu cechy populacji
.

.

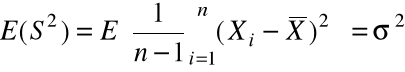
I. Przedziały ufności dla wartości średniej rozkładu normalnego.

Niech
będzie prostą próbą losową z rozkładu normalnego
.

Model 1. ( znane odchylenie standardowe
)

~
.

~
.

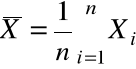
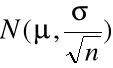
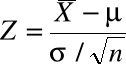
Niech
- ustalona liczba.

=
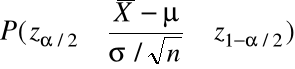
, (1)

gdzie
= kwantyl rzędu
rozkładu
,

= kwantyl rzędu
rozkładu
, tzn.

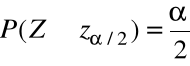
oraz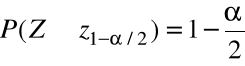
.

Z symetrii standardowej gęstości normalnej

.

Równanie (1) można zapisać jako

=

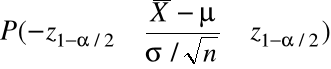
(2)
=

=
.

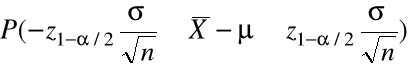
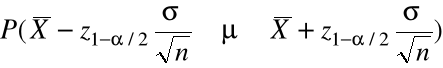
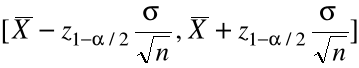
- przedział losowy zawierający z prawdopodobieństwem
nieznaną wartość średnią
. Realizacją tego losowego przedziału obliczoną dla próbki jest

=

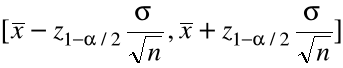
przedział ufności dla
na poziomie ufności

Interpretacja częstościowa (sens praktyczny ) przedziału ufności:

Niech
,
oznaczają średnie próbkowe obliczone dla N próbek:
,
,
. Próbki są realizacjami niezależnych prostych prób losowych (
), (
),...., (
). Dokładniej: wykonujemy N jednakowych niezależnych doświadczeń. Każde k-te ( k = 1,2,...,N ) doświadczenie polega na zaobserwowaniu realizacji k-tej prostej próby losowej (
), tzn. k-tej próbki:
. Przedział ufności dla
na poziomie ufności
obliczony dla k-tej próbki ma postać

.

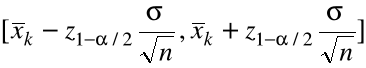
Nieznana nam średnia
nie dla każdej próbki należy do wyznaczonego dla niej przedziału ufności. Ale, niech
oznacza liczbę tych doświadczeń dla których

.

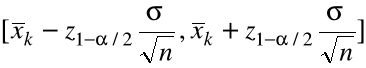
Wówczas na mocy interpretacji częstościowej prawdopodobieństwa zdarzenia, dla
,

=

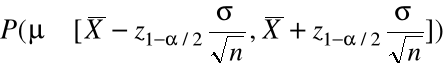
Zatem spośród wielu próbek w przybliżeniu

jest takich dla których wyznaczony przedział ufności zawiera nieznaną wartość średnią
.

Jak duża powinna być liczność próbki n ?

(a) Długość przedziału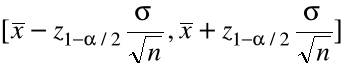

jest stała ( nie zależy od próbki ) równa

.

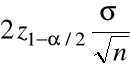
Im większe n tym mniejsza długość przedziału ufności, tzn. tym lepsze oszacowanie przedziałowe
na danym poziomie ufności.

(b) Ze wzoru (2) mamy

=
,

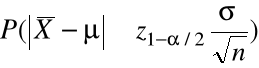
Niech
będzie takie że

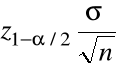
, równoważnie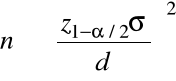
.

Wówczas (wykorzystując
dla
)

=


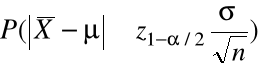
, skąd

.

Udowodniliśmy

Stwierdzenie. Jeśli liczność prostej próby losowej z rozkładu normalnego o wartości średniej
i standardowym odchyleniu
spełnia warunek

,

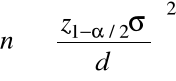
to

.

( Z prawdopodobieństwem co najmniej
błąd bezwzględny oszacowania nieznanej wartości średniej
poprzez
nie przekroczy
, tzn. wśród wielu próbek o liczności n częstość takich dla których błąd bezwzględny średniej próbkowej nie przekroczy d jest w przybliżeniu nie mniejsza niż
. )

Zadanie. Stacja paliw sprzedała 8019 litrów gazu w ciągu 9 losowo wybranych dni. Załóżmy, że dzienna ilość sprzedanego gazu ma rozkład normalny o standardowym odchyleniu
(litrów). Skonstruować przedziały ufności dla średniej dziennej sprzedaży gazu na poziomach ufności:

(a) 0,98 (b) 0,80.

Mamy: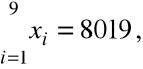
n = 9,
, skąd

1. 
   
   ,
   .

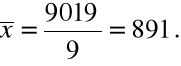
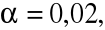
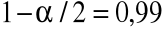
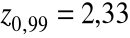
98% przedział ufności dla
:

[891 - 2,33
, 891 + 2,33
] = [821,1, 960,9]

2. 
   ,
   ,
   .

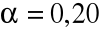
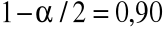
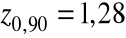
80% przedział ufności dla
= [852,6, 929,4].

Zadanie. Producent chce ocenić średnią zawartość nikotyny w paczkach papierosów pewnego gatunku.

Wiadomo, że standardowe odchylenie zawartości nikotyny w losowo wybranej paczce papierosów
(mg),

Znaleźć liczbę paczek papierosów, w których należy zbadać zawartość nikotyny, aby na poziomie ufności co najmniej 0,95 móc stwierdzić, że obliczona średnia z próbki
nie będzie się różniła od prawdziwej średniej zawartości nikotyny
o więcej niż 1,5 (mg).

Zakładając rozkład normalny zawartości nikotyny w paczce papierosów mamy:

Dla
,

,
.

, jeśli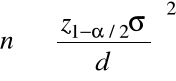
, tzn.

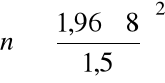
. Stąd liczność próbki powinna być:
.

Model 2. ( nieznane odchylenie standardowe
)

W poprzednim modelu wykorzystano

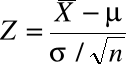
. Podstawiając zamiast
estymator
, tzn.
, gdzie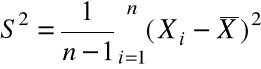
, otrzymujemy zmienną losową

.

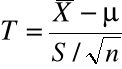
T ma znany rozkład: t Studenta z
stopniami swobody, gdzie

Definicja. Niech
będą niezależnymi zmiennymi losowymi o rozkładach
.

Rozkład prawdopodobieństwa zmiennej losowej

=
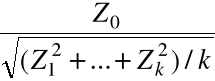
nazywamy rozkładem t Studenta z k stopniami swobody.

Notacja.
.

Własności rozkładu
:

Gęstość symetryczna o podobnym kształcie jak gęstość normalna,
Dla
można przyjąć

.

Mając zmienną losową
budujemy przedział ufności dla
analogicznie jak w modelu 1:

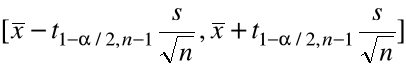
, gdzie

= kwantyl rzędu
rozkładu t Studenta o
stopniach swobody.

Uwaga. Jeśli
, to przyjmujemy

.

Zadanie. Zanotowano czasy obsługi przy okienku kasowym ( w minutach ) 64 losowo wybranych klientów pewnego banku. Obliczono: średnią z próbki
(min.) oraz wariancję z próbki
(min.
)

Znaleźć 98% przedział ufności dla średniego czasu obsługi
, jeśli można założyć, że czas obsługi klienta przy okienku kasowym ma rozkład normalny.

Mamy:
,
, n =64,
= liczba stopni swobody,
,
,

.

98% przedział ufności dla
ma postać

=

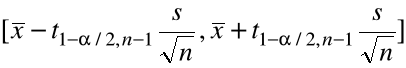
[3,2 - 2,33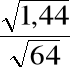
, 3,2 + 2,33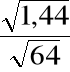
] = [2,85, 3,55].

Zadanie. W ciągu pięciu losowo wybranych tygodni zaobserwowano następujące zużycia cukru ( w gospodarstwie domowym, w kg ):

3,8, 4,5, 5,2, 4,0, 5,5.

Skonstruować 90% przedział ufności dla średniego tygodniowego zużycia cukru w tym gospodarstwie, jeśli

można przyjąć rozkład normalny zużycia cukru.

Obliczamy:
= 4,6 oraz

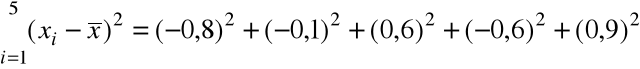
= 2,18.

Stąd,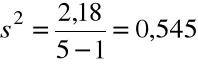
,
= 0,738

,
, 5 - 1 = 4 = liczba stopni swobody,
2,132.

90% przedział ufności dla
ma postać:

=

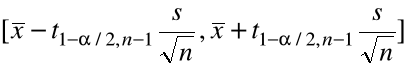
[ 4,6 - 2,132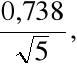
4,6 + 2,132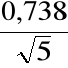
]= [3,896, 5,304].

II. Przedziały ufności dla różnicy wartości średnich dwóch rozkładów normalnych.

Niech
oraz
będą dwiema niezależnymi prostymi próbami losowymi z rozkładów normalnych
oraz
, odpowiednio.

Model 3. ( znane odchylenia standardowe
)

Średnie z obu prób losowych
są niezależnymi zmiennymi losowymi o rozkładach normalnych

,
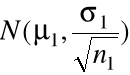
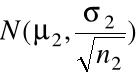
, odpowiednio. Stąd z własności rozkładu normalnego
ma rozkład normalny o wartości średniej
i wariancji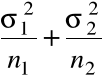
, gdyż

E(
) = E(
) + E( -
) = E(
) - E(
)

Var(
) = Var(
) + Var(-
) =

Var(
) +
Var(
) =
,

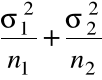
skąd po standaryzacji mamy

~
.

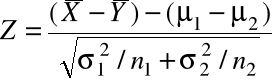
Postępując dokładnie tak samo jak w przypadku jednej próby (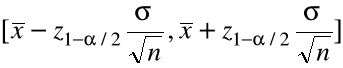
)otrzymamy przedział ufności dla
na poziomie ufności
:

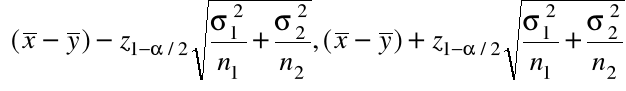
Model 4. ( nieznane odchylenia standardowe
)

Założenie dodatkowe:
,
- nieznane.

=

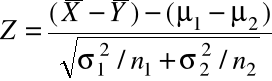
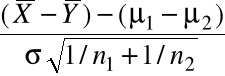
Var(
) =
,

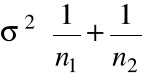
Niech

,
-

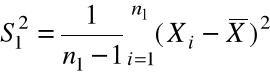
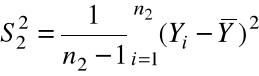
nieobciążone estymatory
.

Estymatorem nieobciążonym
, opartym na dwu próbach łącznie, jest statystyka

.

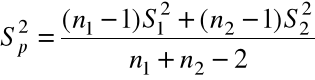
Wówczas we wzorze na Z podstawiając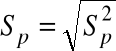

zamiast
otrzymujemy statystykę

~
.

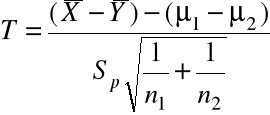
Analogicznie jak w modelu 3 otrzymujemy przedział ufności dla
na poziomie ufności
:

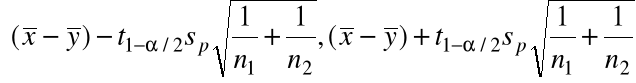
gdzie:

= kwantyl rzędu
rozkładu t Studenta z
stopniami swobody.

Zadanie. 10 żarówek producenta A miało średni czas życia 1850 (godz.) oraz standardowe odchylenie
(godz.). Natomiast 12 żarówek producenta B miało średni czas życia 1940 (godz.) oraz standardowe odchylenie
(godz.). Skonstruować 95% przedział ufności dla różnicy prawdziwych wartości średnich czasów życia żarówek producentów A i B.

( podać odpowiednie założenia ).

Zadanie. U 8 kierowców zanotowano czasy reakcji ( na pewien bodziec ) w sek. :

3,0, 2,0, 1,0, 2,5, 1,5, 4,0, 1,0, 2,0.

U 6 innych kierowców zbadano czasy reakcji n bodziec po spożyciu określonej dawki alkoholu:

5,0, 4,0, 3,0, 4,5, 2,0, 2,5.

Znaleźć 95% przedział ufności dla różnicy wartości średnich czasów reakcji w obu populacjach.

Zadanie. Dla realizacji 2 niezależnych prób losowych z rozkładów normalnych otrzymano:

,
,

,

,

Znaleźć 90% przedział ufności dla różnicy wartości średnich tych rozkładów.

=
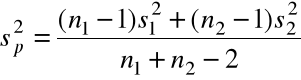
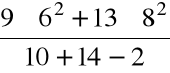
= 52,55.

,
=

liczba stopni swobody,

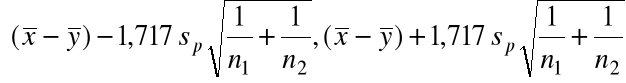
[50 - 56 - 1,717(7,249)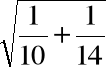
, 50 - 56 +

1,717(7,249)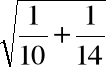
] = [-11,15, -0,85].

III. Przedziały ufności dla wariancji rozkładu normalnego.

Model 5. Przedział ufności dla wariancji.

Niech
będzie prostą próbą losową z rozkładu normalnego
,
są nieznane.

Definicja. Niech
będą niezależnymi zmiennymi losowymi o rozkładach
. Wówczas zmienna losowa

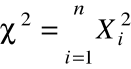
ma rozkład
o n stopniach swobody.

Notacja:
.

Zauważmy, że dla prostej próby losowej z rozkładu
, po standaryzacji, zmienne losowe

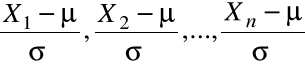
są niezależne o rozkładach

. Stąd

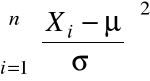
Dowodzi się, że zastępując nieznaną wartość średnią
przez średnią z próby losowej
otrzymamy zmienną losową:

.

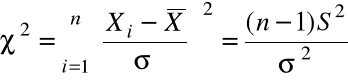
Stąd

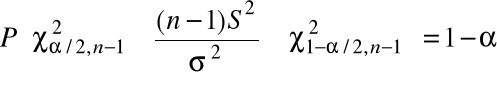
, (3)

gdzie
,
są kwantylami rzędu
,
, odpowiednio, rozkładu
.

Wzór (3) zapisujemy równoważnie:

.

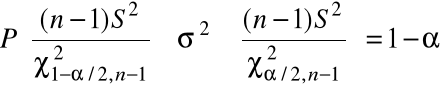
Stąd, przedziałami ufności na poziomie ufności
są

(a) dla wariancji
rozkładu normalnego

,

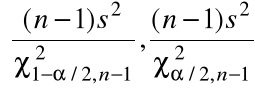
(b) dla standardowego odchylenia
rozkładu normalnego

.

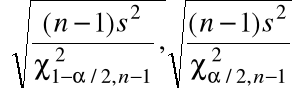
Zadanie. Plastyk zużył następujące ilości farby do pomalowania 6 talerzy:

8,1, 8,7, 7,6, 7,8, 8,5, 7,9.

Znaleźć 95% przedział ufności dla wariancji, zakładając

rozkład normalny farby potrzebnej do pomalowania 1 talerza.

Rozwiązanie.

Obliczamy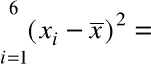
0,9. Stąd

=
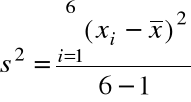
= 0,18.

= 0,025,
= 0,975,
= liczba stopni swobody.

Z tablic kwantyli rozkładu
można odczytać

,

=

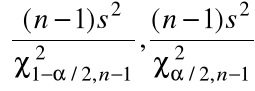
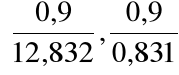
Model 6. Przedział ufności dla ilorazu wariancji dwóch rozkładów normalnych.

Niech
oraz
będą dwiema niezależnymi prostymi próbami losowymi z rozkładów normalnych
oraz
, odpowiednio.

Wówczas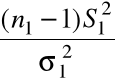
,
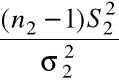
są niezależnymi zmiennymi losowymi, o rozkładach
o
,
stopniach swobody, odpowiednio.

Definicja. Niech U, V będą niezależnymi zmiennymi losowymi oraz

. Wówczas rozkład prawdopodobieństwa zmiennej

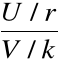
nazywamy rozkładem F Snedecora z r i k stopniami swobody.

=

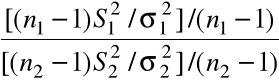
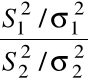
Zatem zmienna losowa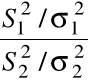
ma rozkład F Snedecora z
,
stopniami swobody.

=
,

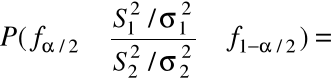
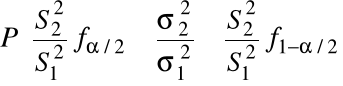
gdzie
są kwantylami rzędu
, odpowiednio, rozkładu F Snedecora z
,

stopniami swobody.

Wiadomo, że
. Zatem przedział ufności dla ilorazu wariancji
na poziomie ufności
ma postać

.

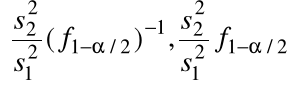
IV. Przedziały ufności dla proporcji.

Model 7. Niech
będzie prostą próbą losową z rozkładu Bernoulli'ego o nieznanym parametrze p.

Wówczas
,
.

Niech
=
. Z centralnego twierdzenia granicznego

dla dostatecznie dużego n zmienna losowa

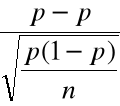
ma rozkład bliski rozkładowi

( musi zachodzić
).

Można też udowodnić, że zmienna losowa

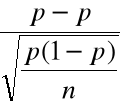
ma rozkład bliski
, o ile
.

Stąd

.

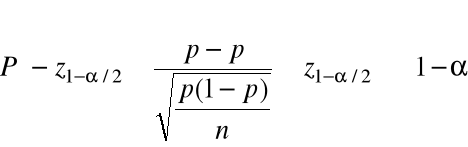
Równoważnie

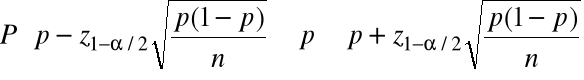
Przedział ufności dla p na poziomie ufności
jest realizacją przedziału losowego:

.

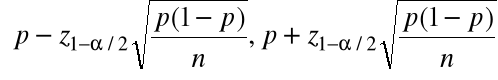
Przykład. W badaniach opinii publicznej otrzymano wynik: 57% spośród 1000 ankietowanych Polaków poparło wejście Polski do Unii Europejskiej, a pozostałych 43% osób było przeciwnych. Skonstruować 95% przedział ufności dla proporcji p obywateli popierających wejście Polski do UE.

Mamy:

= 0,57,
= 0,95,
,

= 1 - 0,025 =0,975. Z tablic:
= 1,96.

Próba jest bardzo liczna oraz spełnione są warunki

,
.

Zatem można wykorzystać powyżej znaleziony przybliżony przedział ufności:

=

=

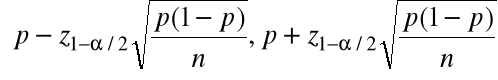
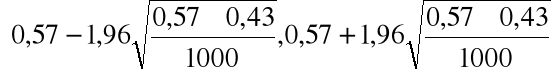
= [0,54, 0,60].

Zatem mamy „95% pewności”, że proporcja Polaków popierających wejście Polski do UE jest liczbą z przedziału [0,54, 0,60].

Zadanie. Spośród 400 dorosłych przypadkowo wybranych osób zapytanych o regularne uprawianie sportu rekreacyjnego 160 osób odpowiedziało twierdząco. Skonstruować 98% przedział ufności dla

p = proporcji osób uprawiających sport rekreacyjny w danej populacji.

Mamy: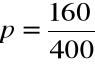
= 0,4, n = 400,
,
,
.

,

=

=

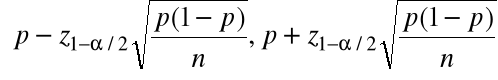
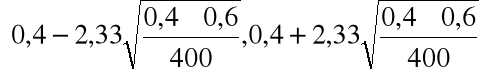
= [0,343, 0,457] = 98% przedział ufności dla p.

---