015 (9)

Równania harmonicznego pola elektromagnetycznego -fale elektromagnetyczne

B = rot A

potencjały elektrodynamiczne

E = -grad V - jcoA

I0C=>

rot rot A = -jap {;/+ jcoe) A - p (y+ jooe) grad V+//J_iVV//; div Ą = -fi(y + j(OE) V    k -yjjap(ja jcoe)

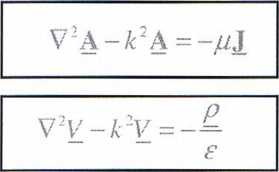
Równanie Helmholtz’a

Równanie Helmholtz’a

Równania pola elektromagnetycznego harmonicznego -fale elektromagnetyczne

v²a

w

i a²A

v

² ar

i d²v

v² a t²

jui

Ł

s

niejednorodne równania falowe

dla pól zmieniających się sinusoidalnie w czasie po wprowadzeniu wielkości zespolonych l_wym=J_h,_yme’⁹’, A=A V= V e><p równania przyjmą postać _

Y²A-£^:A = -ul

równania Helmholtz’a

YV — h^2V —	_£
	e