Image0080 BMP

9. HARMONICZNE POLE ELEKTROMAGNETYCZNE W ŚRODOWISKU PRZEWODZĄCYM

9.1. Równania pola elektromagnetycznego w środowisku przewodzącym

W niniejszym rozdziale rozpatrywać będziemy harmoniczne pola elektromagnetyczne o niezbyt dużej częstotliwości, istniejące w środowiskach przewodzących. W tych warunkach dopuszczalne staje się pominięcie prądów przesunięcia, wobec czego — zgodnie z wywodami w p. 8.2 — stosować będziemy równania Maxwella w postaci zespolonej:

rotH = yE,

rotE = — jcojuH,

(9.1)

(9.2)

gdzie: y, /1 oznaczają odpowiednio konduktywność i przenikalność magnetyczną środowiska przewodzącego. W dalszych rozważaniach będziemy przyjmować, że wielkości te są stałe. Norma wektorów zespolonych charakteryzujących pole elektromagnetyczne jest zawsze równa wartości skutecznej odpowiedniego wektora (por. p, 8.1.2).

Potencjał wektorowy harmonicznego pola elektromagnetycznego spełnia niejednorodne równanie Helmhoitza (por. p. 8.4)

V²A —k²A=—/iJ,,

(9.3)

gdzie: J_M oznacza gęstość prądu narzuconego, zaś

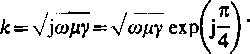
(9.4)

Potencjał skalarny pola wyraża się wzorem

1

K=--djvA.

Natężenie pola elektrycznego jest równe

E=E, + E_tt.,,

(9.5)

(9.6)

przy czym

przedstawiają odpowiednio natężenie indukowanego i statycznego pola elektrycznego (por. p. 8.4). W rozpatrywanych w tym rozdziale zagadnieniach zawsze div A-O w obszarze środowiska prze wodzące go, wobec czego E=0 w tym obszarze. W tych warunkach natężenie pola elektrycznego E równa się natężeniu E₍ indukowanego pola elektrycznego.

Natężenie pola magnetycznego wyraża się wzorem

rot H = — rot A,    (9.8)

— fi

/godnie z zależnością (8.35).

9.2. Zjawisko naskórkowości w przewodzie walcowym

9.2.1. Uwagi ogólne

Rozkład prądu zmiennego w przewodzie jest nierównomierny, W prz.ypadku przewodu walcowego największa gęstość występuje przy powierzchni przewodu, a najmniejsza — wzdłuż jego osi. Nierównomierność rozkładu powiększa się w miarę wzrostu częstotliwości, a przy bardzo dużych częstotliwościach prąd płynie praktycznie w cienkiej war-\twie przewodu przy jego powierzchni. Z tego powodu zjawisko to nosi nazwę naskórkowości.

Zjawisko naskórkowości wywołuje zmianę iinpcdancji wewnętrznej przewodu. Ze wzrostem częstotliwości zwiększa się rezystancja przewodu, a jego indukcyjność wewnę-tr/n:i maleje.

Zbadamy zjawisko naskórkowości występujące przy przepływie prądu sinusoidalnego w przewodzie walcowym.

9.2.2. Pole elektromagnetyczne we wnętrzu przewodu walcowego

W bardzo długim przewodzie metalowym o przekroju kołowym płynie prąd sinusoidalny o wartości zespolonej /. Przyjmujemy, że przewód jest prostoliniowy i pominiemy wpływ drugiego przewodu, którym prąd wraca do źródła. Niech y, ft oznaczają kondu-l.ivwność i przenikalność magnetyczną przewodu.

Wprowadzimy współrzędne walcowe z, 0, z w ten sposób, że Or jest osią przewodu, (ięstość prądu J oraz natężenie pola elektrycznego E są równoległe do osi przewodu, u więc mają tylko składowe J_z oraz E_z. Ze względu na symetrię układu, składowe J_t maz E. zależą wyłącznie od współrzędnej r.

Obliczając rotację wektora E, widzimy na podstawie wzoru (9.2), że natężenie pola marne!ycznego ma tylko składową H_t) zależną od współrzędnej r, przy czym

//«-

1 df_;

jojfi dr

(9,9)