Image0029 BMP

pui, ./mu - r- r_k, |. Wyk ir. natężenia pola elekt ryt/nogo wzdłuż. promienia w kon-.l.u..ii,.t/i tni|w..[siwimym przedstawia rys. 2.IK dla przypadku r,,=3, I, i:_r, -2. Nie. nii.li>.. natężenia pola elektrycznego w punktach powierzchni granicznych wynika / i.mtt.itii.t (i7).

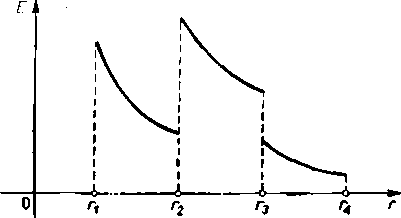
Rys. 2.18. Wykres natężenia pola elektrycznego między okładkami trój warstwowego kondensatora walcowego

2.7. Pojemność linii elektrycznych 2.7.1, Pojemność pojedynczego przewodu nad ziemią

Bardzo długi przewód o promieniu z,, umieszczony jest na wysokości /; nud powierzchnią ziemi (rys, 2.19). Na tym przewodzie znajduje się ładunek o stałej gęstości liniowej r Przyjmujemy, ż.c potencjał w punktach powierzchni ziemi równy jest zeru. W celu zrealizowania tego warunku rozpatrzymy dwa ładunki liniowe przeciwnego znaku, umieszczone w nieograniczonym środowisku o przen i kalii ości elektrycznej i;„ wzdłuż dwóch

+ T

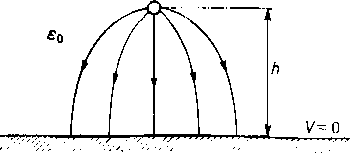
Rys. 2.10. Przewód naładowany nad powierzchnią ziemi

linii równoległych, oddalonych od siebie o 2/i (rys. 2.20). Potencja! w punkcie P pula wyznaczamy za pomocą metody superpozycji, otrzymując

r i	- r	, <
In	+	In
'm:0 r	i 2;n;(1

r,

In *

(2.75)

zgodnie z zależnością (2.46). W |iuii^:lai!i j-ł.¹ .z_L/y/ny symetralncj (r,    m), odpowiada

jącej po wict/clmi ziemi, mamy t—o, wobec czego pole elekttyczne mul tsi płaszczyzną jest takie samo jak w układzie rzeczywistym nad powierzchni;} ziemi.

Rzeczywisty układ z rys. 2.19 zastąpiliśmy układem równoważnym / rys. 2.20, stosując Izw. metodę odbić zwierciadlanych. Ładunek liniowy — r na rys. 2.20 nazywa się odbiciem zwierciadlanym ładunku +r względem powierzchni ziemi.

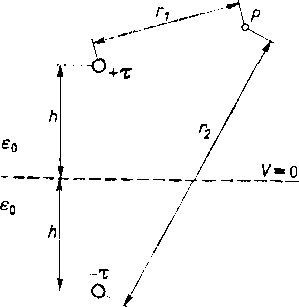
Rys. 2.20. Ładunek liniowy i jego odbicie zwierciadlane w nieograniczonym środowisku

Załóżmy, że każdy ładunek liniowy z rys. 2.20 odpowiada przewodowi o promieniu W celu wyznaczenia potencjału górnego przewodu przyjmiemy, że punkt P znajduje sic na jego powierzchni. Wówczas r, =r₀ oraz r, t 2/i, co jest słuszne dla i\,    2h\ wobec

tego potencjał górnego przewodu

r

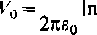
2/i

>'o

(2-76 >

zgodnie ze wzorem (2.75). Jest rzeczą oczywistą, że otrzymany wzór przedstawia również potencjał przewodu z rys, 2.19,

Układ z rys. 2.19 można traktować jako kondensator, którego jedną Okładką jes-powicrzchnia przewodu, a drugą okładką — powierzchnia ziemi, Pojemność tego koni densalora na jednostkę długości, czyli pojemność jednostkowa wyraża się wzorem

C’ =

2ite₀

2h

In

ło

(2.77)

uli/¹- manym przy wy k orzy s tan i u zal eżn ości (2.76). W zor te n przed stawi a pojemność g ilu■•stkouą przewodu nad powierzchnią ziemi, a jednostką jej jest larad na metr (lym). Pojemiiość odcinka przewodu o długości / wynosi

C--CI

2Ttr„ /

2 h In

(2.7M