Image0102 BMP

mu wymiat opom > nazywa su,- http. ii,ut<ją falową dielektryka. łrnpcduncję lalową dielektryka o względnych przeniknlnnściach: elektrycznej c_r oraz magnetycznej //, można przedstaw ić w postaci w/oru liczbowego

(10. JH)

Z^/rOrr /-^    [O].

\ ^

Impedancja falowa próżni wynosi zatem

Z_f =120a - 377 fi.

Iloraz wartości chwilowych (10.14) jest równy impedancji falowej dielektryka, czyli

^E‘ _

a stąd otrzymujemy

(10.19)

H, V e ’

{cEt^\pU;,

Wynika stąd, że w dowolnej chwili gęstości energii pola elektrycznego i pola magnetycznego są jednakowe w każdym punkcie strefy falowej, czyli w jednostce objętości zawarta jest taka sama energia pola elektrycznego jak i pola magnetycznego. Oznacza to, że połowa energii fali zawarta jest w polu elektrycznym, a druga połowa — w polu magnetycznym, 10.2.4. Moc i rezystancja promieniowania

Zespolony wektor Poyntinga w strefie falowej jest równy

tyli* = £•„#*!,,    (10.20)

owiem 1 o >' 1 _v = 1,. Wektor Poyntinga ma zatem kierunek radialny, wobec czego \vy-tępuje przepływ mocy w kierunku radialnym. Jest to oczywiste z fizycznego punktu wi-zenia, bowiem istniejąca w badanym układzie fala kulista unosi energię. Podstawiając ileiności (10,12) i (10.13) do wzoru (10.20), otrzymujemy

(i 0.21)

zy uwzględnieniu, że k wyraża się liczbą urojoną.

Rozpatrzmy kulę o promieniu r w strefie falowej wibratora elementarnego, znajdują-go się w środku tej kuli (rys. 10,2), Moc wypromieniowana przez powierzchnię S oma-anej kuli równa jest strumieniowi mocy, czyli strumieniowi zespolonego wektora Poynt-lii przez tę powierzchnię i nazywa się mocą promieniowania wibratora. W celu oblicze-i tej mocy podzielimy powierzchnię kuli aa elementy o postaci pasów o szerokości '), przy czym pole powierzchni takiego pasa jest równe 2ar² sin (MO. Moc prorruenio-nin jest zatem równa

sili³ 0d0,

P„- <£[ExH>] dS-

J    16it (ue r

s    o

o

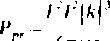
6rco>E

(10.22)

Na podstawie otrzymanego wzoru stwierdzamy, że moc promieniowania wibratora pi/ybicra wartości rzeczywiste i nie zależy od odległości od wibratora. Niezależność od odległości jest skutkiem przyjętych założeń, bowiem strumień mocy unoszony przez falę

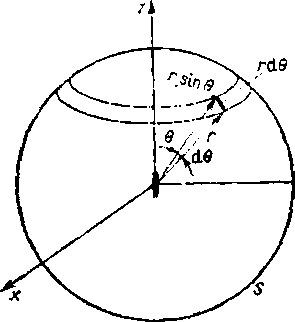
Rys. 10.2. Kula w strefie falowej wibratora elementarnego

y

i ozprzestrzen tającą się w idealnym dielektryku nic ulega żadnym stratom. Moc promieniowania jest zatem wielkością charakteryzującą zdolność wypromieniowania mocy przez wibrator. Przy wykorzystaniu zależności (10.2) oraz (10.4), wzór (10.22) dla mocy promieniowania wibratora można przedstawić w postaci

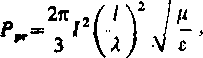
(10.23)

gdzie ). oznacza długość fali Jelekt roni agne tycznej, czyli

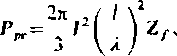
(10.24)

zgodnie ze wzorem (10.17), przy czyni 7_f jest impedancją falową dielektryka. Wynika stąd, że moc promieniowania wibratora jest odwrotnie proporcjonalna do kwadratu długości fali elektromagnetycznej. Oznacza to, że wypromieniowanie mocy przez wibrator jest intensywne przy małych długościach fal, czyli przy dużych częstotliwościach,

Podstawiając wyrażenie (10.18) do zależności (10.24), otrzymuje się wzór liczbowy określający moc promieniowania wibratora

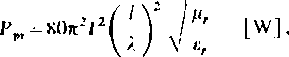
(10.25)

<W\K