Image0026 BMP

2.6. Pojemność elektryczna. Kondensatory 2.6.1. Określenie pojemności

Kondensatorem nazywamy układ dwóch ciał metalowych nazywanych elektrodami (okładkami), które oddzielone są dielektrykiem. Gdy między okładkami kondensatora istnieje napięcie, wówczas na powierzchni okładek kondensatora zgromadzone są ładunki przeciwnego znaku, równe co do wartości bezwzględnej. Kondensator jest zatem urządzeniem służącym do magazynowania ładunku elektrycznego.

Pojemnością C kondensatora nazywamy iloraz ładunku q na jednej okładce przez napięcie u między okładkami, czyli (2.59)

u

Gdy dielektryk między okładkami jest liniowy, wówczas pojemność kondensatora jest wielkością stałą, zależną od wymiarów geometrycznych ukiadu. Jednostką pojemności jest 1'arad (F).

Pojemnością C odosobnionego ciała metalowego nazywamy iloraz ładunku q tego ciała przez jego potencjał V₀, czyli

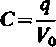
(2-60)

Na przykład pojemność odosobnionej kuli metalowej o promieniu r₀, umieszczonej w środowisku o stałej przenika! ności elektrycznej o, równa się

(2.61)

C*=4nsr_g,

zgodnie ze wzorem (2.40).

Kondensatory można łączyć równolegle lub szeregowo. Pojemność zastępcza połączenia równoległego kondensatorów równa się sumie pojemności kondensatorów tworzącycli połączenie. Odwrotność pojemności połączenia szeregowego kondensatorów równa się sumie odwrotności pojemności kondensatorów zawartych w połączeniu.

2.6.2. Kondensator płaski

Kondensator płaski ma dwie jednakowe okładki umieszczone równolegle na przeciw siebie (rys. 2.12). Między okładkami kondensatora znajduje się dielektryk o przenikalności elektrycznej c. Gdy wymiary poprzeczne okładki kondensatora są bardzo duże w porównaniu z odległością d okładek, wówczas przy pominięciu zniekształceń pola blisko brzegów płytek można przyjąć, że pole jest równomierne w obszarze między okładkami kondensatora.

Niech E, D oznaczają natężenie pola elektrycznego oraz indukcję elektryczną w dowolnym punkcie pola równomiernego między okładkami kondensatora. Napięcie między okładkami kondensatora płaskiego jest równe u = Ed, wobec czego natężenie pola elektrycznego

E —

u

d

(2.62)

W obszai/c między okładkami kondensat* >i u intuicje strumień elektryczny </-•/j,\ j_)r/y czym <1 jest ładunkiem znajdującym się mi jednej płytce, a ,9 - polem powierzchni jednej

płytki. Indukcja elektryczna w dowolnym punkcie obszaru między płytkami jest równa

u

D = £ E = £    ,

d

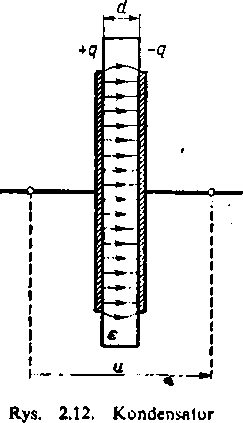
płaski

wobec czego

eSu

Pojemność kondensatora płaskiego wynosi zatem

(2.63)

ą cS u d

2.6.3. Uwarstwiony kondensator plaski

Między okładkami uwarstwionego kondensatora płaskiego istnieją trzy warstwy dielektryków o przenika!nościach elektrycznych    £₃ (rys. 2.13). Gdy odległość rf, +

■+■ d₂ + t/j płytek jest nieznaczna w porównaniu z rozmiarami płytek, wówczas możemy przyjąć, żc w obszarze między płytkami pole jest równomierne. Powierzchnia graniczna dwóch dielektryków jest powierzchnią ekwipoteucjalną. W związku z tym układ /. rys. 2.13 można przedstawić w postaci połączenia szeregowego trzech kondensatorów, pr/.y czym w obszarze między płytkami każdego kondensatora znajduje się dielektryk o lalej przen i k a I n ości cle k trycznej.