Image0107 BMP

1.2. Metoda rozdzielenia zmiennych .2.1. Określenia i zależności podstawowe

Przedmiotem dalszych rozważań będą równania różniczkowe cząstkowe, w których siennymi niezależnymi są wyłącznie współrzędne punktu pola. Przykładami takich wnań są równania: Laplace'a, Poissena i Hclmholtza.

Przy stosowaniu me lody rozdzielenia zmiennych, zwaną również metodą Fouriera, zed stawia się rozwiązanie równania różniczkowego cząstkowego w postaci wielokrot-go szeregu nieskończonego

OCJ

u (x, y, z) = Y. ^An«,t *»(*) yjy)Zj(z) ■

(U.3)

yrazy X„(x) >„0') 7._k(z) tego szeregu spełniają dane równanie różniczkowe cząstkowe lazywają się funkcjami własnymi, natomiast A„„_Ik jest stalą. W przypadku zagadnienia mwymiarowego funkcje it przedstawia się v. postaci szeregu podwójnego

(M.4)

Ciąg funkcyjny    którego elementy A',,(x) są całkowalne z kwadratem w prze-

lale (a, b), jest ciągiem ortogonalnym w tym przedziale, jeżeli zie /4>0 jest wielkością stalą. Ciąg funkcyjny ,Y„(v) jest ciągiem ortogonalnym unor-iwanym, gdy A= I w wyrażeniu (11.5).

Normą ciągu funkcyjnego    nazywamy wyrażenie

(11.6)

f X²B(x)dx.

Przypuśćmy, że funkcja f{x) jest całkowalna z kwadratem w przedziale {a. b) oraz iłnia w tym przedziale warunki Dirichleta, które głoszą, żc

1)    przedział (a, b) można podzielić na skończoną liczbę takich części, w których funk-^! f{x) jest nionotonieznu,

2)    funkcja y(jr) ma w przedziale (zr, b) skończoną liczbę punktów nieciągłości, a po-

tlto jej wartość bezwzględna jest ograniczona w każdym punkcie tego przedziału, nteję f{x) można wówczas przedstawić w postaci uogólnionego szeregu Fouriera wzglę-m ortogonalnego ciągu funkcyjnego    a mianowicie

(11.7)

o— 1

b

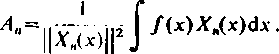
/(*>= X A *„(*),

I.S: 1

Ul-8)

Ciąg funkcyjny j V„( v)} jcsl orhuion.ilm : wogg i>(\) w pr/cd/inlr (u./>l, jeMi

\x_n(x)X_n,(x)wix)dxJ_[°_A ^

gd/ie: A > O jest wielkością stałą; zazwyczaj zakłada się, że w(.r)> 0. Normę ciągu funkcyjnego {A„(.v)} ortogonalnego z wagą u(x) określa wzór

I *

||*<j(*)|| = J ^.²(x)w(x)dx.

Y d

Uogólniony szereg Fouriera funkcji f(x) względem ortogonalnego ciągu funkcyjnego |A'„(x)} z wagą w (a) wyraża się wzorem (11.7), w którym A„ oblicza się ze wzoru

jjW„(x)|p.

/(x)X„(x)w?(x)dx,

gdzie normę ||A'„(x)]| przedstawia zależność (11.10). Powyższe wyrażenia są prawdziwe przy założeniu, że funkcja /(a) jest całkowalna z. kwadratem w przedziale (a, b) i spełnia warunki Dirichlcia w tym przedziale.

Rozpatrzmy funkcję j(x, j) dwóch zmiennych x, y określoną i całkowalną z kwadratem w obszarze S. Niech (At(a)} oraz {K_m(y)} oznaczają ortogonalne ciągi funkcyjne określone odpowiednio dla każdego x oraz y z omawianego obszaru. Uogólnionym podwójnym szeregiem funkcji /(x, y) względem ciągów ortogonalnych |Y_ł(x)} oraz {F_m(y)| nazywamy wyrażenie

/(*>)’) = Z •'libi.^,,r<n(-^v• A’)’    (M.12)

*, »i “ i

gdzie:

v_km(x, y) =- A\(a) Yj y)    (11.13)

jest funkcją własną, zaś A_km jest wielkością stalą.

Normę funkcji własnej przedstawia wzór

, yjdTdy.    (11.14)

Współczynniki uogólnionego szeregu Fouriera oblicza się ze wzoru

(11.15)

■ j-^ |,, J |f(x, y)(*,„(a . v)dxdy.

(II. 16)

(11.17)

Normę funkcji własnej ortogonalnej z wagami h,( v). ir,(r) przedstawia wzór !|t't,n|i ' Ij , y) W,(a ) w₂(y)dxdy, a współczynniki uogólnionego szeregu Fouriera wyrażają się wzorem A_hm = |, .,. J]'/(-’£ ■ )’) v_km( x, y) w, ( a ) w ,(y) d a dy.