Image0073 BMP

8. HARMONICZNE POLE ELEKTROMAGNETYCZNE

8.1.    Wektory zespolone

8.1.1.    Określenie wektora zespolonego

Pole elektromagnetyczne nazywamy harmonicznym, gdy wektory charakteryzujące to pole są wielkościami sinusoidalnie zmiennymi w czasie. Harmoniczne pole nazywane jest często polem sinusoidalnym. Składowe sinusoidalnie zmiennego w czasie wektora W, w układzie współrzędnych prostokątnych wynoszą:

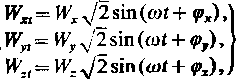
(8.1)

gdziei W_x, W_y, W_z oznaczają wartości skuteczne odpowiednich składowych, <p_x, q>y, ę_L — ich fazy, zaś w jest pulsacją.

Podane oznaczenie wartości skutecznych składowych wektora stosowane będzie w dalszej części skryptu dotyczącej pól harmonicznych, zaś wartości chwilowe wektorów lub jego składowych oznaczać będziemy za pomocą indeksu

Wartości zespolone składowych rozpatrywanego wektora wyrażają się wzorami:

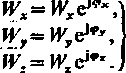
(8.2)

Wartości chwilowe składowych wektora W, oblicza się przy znanych wartościach zespolonych na podstawie wzorów:

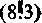
W_xt = \m[_W_x^2^;

a wartość chwilową wektora z zależności

Wcktonin zespolonym W nazywamy wektor, którego składowymi nq wartości zespolone składowych wektora sinusoidalnie zmiennego w czasie, czyli

(8.5)

Wartość chwilową W, wektora przedstawia zatem W2Ór

W,=lm[W72e^i<ut].    (8.6)

Składowe wektora zespolonego są liczbami zespolonymi.

Wprowadzenie pojęcia wektora zespolonego ułatwia analizę harmonicznych pól elektromagnetycznych, podobnie jak wprowadzenie wartości zespolonych prądów i napięć ułatwia analizę obwodów prądu sinusoidalnego. Wektory zespolone stosuje się równic! w innych układach współrzędnych, a więc w układzie współrzędnych walcowych, kulistych ,

]|p.

8.1.2. Norma wektora zespolonego

W celu otrzymania wielkości nieujemnych charakteryzującej wartość liczbową (miarę) wektora zespolonego wprowadzamy pojęcie normy. Normą wektora zespolonego nazywamy wyrażenie

|jW|| = 7\V-W*,    (8.7)

gdzie:

W* = 1, W^+1, W*^+1 _tW*₂    (8.8    i

iesi sprzężonym wektorem zespolonym, którego składowe są liczbami zespolonymi sprzężonymi ze składowymi wektora zespolonego W. We wzorze (8.7) kropka oznacza iloczyn •kaiarny wektorów. Pojęcie normy stosowane jest w teorii liniowych przestrzeni wek-i orowych.

Podstawiając wyrażenia (8.5) i (8.8) do wzoru (8.7), otrzymujemy    *

|| Wjj    W* + W_yW* + W_z wj,

/godnie z określeniem iloczynu skalarnego, wobec czego

||w||=V«^+if;²+H;².    (8.9)

bowiem iloczyn liczb zespolonych sprzężonych jest równy kwadratowi modułu tej liczbV-Stw ierdzamy, że norma wektora zespolonego jest równa pierwiastkowi sumy kwadratów wari ości skutecznych składowych wektora, czyli pierwiastkowi sumy kwadratów moduł .v składowych wektora zespolonego. Ze wzoru (8.9) wynika, że norma wektora jest liczbą rzeczywistą nieujemną.

Obliczymy wartość skuteczną wektora W, sinusoidalnie zmiennego w czasie. Kwadrat tej wartości skutecznej jest równy średniej wartości za okres kwadratu wartości chwilowej,

c/yli

TT    T

[ K,²dr= ~ J W, • W,di = | J (K¹, + w;_r + wl)dt.

U    o    0