Image0011 BMP

wcktoia A w/dluż kt/ywcj ( prze/ pole lej powierzchni, gdy tn pole dąży do /era, czyli

$ A-dl

rot„A=lim^C •    (1.27)

ĄS^O AA

Określenie rotacji nie zależy od układu współrzędnych, jednakże posiać wzoru dla rot A zależy od przyjętego układu współrzędnych.

Obliczmy składowe rotacji w układzie współrzędnych prostokątnych. Rozpatrzmy prostokąt o bokach równoległych do osi Oy oraz Oz (rys. 1.8). Całka liniowa wektora

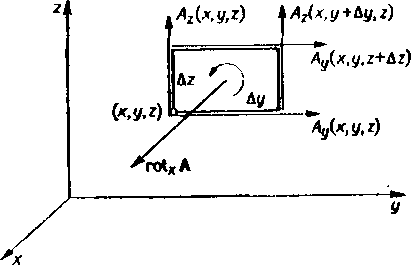
Rys. 1.8. Powierzchnia elementarna w polu wektorowym

A wzdłuż obwodu rozpatrywanego prostokąta jest równa

[A(x, y + Ay, z)-A_z(x, y, z)] Az-[_A^x_t y, z + AzJ-zł/jc, y, z)]Ay =

oA_z

= ■    Ay Az -    Az Ay,

dy    ^tdz

zgodnie ze wzorem Taylora. Pole rozpatrywanego prostokąta wynosi AyAr, wobec czego na podstawie wzoru (1-27), otrzymujemy

. SA. SA

rot, A=— ---■

dy Sz

W podobny sposób znajduje się

dA_x SA_t ^ro,’^A= & " & ■

ox Oy

n rotację wektora A przedstawiamy w postaci

(I.28)

\dy di) • \Si 6x) ’ \Bx dy) ‘

W/ory dla rotacji wektora w innych układach współrzędnych podane są w dodatku

((ł. 12.1).

W celu otrzymaniu interpretacji fizycznej rotacji wektora, rozpatrzymy ruch obrotowy cieczy, występujący w miejscach tworzenia się wirów. Prędkość liniowa cząstek płynu jest równa wrain ot (rys. 1.9), gdzie w jest prędkością kątową, a w postaci wektorowej

przy czym

wobec czego

rotv

v = u)X r,

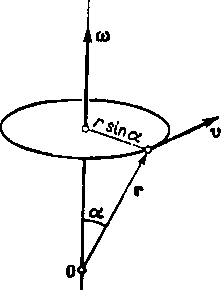
Rys. 1,9. Ruch obrotowy punktu zc stalą prędkością kątową

«! = «)_, 1,-i- fUj.l^ + to. 1.,

r = ,xl_Jt + >’l, + zl_J,

)]c

Vd    d    "I

+ — (w_yz-a>,y)~ —(a>_xy-to,x) 1,+ \_3z    ox    J

fd'    v    ,1

I g_x(“zX-w_xz)~■ (co,z-w_My) I1, =

”\j)y^y~^Wy~    ^x~⁰⁾=‘^z^ l^ +

d

dz'

=2 a>_x 1*+2W, 1, +2a), I_z—2w, przy założeniu stałej prędkości kątowej. Mamy zatem

<o=jrot v,

co oznacza, że wektor prędkości kątowej jest równy połowie rotacji wektora prędkości liniowej.

Na podstawie wzorów dla gradientu, dywergencji i rotacji wektora w układzie współrzędnych prostokątnych łatwo wykazać następujące tożsamości:

(1.29)

rot grad f» = 0, div rot A = 0.

Inne wzory są podane w dodatku. Wzory te są również prawdziwe w innych układach współrzędnych.