Image0038 BMP

<f // d/ = 2nrH,

wobec czego

iz

litr’

z, ^r^r₂.

(4.8)

W powyższym wyrażeniu r zmienia się od r_y do r₂, wobec czego natężenie pola magnetycznego we wnętrzu cewki nie jest wielkością stałą. Zazwyczaj natężenie pola magne-

. . ri+^r2

tycznego oblicza się dla tzw. średniej drogi mającej postać okręgu o promieniu r_it «»—-■■■ Średnia wartość natężenia pola magnetycznego w cewce toroidalnej wyraża się więc wzorem

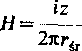
iz

n(r,+r₂)

(4.9)

Wielkość iz równą iloczynowi prądu płynącego w uzwojeniu cewki i liczby zwojów nazywamy antperozwojami cewki.

Przekład 1. Obliczymy średnią wartość natężenia pola magnetycznego we wnętrzu cewki toroidalnej, jeżeli i=lA, z= 1000, r,=9cm, r₂ = 11 cm.

Na podstawie wzoru (4,9) otrzymujemy

= 15,9 A/cm.

1000-1 A

Jt{9+ li) cm 4.2.4. Natężenie pola magnetycznego we wnętrzu cewki solenoidalnej

Na rdzeniu w kształcie walca lub graniastosłupa nawinięto równomiernie uzwojenie zawierające z zwojów (rys. 4.5), w których płynie prąd i. Gdy długość l cewki jest dostatecznie duża, wówczas można przyjąć, że w jej wnętrzu pole magnetyczne jest równomierne. Schematyczny obraz pola magnetycznego rozpatrywanej cewki przedstawiony jest na rys. 4.5. Jako drogę całkowania przy stosowaniu prawa przepływu przyjmiemy linię pola ABC A. Powierzchnię o krzywej brzegowej ABC A przenika z zwojów przewodzących prąd i, wobec czego przepływ przez tę powierzchnię jest równy amperozwpjom iz; mamy zatem

£ Hól=iz,

ABC A

Rys. 4.5. Cewka solenoidalna

filii! i j II lif '« Zi .

AM    Ml A

W obszarze na zewnątrz cewki pole magnetyczne jest bardzo słabe w porównaniu z polem w icf wnętrzu. Wskutek tego nie popełniu się dużego błędu, gdy w powyższym wyrażeniu jnmmiic się całkę J Hdl\ otrzymujemy zatem w przybliżeniu

BCA

AB

Pomijając zniekształcenie pola magnetycznego w obszarze blisko krańców cewki, mamy j H dl-III, wobec czego natężenie pola magnetycznego w dowolnym punkcie obszaru

AM

wewnętrznego cewki wyraża się wzorem    ,

iZ

f

(4.10)

Przykład 2. Obliczymy natężenie pola magnetycznego we wnętrzu cewki solenoidalnej, jeżeli i tl.s A, z -600, i = 20cm.

Nit podstawie wzoru (4.10) otrzymujemy

600-0,5 A

H—------ — =■ 15 A/cm.

20 cm

4..1 Potencjały pola magnetostatycznego

4. t.l. Potencjał skalarny

Jeżeli gęstość prądu równa się zeru w każdym punkcie pewnego obszaru, to pole magne-i ostu tyczne w tym obszarze jest bezwirowe, bowiem rot H=0. Podobnie jak w polu ełckim. Litycznym, można wówczas wprowadzić skalarny potencjał magnetyczny Y^, zwanj wpmst potencjałem magnetycznym, który jest określony w każdym punkcie tego obszaru Nu tężenie pola magnetycznego przedstawia się w postaci

H= — grad    (4.11

pi/y czym rot H=0 ze względu na tożsamość wektorową rot grad 0. Składową wek (mu 11 w kierunku osi l przedstawia wzór (por. p. 1.2.1)

dK

(4.12

dl

gdzie:    * oznacza pochodną kierunkową funkcji V„.

dl

Potencja! magnetyczny V_v spełnia równanie Laplace’a

V²P„=0

(4.13

r