Image0078 BMP

wobec czego

wobec czego

(8.55)

c

P+)Q = I*\Ę*dl.

zgodnie ze wzorem (8.54).

Po podstawieniu zależności (8.55) do wzoru (8.49), otrzymujemy wzór określający impedancję wewnętrzną odcinka przewodu

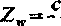
fE-di

(3.56)

bowiem 1² — H*. Wnioskujemy stąd, że impedancja wewnętrzna odcinka przewodu jest

równa ilorazowi wartości zespolonej napięcia f E • dl wzdłuż linii znajdującej się na po-

b

wierzchni tego odcinka pr2ez wartość zespoloną prądu płynącego w przewodzie.

Zależność (8.56) przyjmowana jest jako wzór określający impedancję wewnętrzną przewodu.

8.5.3. Impedancja zewnętrzna przewodu

Impedancję zewnętrzną przewodu określamy za pomocą wzoru

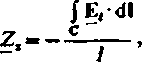
(8.57)

c

gdzie: E,jest natężeniem indukowanego pola elektrycznego (por. p. 7.1,1). Całka liniowa (Ej-dl natężenia indukowanego pola elektrycznego wzdłuż linii C przedstawia siłę elek

tromotoryczną indukowaną wzdłuż tej linii wskutek zmian czasowych zewnętrznego pola magnetycznego. Drogą całkowania całki w zależności (8.57) jest łinia C znajdująca się na powierzchni przewodu. Zgodnie z powyższym, impedancja ze wnętrzna przewodu jest równa pomnożonemu przez —1 ilorazowa wartości zespolonej siły elektromotorycznej, indukowanej w przewodzie wskutek zmian czasowych zewnętrznego pola magnetycznego, przez wartość zespoloną prądu w tym przewodzie.

W celu dokładniejszego wyjaśnieuia zagadnieuia, rozpatrzmy przewód równoległy do powierzchni ziemi, przewodzący prąd I (rys. 8.3). Rozpatrzmy prostokąt abcd, którego

Rys. 8.3. Przewód nad powierzchni4 ziemi

link ab znajduje sii; na powicr/chni przewodu (rys. 8.3). Zewnętrzny strumień magnetyczny (/>, przewodu jest równy strumieniowi magnetycznemu przez rozpatrywany prostokąt przy założeniu, że bok cd oddala się do nieskończoności. Przedstawiając ten strumień w postaci całki liniowej potencjału wektorowego A wzdłuż krzywej brzegowej powierzchni

(por. p. 4.3.2), mamy

<P_Z= lim | A-dl,

p-mo abeda

a stąd

4>_t= j A-dl + lim J A-dl,    (8.58)

ab    <)•*« cd

bowiem w rozpatrywanym układzie wektor A jest równoległy do osi przewodu, wobec i /ego całki wzdłuż boków be oraz da prostokąta są równe zeru. Można udowodnić, że granica całki w zależności (8.58 ) jest równa zeru, wobec czego

d>*= f A*dl.    (8.59)

d b

Siła elektromotoryczna indukowana w przewodzie przez zewnętrzny strumień magnetyczny jest równa

dtP,

di

e. = -

a w postaci zespolonej

(8.60^

(8.61)

l'o podstawieniu wzoru (8.59) znajdujemy

jĘrdl,

pr/y uwzględnieniu zależności E_; — — jorA. Otrzymany wynik wyjaśnia, że całka liniowa natężenia indukowanego pola elektrycznego wzdłuż linii położonej na powierzchni przewodu przedstawia siłę elektromotoryczną indukowaną w tym przewodzie przez zewnętrzne pole magnetyczne.

8.5.4. Impedancja przewodu

Różnica wartości zespolonych potencjałów skalarnych w punktach A i B przewodu / rys. 8.1 wyraża się wzorem

V_a~Vb= J    (8.62)

ADB “

gdzie: E„. jest natężeniem statycznego pola elektrycznego (por. p. 7.1.1).

Drogę całkowania między punktem A a punktem B można przyjąć zupełnie dowolnie, bowiem pole statyczne jest polem potencjalnym i rozpatrywana całka nie zależy od postaci linii łączącej te punkty. Korzystając z tej dowolności, jako drogę całkowania przyjmujemy linię ADB na powierzchni przewodu, co jest zaznaczone w zapisie wzoru (8.62).

Do zależności (8.62) podstawiamy

E.,=E—E„